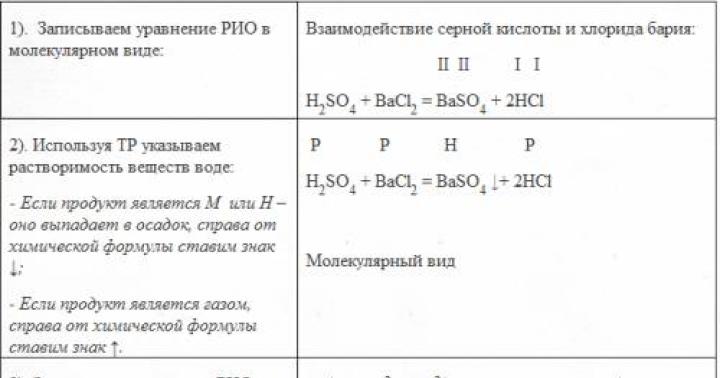
На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (обладают одной и той же плотностью вероятностей).

Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероят­ности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение.

Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в ], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f (х) имеет следующий вид:

Иногда это распределение называют законом равномерной плотности . Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.

Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то

откуда с =1/(b - a ).

Теперь функцию f (x ) можно представить в виде

Построим функцию распределения F (x ), для чего найдем выражение F (x ) на интервале [ a , b ]:

Графики функций f (x ) и F (x ) имеют вид:

Найдем числовые характеристики.

Используя формулу для вычисления математического ожидания НСВ, имеем:

Таким образом, математическое ожидание случайной вели­чины, равномерно распределенной на отрезке [ a , b ] совпадает с серединой этого отрезка.

Найдем дисперсию равномерно распределенной случайной величины:

откуда сразу же следует, что среднее квадратическое отклонение:

Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (a , b ) , принадлежащий целиком отрезку [ a , b ]:

Геометрически эта вероятность представляетсобойплощадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.

Пример1. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 минут. Найти вероятность того, что пассажир, подошедший к остановке. Будет ожидать очередной автобус менее 3 минут.

Решение:

СВ- время ожидания автобуса имеет равномерное распределение. Тогда искомая вероятность будет равна:

Пример2. Ребро куба х измерено приближенно. Причем

Рассматривая ребро куба как случайную величину, распределенную равномерно в интервале (a , b ) , найти математическое ожидание и дисперсию объема куба.

Решение:

Объем куба- случайная величина, определяемая выражением У= Х 3 . Тогда математическое ожидание равно:

Дисперсия:

Онлайн сервис:

С помощью которого моделируются многие реальные процессы. И самый такой распространённый пример – это график движения общественного транспорта. Предположим, что некий автобус (троллейбус / трамвай) ходит с интервалом в 10 минут, и вы в случайный момент времени подошли к остановке. Какова вероятность того, что автобус подойдёт в течение 1 минуты? Очевидно, 1/10-я. А вероятность того, что придётся ждать 4-5 минут? Тоже . А вероятность того, что автобус придётся ждать более 9 минут? Одна десятая!

Рассмотрим некоторый конечный промежуток, пусть для определённости это будет отрезок . Если случайная величина обладает постоянной плотностью распределения вероятностей на данном отрезке и нулевой плотностью вне него, то говорят, что она распределена равномерно . При этом функция плотности будет строго определённой:

И в самом деле, если длина отрезка (см. чертёж) составляет , то значение неизбежно равно – дабы получилась единичная площадь прямоугольника, и было соблюдено известное свойство :


Проверим его формально:
, ч.т.п. С вероятностной точки зрения это означает, что случайная величина достоверно примет одно из значений отрезка …, эх, становлюсь потихоньку занудным старикашкой =)

Суть равномерности состоит в том, что какой бы внутренний промежуток фиксированной длины мы ни рассмотрели (вспоминаем «автобусные» минуты) – вероятность того, что случайная величина примет значение из этого промежутка будет одной и той же. На чертеже я заштриховал троечку таких вероятностей – ещё раз заостряю внимание, что они определяются площадями , а не значениями функции !

Рассмотрим типовое задание:

Пример 1

Непрерывная случайная величина задана своей плотностью распределения:

Найти константу , вычислить и составить функцию распределения. Построить графики . Найти

Иными словами, всё, о чём только можно было мечтать:)

Решение : так как на интервале (конечном промежутке) , то случайная величина имеет равномерное распределение, и значение «цэ» можно отыскать по прямой формуле . Но лучше общим способом – с помощью свойства:

…почему лучше? Чтобы не было лишних вопросов;)

Таким образом, функция плотности:

Выполним чертёж. Значения невозможны , и поэтому жирные точки ставятся внизу:


В качестве экспресс-проверки вычислим площадь прямоугольника:
, ч.т.п.

Найдём математическое ожидание , и, наверное, вы уже догадываетесь, чему оно равно. Вспоминаем «10-минутный» автобус: если случайным образом подходить к остановке много-много дней упаси, то в среднем его придётся ждать 5 минут.

Да, именно так – матожидание должно находиться ровно посерединке «событийного» промежутка:
, как и предполагалось.

Дисперсию вычислим по формуле . И вот тут нужен глаз да глаз при вычислении интеграла:

Таким образом, дисперсия :

Составим функцию распределения . Здесь ничего нового:

1) если , то и ;

2) если , то и:

3) и, наконец, при , поэтому:

В результате:

Выполним чертёж:


На «живом» промежутке функция распределения растёт линейно , и это ещё один признак, что перед нами равномерно распределённая случайная величина. Ну, ещё бы, ведь производная линейной функции – есть константа.

Требуемую вероятность можно вычислить двумя способами, с помощью найденной функции распределения:

либо с помощью определённого интеграла от плотности:

Кому как нравится.

И здесь ещё можно записать ответ : ,
, графики построены по ходу решения.

…«можно», потому что за его отсутствие обычно не карают. Обычно;)

Для вычисления и равномерной случайной величины существуют специальные формулы, которые я предлагаю вам вывести самостоятельно:

Пример 2

Непрерывная случайная величина задана плотностью .

Вычислить математическое ожидание и дисперсию. Результаты максимально упростить (формулы сокращённого умножения в помощь) .

Полученные формулы удобно использовать для проверки, в частности, проверьте только что прорешанную задачу, подставив в них конкретные значения «а» и «б». Краткое решение внизу страницы.

И в заключение урока мы разберём парочку «текстовых» задач:

Пример 3

Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляются до ближайшего целого деления. Считая, что погрешности округлений распределены равномерно, найти вероятность того, что при очередном измерении она не превзойдёт 0,04.

Для лучшего понимания решения представим, что это какой-нибудь механический прибор со стрелкой, например, весы с ценой деления 0,2 кг, и нам предстоит взвесить кота в мешке. Но не в целях выяснить его упитанность – сейчас будет важно, ГДЕ между двумя соседними делениями остановится стрелка.

Рассмотрим случайную величину – расстояние стрелки от ближайшего левого деления. Или от ближайшего правого, это не принципиально.

Составим функцию плотности распределения вероятностей:

1) Так как расстояние не может быть отрицательным, то на интервале . Логично.

2) Из условия следует, что стрелка весов с равной вероятностью может остановиться в любом месте между делениями* , включая сами деления, и поэтому на промежутке :

* Это существенное условие. Так, например, при взвешивании кусков ваты или килограммовых пачек соли равномерность будет соблюдаться на куда более узких промежутках.

3) И поскольку расстояние от БЛИЖАЙШЕГО левого деления не может быть больше, чем 0,2, то при тоже равна нулю.

Таким образом:

Следует отметить, что о функции плотности нас никто не спрашивал, и её полное построения я привёл исключительно в познавательных цепях. При чистовом оформлении задачи достаточно записать только 2-й пункт.

Теперь ответим на вопрос задачи. Когда погрешность округления до ближайшего деления не превзойдёт 0,04? Это произойдёт тогда, когда стрелка остановится не далее чем на 0,04 от левого деления справа или не далее чем на 0,04 от правого деления слева . На чертеже я заштриховал соответствующие площади:

Осталось найти эти площади с помощью интегралов . В принципе, их можно вычислить и «по-школьному» (как площади прямоугольников), но простота не всегда находит понимание;)

По теореме сложения вероятностей несовместных событий :

– вероятность того, что ошибка округления не превзойдёт 0,04 (40 грамм для нашего примера)

Легко понять, что максимально возможная погрешность округления составляет 0,1 (100 грамм) и поэтому вероятность того, что ошибка округления не превзойдёт 0,1 равна единице. И из этого, кстати, следует другой, более лёгкий способ решения, в котором нужно рассмотреть случайную величину – погрешность округления до ближайшего деления . Но первый способ мне пришёл в голову первым:)

Ответ : 0,4

И ещё один момент по задаче . В условии речь может идти о погрешностях не округлений , а о случайных погрешностях самих измерений , которые, как правило (но не всегда) , распределены по нормальному закону . Таким образом, всего лишь одно слово может в корне изменить решение! Будьте начеку и вникайте в смысл задач!

И коль скоро всё идёт по кругу, то ноги нас приносят на ту же остановку:

Пример 4

Автобусы некоторого маршрута идут строго по расписанию и интервалом 7 минут. Составить функцию плотности случайной величины – времени ожидании очередного автобуса пассажиром, который наудачу подошёл к остановке. Найти вероятность того, что он будет ждать автобус не более трёх минут. Найти функцию распределения и пояснить её содержательный смысл.

Равномерным распределением называют такое распределение случайной величины, когда она с одинаковой вероятностью может принимать любое значение в заданных пределах.

Равномерное распределение случайной величины показано на рис. 5.9.

Рис. 5.9.

Плотность вероятности равномерного распределения имеет вид:

где а и Ь - параметры закона, определяющие пределы изменения случайной величины X.

Закону равномерного распределения подчиняются, в частности, погрешности от трения в опорах приборов, неисключенные остатки систематических погрешностей, погрешности дискретности в цифровых приборах, погрешности размеров в пределах одной группы сортировки при селективной сборке, погрешности параметров изделий, отобранных в более узких пределах, по сравнению с технологическим допуском, суммарная погрешность обработки, вызван-

Интеграл

носит название нормированной функции Лапласа, а его значения для х - X различных / = --табулированы. Значение нормированной функции Лапласа Ф(/) с погрешностью менее Ю"5 можно определить по формуле

Если / >0, Ф(/) = 7", а если / < 0, то Ф(/) = 1-7". Функция Лапласа нечетная, т. е.

Для отрицательных значений /табличные данные берутся со знаком минус.

Вероятность того, что случайная величина, подчиняющаяся закону нормального распределения, при измерениях примет значение в пределах (х, х,), можно записать через Ф(/) следующим образом:

У теоретической кривой нормального распределения ветви ее асимптотически приближаются к оси абсцисс, т. е. зона рассеивания случайной величины х лежит в пределах ±оо. Практически зона рассеивания случайной величины х ограничена конечными пределами.

Например, вероятность того, что случайная величина будет находиться в пределах

линейным изменением во времени доминирующего фактора (износ режущего инструмента, температурная деформация и т. д.), погрешности, возникающие за счет округления величин, полученных при измерении на приборах, и др.

Функция распределения F(x) равномерного распределения (интегральная функция распределения) выражается следующим уравнением для (а < х < Ь):

Вид функции распределения показан на рис. 5.10.

Математическое ожидание Л/(х), дисперсия 0(х) и среднее квадратичное отклонение (а) случайной величины, подчиняющейся равномерному распределению, соответственно равны:

Практически предельное поле рассеивания со при равномерном распределении равно Ь - а или с учетом (5.48), т. е.

со = Ь - а = 2т/Зет.

Рис. 5.10.

Рис. 5.11.

Закон Симпсона

Вид кривой треугольного распределения показан на рис. 5.11. Плотность вероятности имеет вид:

По этому закону распределены, например, погрешности суммы (разности) двух равномерно распределенных величин. Если, например, отклонения размеров отверстия и вала распределены в пределах полей допусков равномерно, а допуски вала и отверстия примерно одинаковые, то зазоры в пределах допуска зазора будут распределены по закону треугольника. Плотность вероятности зазоров при этом будет иметь следующий вид:

где 5т(п, 5^ - соответственно минимальное и максимальное значения зазора в соединении; .$т = ^"^^"ла _ среднее значение зазора в соединении; /Г5 = 5т1п - допуск зазора; л - текущее значение зазора.

Функция распределения закона Симпсона имеет вид:

Графическое представление интегральной функции распределения приведено на рис. 5.12.

Математическое ожидание, дисперсия и среднее квадратичное отклонение случайной величины, подчиняющейся закону Симпсона, соответственно равны:

Практически предельное поле рассеивания сопри распределении случайной величины по закону Симпсона равно 2/, т. е.

В качестве примера непрерывной случайной величины рассмотрим случайную величину X, равномерно распределенную на интервале (a; b). Говорят, что случайная величина X равномерно распределена на промежутке (a; b), если ее плотность распределения непостоянна на этом промежутке:

Из условия нормировки определим значение константы c . Площадь под кривой плотности распределения должна быть равна единице, но в нашем случае - это площадь прямоугольника с основанием (b - α) и высотой c (рис. 1).

Рис. 1 Плотность равномерного распределения
Отсюда находим значение постоянной c:

Итак, плотность равномерно распределенной случайной величины равна

Найдем теперь функцию распределения по формуле:
1) для
2) для
3) для 0+1+0=1.
Таким образом,

Функция распределения непрерывна и не убывает (рис. 2).

Рис. 2 Функция распределения равномерно распределенной случайной величины

Найдем математическое ожидание равномерно распределенной случайной величины по формуле:

Дисперсия равномерного распределения рассчитывается по формуле и равна

Пример №1 . Цена деления шкалы измерительного прибора равна 0.2 . Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0.04 ; б) большая 0.02
Решение. Ошибка округления есть случайная величина, равномерно распределенная на промежутке между соседними целыми делениями. Рассмотрим в качестве такого деления интервал (0; 0,2) (рис. а). Округление может проводиться как в сторону левой границы - 0, так и в сторону правой - 0,2, значит, ошибка, менее либо равная 0,04, может быть сделана два раза, что необходимо учесть при подсчете вероятности:



P = 0,2 + 0,2 = 0,4

Для второго случая величина ошибки может превышать 0,02 также с обеих границ деления, то есть она может быть либо больше 0,02, либо меньше 0,18.


Тогда вероятность появления такой ошибки:

Пример №2 . Предполагалось, что о стабильности экономической обстановки в стране (отсутствии войн, стихийных бедствий и т. д.) за последние 50 лет можно судить по характеру распределения населения по возрасту: при спокойной обстановке оно должно быть равномерным . В результате проведенного исследования, для одной из стран были получены следующие данные.

Имеются ли основания полагать, что в стране была нестабильная обстановка?

Решение проводим с помощью калькулятора Проверка гипотез . Таблица для расчета показателей.

Группы	Середина интервала, x i	Кол-во, f i	x i * f i	Накопленная частота, S	|x - x ср |*f	(x - x ср) 2 *f	Частота, f i /n
0 - 10	5	0.14	0.7	0.14	5.32	202.16	0.14
10 - 20	15	0.09	1.35	0.23	2.52	70.56	0.09
20 - 30	25	0.1	2.5	0.33	1.8	32.4	0.1
30 - 40	35	0.08	2.8	0.41	0.64	5.12	0.08
40 - 50	45	0.16	7.2	0.57	0.32	0.64	0.16
50 - 60	55	0.13	7.15	0.7	1.56	18.72	0.13
60 - 70	65	0.12	7.8	0.82	2.64	58.08	0.12
70 - 80	75	0.18	13.5	1	5.76	184.32	0.18
		1	43		20.56	572	1

Показатели центра распределения .
Средняя взвешенная


Показатели вариации .
Абсолютные показатели вариации .
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = X max - X min
R = 70 - 0 = 70
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).


Среднее квадратическое отклонение .

Каждое значение ряда отличается от среднего значения 43 не более, чем на 23.92
Проверка гипотез о виде распределения .
4. Проверка гипотезы о равномерном распределении генеральной совокупности.
Для того чтобы проверить гипотезу о равномерном распределении X,т.е. по закону: f(x) = 1/(b-a) в интервале (a,b)
надо:
1. Оценить параметры a и b - концы интервала, в котором наблюдались возможные значения X, по формулам (через знак * обозначены оценки параметров):

2. Найти плотность вероятности предполагаемого распределения f(x) = 1/(b * - a *)
3. Найти теоретические частоты:
n 1 = nP 1 = n = n*1/(b * - a *)*(x 1 - a *)
n 2 = n 3 = ... = n s-1 = n*1/(b * - a *)*(x i - x i-1)
n s = n*1/(b * - a *)*(b * - x s-1)
4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы k = s-3, где s - число первоначальных интервалов выборки; если же было произведено объединение малочисленных частот, следовательно, и самих интервалов, то s - число интервалов, оставшихся после объединения.

Решение:
1. Найдем оценки параметров a * и b * равномерного распределения по формулам:


2. Найдем плотность предполагаемого равномерного распределения:
f(x) = 1/(b * - a *) = 1/(84.42 - 1.58) = 0.0121
3. Найдем теоретические частоты:
n 1 = n*f(x)(x 1 - a *) = 1 * 0.0121(10-1.58) = 0.1
n 8 = n*f(x)(b * - x 7) = 1 * 0.0121(84.42-70) = 0.17
Остальные n s будут равны:
n s = n*f(x)(x i - x i-1)

i	n i	n * i	n i - n * i	(n i - n* i) 2	(n i - n * i) 2 /n * i
1	0.14	0.1	0.0383	0.00147	0.0144
2	0.09	0.12	-0.0307	0.000943	0.00781
3	0.1	0.12	-0.0207	0.000429	0.00355
4	0.08	0.12	-0.0407	0.00166	0.0137
5	0.16	0.12	0.0393	0.00154	0.0128
6	0.13	0.12	0.0093	8.6E-5	0.000716
7	0.12	0.12	-0.000701	0	4.0E-6
8	0.18	0.17	0.00589	3.5E-5	0.000199
Итого	1				0.0532

Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение K набл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: }