|
Το πρώτο αξιοσημείωτο όριο. Η εξαγωγή του πρώτου αξιοσημείωτου ορίου παρουσιάζει ενδιαφέρον από την άποψη της εφαρμογής της θεωρίας των ορίων και ως εκ τούτου σας την προσφέρουμε σχεδόν στο σύνολό της. Ας εξετάσουμε τη συμπεριφορά της συνάρτησης |
στο 
. Για να το κάνετε αυτό, θεωρήστε έναν κύκλο ακτίνας 1. ας υποδηλώσουμε την κεντρική γωνία του MOB με Χ, όπου 
.Τότε ξεκάθαρα η περιοχή DMOA< площадь сектора МОА < площадьDСОА (см. рис. 1).
S D MOA = 
S MOA = 
=
S D C OA = 
Επιστρέφοντας στην αναφερόμενη ανισότητα και διπλασιάζοντάς την, παίρνουμε:
αμαρτία Χ < Χ < tg Χ.
Μετά διαίρεση κατά όρο αμαρτία Χ:
ή 
Επειδή η 
, μετά τη μεταβλητή 
συνάπτεται μεταξύ δύο ποσοτήτων που έχουν το ίδιο όριο, δηλ. , με βάση το θεώρημα για το όριο της ενδιάμεσης συνάρτησης της προηγούμενης παραγράφου, έχουμε:
-πρώτο υπέροχο όριο .
Παράδειγμα.Υπολογίστε τα όρια των συναρτήσεων χρησιμοποιώντας το πρώτο αξιοσημείωτο όριο:
Απάντηση. 1) 1, 2) 0, 3)
Ασκηση:Υπολογίστε το όριο μιας συνάρτησης χρησιμοποιώντας το πρώτο αξιοσημείωτο όριο:
Απάντηση: -2.
Το δεύτερο αξιοσημείωτο όριο.
Για να εξαχθεί το δεύτερο αξιοσημείωτο όριο, εισάγουμε τον ορισμό του αριθμού μι:
Ορισμός.
Μεταβλητό Όριο 
στο 
κάλεσε έναν αριθμόμι
:
- Δεύτερο υπέροχο όριο
Αριθμός μι– παράλογος αριθμός. Η τιμή του σε δέκα αληθινά δεκαδικά ψηφία συνήθως στρογγυλοποιείται σε ένα πραγματικό δεκαδικό ψηφίο:
μι= 2,7182818284..."2,7.
Θεώρημα. Λειτουργία 
στοΧ
τείνει στο άπειρο, τείνει στο όριομι
:
Παράδειγμα.Υπολογίστε τα όρια των συναρτήσεων:
Λύση.
Σύμφωνα με τις ιδιότητες των ορίων, το όριο του βαθμού είναι ίσο με το βαθμό του ορίου, δηλαδή:
Επιπλέον, με παρόμοιο τρόπο μπορεί να αποδειχθεί ότι 
Απάντηση. 1)μι 3 , 2)μι 2 , 3)μι 4 .
Ασκηση.Υπολογίστε το όριο της συνάρτησης χρησιμοποιώντας το δεύτερο αξιοσημείωτο όριο:
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ΣΧΕΤΙΚΑ ΜΕ 
απάντηση: ε -5
Συνέχεια συνάρτησης Συνέχεια συνάρτησης σε σημείο
Ορισμός. Λειτουργίαφά ( Χ ), Χ Î ( ένα ; σι ) Χ Ο Î ( ένα ; σι ), αν το όριο της συνάρτησηςφά ( Χ ) στο σημείοΧ Ο υπάρχει και ισούται με την τιμή της συνάρτησης σε αυτό το σημείο:
.
Σύμφωνα με αυτόν τον ορισμό, η συνέχεια της συνάρτησης φά(Χ) στο σημείο Χ Οσημαίνει ότι πληρούνται οι ακόλουθες προϋποθέσεις:
λειτουργία φά(Χ) πρέπει να οριστεί στο σημείο Χ Ο ;
συνάρτηση y φά(Χ) πρέπει να υπάρχει ένα όριο στο σημείο Χ Ο ;
όριο μιας συνάρτησης φά(Χ) στο σημείο Χ Οπρέπει να ταιριάζει με την τιμή της συνάρτησης σε αυτό το σημείο.
Παράδειγμα.
Λειτουργία φά(Χ)
=
Χ 2
ορίζεται σε ολόκληρη την αριθμητική γραμμή και συνεχίζεται σε ένα σημείο Χ= 1 γιατί φά( 1)
= 1 και 
Συνέχεια μιας συνάρτησης σε ένα σύνολο
Ορισμός. Λειτουργίαf(x), λέγεται συνεχής στο διάστημα(α; β), αν είναι συνεχής σε κάθε σημείο αυτού του διαστήματος.
Εάν μια συνάρτηση είναι συνεχής σε κάποιο σημείο, τότε αυτό το σημείο ονομάζεται σημείο συνέχειας αυτής της συνάρτησης. Σε περιπτώσεις όπου το όριο μιας συνάρτησης σε ένα δεδομένο σημείο δεν υπάρχει ή η τιμή της δεν συμπίπτει με την τιμή της συνάρτησης σε ένα δεδομένο σημείο, τότε η συνάρτηση ονομάζεται ασυνεχής σε αυτό το σημείο και το ίδιο το σημείο ονομάζεται ασυνέχεια σημείο της συνάρτησης f(x).
Ιδιότητες συνεχών συναρτήσεων.
1) Το άθροισμα ενός πεπερασμένου αριθμού συναρτήσεων συνεχών σε ένα σημείο ΕΝΑ,
2) Γινόμενο πεπερασμένου αριθμού συναρτήσεων συνεχών σε ένα σημείο ΕΝΑ,υπάρχει μια συνάρτηση που είναι συνεχής σε αυτό το σημείο.
3) Ο λόγος ενός πεπερασμένου αριθμού συναρτήσεων συνεχούς σε ένα σημείο ΕΝΑ,είναι μια συνάρτηση που είναι συνεχής σε αυτό το σημείο εάν η τιμή της συνάρτησης στον παρονομαστή είναι διαφορετική από το μηδέν στο σημείο ΕΝΑ.
Παράδειγμα.
Λειτουργία φά(Χ) = Χ Π, Οπου n Î Ν, είναι συνεχής σε ολόκληρη την αριθμητική γραμμή. Αυτό το γεγονός μπορεί να αποδειχθεί χρησιμοποιώντας την ιδιότητα 2 και τη συνέχεια της συνάρτησης φά(Χ) = Χ.
Λειτουργία φά(Χ) = sΧ Π (Με– σταθερά) είναι συνεχής σε ολόκληρη την αριθμητική γραμμή, με βάση την ιδιότητα 2 και το παράδειγμα 1.
Θεώρημα 1. Ένα πολυώνυμο είναι μια συνάρτηση που είναι συνεχής σε ολόκληρη την αριθμητική γραμμή.
Θεώρημα 2 . Οποιαδήποτε κλασματική ορθολογική συνάρτηση είναι συνεχής σε κάθε σημείο του πεδίου ορισμού της.
Παράδειγμα.
Ορισμός
Λειτουργίαφά
(
Χ
)
ονομάζεται συνεχής σε ένα σημείοx = α
, εάν σε αυτό το σημείο η προσαύξησή του 
τείνει στο μηδέν όταν το όρισμα αυξάνεται 
τείνει στο μηδέν, ή με άλλα λόγια: συνάρτησηφά
(Χ)
ονομάζεται συνεχής σε ένα σημείοx = α
, εάν σε αυτό το σημείο μια απειροελάχιστη αύξηση του ορίσματος αντιστοιχεί σε μια απειροελάχιστη αύξηση της συνάρτησης, δηλ. 
Υπάρχουν αρκετά αξιόλογα όρια, αλλά τα πιο διάσημα είναι το πρώτο και το δεύτερο αξιοσημείωτα όρια. Το αξιοσημείωτο με αυτά τα όρια είναι ότι χρησιμοποιούνται ευρέως και με τη βοήθειά τους μπορεί κανείς να βρει άλλα όρια που συναντώνται σε πολλά προβλήματα. Αυτό θα κάνουμε στο πρακτικό μέρος αυτού του μαθήματος. Για να λύσουμε προβλήματα μειώνοντάς τα στο πρώτο ή το δεύτερο αξιοσημείωτο όριο, δεν χρειάζεται να αποκαλύψουμε τις αβεβαιότητες που περιέχονται σε αυτά, καθώς οι τιμές αυτών των ορίων έχουν από καιρό συναχθεί από μεγάλους μαθηματικούς.
Το πρώτο υπέροχο όριοονομάζεται το όριο της αναλογίας του ημιτονοειδούς ενός απειροελάχιστου τόξου προς το ίδιο τόξο, εκφρασμένο σε ακτινικό μέτρο:
Ας προχωρήσουμε στην επίλυση προβλημάτων στο πρώτο αξιοσημείωτο όριο. Σημείωση: εάν υπάρχει μια τριγωνομετρική συνάρτηση κάτω από το πρόσημο ορίου, αυτό είναι ένα σχεδόν σίγουρο σημάδι ότι αυτή η έκφραση μπορεί να μειωθεί στο πρώτο αξιοσημείωτο όριο.
Παράδειγμα 1.Βρείτε το όριο.
Λύση. Αντικατάσταση ΧΤο μηδέν οδηγεί σε αβεβαιότητα:
.
Ο παρονομαστής είναι ημίτονο, επομένως, η έκφραση μπορεί να φτάσει στο πρώτο αξιοσημείωτο όριο. Ας ξεκινήσουμε τη μεταμόρφωση:
.
Ο παρονομαστής είναι το ημίτονο των τριών Χ, αλλά ο αριθμητής έχει μόνο ένα Χ, που σημαίνει ότι πρέπει να πάρετε τρία Χ στον αριθμητή. Για τι? Εισαγωγή 3 Χ = ένακαι πάρτε την έκφραση.
Και φτάνουμε σε μια παραλλαγή του πρώτου αξιοσημείωτου ορίου:
γιατί δεν έχει σημασία ποιο γράμμα (μεταβλητή) σε αυτόν τον τύπο βρίσκεται αντί του X.
Πολλαπλασιάζουμε το Χ επί τρία και αμέσως διαιρούμε:
.
Σύμφωνα με το πρώτο αξιοσημείωτο όριο που παρατηρήσαμε, αντικαθιστούμε την κλασματική έκφραση:
Τώρα μπορούμε επιτέλους να λύσουμε αυτό το όριο:
.
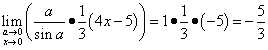Παράδειγμα 2.Βρείτε το όριο.
Λύση. Η άμεση αντικατάσταση οδηγεί και πάλι στην αβεβαιότητα «μηδέν διαιρούμενο με μηδέν»:
.
Για να λάβετε το πρώτο αξιοσημείωτο όριο, είναι απαραίτητο το x κάτω από το ημιτονικό πρόσημο στον αριθμητή και μόνο το x στον παρονομαστή να έχουν τον ίδιο συντελεστή. Έστω αυτός ο συντελεστής ίσος με 2. Για να το κάνετε αυτό, φανταστείτε τον τρέχοντα συντελεστή για το x όπως παρακάτω, εκτελώντας πράξεις με κλάσματα, λαμβάνουμε:
.
Παράδειγμα 3.Βρείτε το όριο.
Λύση. Κατά την αντικατάσταση, παίρνουμε και πάλι την αβεβαιότητα «μηδέν διαιρούμενο με μηδέν»:
.
Πιθανότατα έχετε ήδη καταλάβει ότι από την αρχική έκφραση μπορείτε να πάρετε το πρώτο υπέροχο όριο πολλαπλασιασμένο με το πρώτο υπέροχο όριο. Για να γίνει αυτό, αποσυνθέτουμε τα τετράγωνα του x στον αριθμητή και του ημιτόνου στον παρονομαστή σε πανομοιότυπους συντελεστές και για να πάρουμε τους ίδιους συντελεστές για το x και το ημίτονο, διαιρούμε το x στον αριθμητή με το 3 και αμέσως πολλαπλασιάζουμε κατά 3. Παίρνουμε:
.
Παράδειγμα 4.Βρείτε το όριο.
Λύση. Για άλλη μια φορά παίρνουμε την αβεβαιότητα «μηδέν διαιρούμενο με μηδέν»:
.
Μπορούμε να λάβουμε την αναλογία των δύο πρώτων αξιοσημείωτων ορίων. Διαιρούμε και τον αριθμητή και τον παρονομαστή με το x. Έπειτα, έτσι ώστε οι συντελεστές για ημίτονο και xes να συμπίπτουν, πολλαπλασιάζουμε το ανώτερο x με 2 και αμέσως διαιρούμε με 2, και πολλαπλασιάζουμε το χαμηλότερο x με 3 και αμέσως διαιρούμε με 3. Παίρνουμε:
Παράδειγμα 5.Βρείτε το όριο.
Λύση. Και πάλι η αβεβαιότητα του «μηδέν διαιρούμενο με το μηδέν»:
Θυμόμαστε από την τριγωνομετρία ότι η εφαπτομένη είναι η αναλογία του ημιτόνου προς το συνημίτονο, και το συνημίτονο του μηδενός είναι ίσο με ένα. Πραγματοποιούμε τους μετασχηματισμούς και παίρνουμε:
.
Παράδειγμα 6.Βρείτε το όριο.
Λύση. Η τριγωνομετρική συνάρτηση κάτω από το πρόσημο ενός ορίου προτείνει και πάλι τη χρήση του πρώτου αξιοσημείωτου ορίου. Το παριστάνουμε ως την αναλογία ημιτόνου προς συνημίτονο.
Το πρώτο αξιοσημείωτο όριο είναι η ακόλουθη ισότητα:
\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(εξίσωση)
Εφόσον για $\alpha\to(0)$ έχουμε $\sin\alpha\to(0)$, λένε ότι το πρώτο αξιοσημείωτο όριο αποκαλύπτει μια αβεβαιότητα της μορφής $\frac(0)(0)$. Γενικά, στον τύπο (1), αντί για τη μεταβλητή $\alpha$, οποιαδήποτε έκφραση μπορεί να τοποθετηθεί κάτω από το ημιτονικό πρόσημο και στον παρονομαστή, αρκεί να πληρούνται δύο προϋποθέσεις:
- Οι εκφράσεις κάτω από το ημιτονικό πρόσημο και στον παρονομαστή τείνουν ταυτόχρονα στο μηδέν, δηλ. υπάρχει αβεβαιότητα της μορφής $\frac(0)(0)$.
- Οι εκφράσεις κάτω από το ημιτονικό και στον παρονομαστή είναι ίδιες.
Συχνά χρησιμοποιούνται επίσης συμπεράσματα από το πρώτο αξιοσημείωτο όριο:
\αρχή(εξίσωση) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(εξίσωση) \begin(εξίσωση) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(εξίσωση) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end (εξίσωση)
Έντεκα παραδείγματα επιλύονται σε αυτήν τη σελίδα. Το Παράδειγμα Νο. 1 είναι αφιερωμένο στην απόδειξη των τύπων (2)-(4). Τα παραδείγματα Νο. 2, Νο. 3, Νο. 4 και Νο. 5 περιέχουν λύσεις με λεπτομερή σχόλια. Τα Παραδείγματα Νο. 6-10 περιέχουν λύσεις χωρίς ουσιαστικά σχόλια, επειδή δόθηκαν λεπτομερείς εξηγήσεις σε προηγούμενα παραδείγματα. Η λύση χρησιμοποιεί ορισμένους τριγωνομετρικούς τύπους που μπορούν να βρεθούν.
Επιτρέψτε μου να σημειώσω ότι η παρουσία τριγωνομετρικών συναρτήσεων σε συνδυασμό με την αβεβαιότητα $\frac (0) (0)$ δεν σημαίνει απαραίτητα την εφαρμογή του πρώτου αξιοσημείωτου ορίου. Μερικές φορές απλοί τριγωνομετρικοί μετασχηματισμοί είναι επαρκείς - για παράδειγμα, βλ.
Παράδειγμα Νο. 1
Αποδείξτε ότι $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
α) Εφόσον $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, τότε:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
Εφόσον $\lim_(\alpha\to(0))\cos(0)=1$ και $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$, Οτι:
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$
β) Ας κάνουμε την αλλαγή $\alpha=\sin(y)$. Αφού $\sin(0)=0$, τότε από τη συνθήκη $\alpha\to(0)$ έχουμε $y\to(0)$. Επιπλέον, υπάρχει μια γειτονιά του μηδενός στην οποία $\arcsin\alpha=\arcsin(\sin(y))=y$, άρα:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$
Η ισότητα $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ έχει αποδειχθεί.
γ) Ας κάνουμε την αντικατάσταση $\alpha=\tg(y)$. Εφόσον $\tg(0)=0$, τότε οι συνθήκες $\alpha\to(0)$ και $y\to(0)$ είναι ισοδύναμες. Επιπλέον, υπάρχει μια γειτονιά του μηδενός στην οποία $\arctg\alpha=\arctg\tg(y))=y$, επομένως, με βάση τα αποτελέσματα του σημείου α), θα έχουμε:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
Η ισότητα $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ έχει αποδειχθεί.
Οι ισότητες α), β), γ) χρησιμοποιούνται συχνά μαζί με το πρώτο αξιοσημείωτο όριο.
Παράδειγμα Νο. 2
Υπολογίστε το όριο $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4) ( x+7))$.
Αφού $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ και $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, π.χ. και ο αριθμητής και ο παρονομαστής του κλάσματος τείνουν ταυτόχρονα στο μηδέν, τότε εδώ έχουμε να κάνουμε με μια αβεβαιότητα της μορφής $\frac(0)(0)$, δηλ. Έγινε. Επιπλέον, είναι σαφές ότι οι εκφράσεις κάτω από το ημιτονικό πρόσημο και στον παρονομαστή συμπίπτουν (δηλαδή, και ικανοποιείται):
Επομένως, πληρούνται και οι δύο προϋποθέσεις που αναφέρονται στην αρχή της σελίδας. Από αυτό προκύπτει ότι ο τύπος είναι εφαρμόσιμος, δηλ. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7 ))=1$.
Απάντηση: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.
Παράδειγμα Νο. 3
Βρείτε $\lim_(x\to(0))\frac(\sin(9x))(x)$.
Εφόσον $\lim_(x\to(0))\sin(9x)=0$ και $\lim_(x\to(0))x=0$, τότε έχουμε να κάνουμε με μια αβεβαιότητα της μορφής $\frac (0 )(0)$, δηλ. Έγινε. Ωστόσο, οι εκφράσεις κάτω από το ημιτονικό πρόσημο και στον παρονομαστή δεν συμπίπτουν. Εδώ πρέπει να προσαρμόσετε την έκφραση στον παρονομαστή στην επιθυμητή μορφή. Χρειαζόμαστε η έκφραση $9x$ να είναι στον παρονομαστή, τότε θα γίνει αληθής. Ουσιαστικά, μας λείπει ένας παράγοντας 9$ στον παρονομαστή, που δεν είναι και τόσο δύσκολο να εισαχθεί—απλώς πολλαπλασιάστε την έκφραση στον παρονομαστή επί 9$. Φυσικά, για να αντισταθμίσετε τον πολλαπλασιασμό με 9$, θα πρέπει να διαιρέσετε αμέσως με 9$:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$
Τώρα οι εκφράσεις στον παρονομαστή και κάτω από το ημιτονικό σύμβολο συμπίπτουν. Και οι δύο προϋποθέσεις για το όριο $\lim_(x\to(0))\frac(\sin(9x))(9x)$ ικανοποιούνται. Επομένως, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. Και αυτό σημαίνει ότι:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Απάντηση: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Παράδειγμα αρ. 4
Βρείτε $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.
Επειδή $\lim_(x\to(0))\sin(5x)=0$ και $\lim_(x\to(0))\tg(8x)=0$, εδώ έχουμε να κάνουμε με αβεβαιότητα της φόρμας $\frac(0)(0)$. Ωστόσο, η μορφή του πρώτου αξιοσημείωτου ορίου παραβιάζεται. Ένας αριθμητής που περιέχει $\sin(5x)$ απαιτεί παρονομαστή $5x$. Σε αυτήν την περίπτωση, ο ευκολότερος τρόπος είναι να διαιρέσετε τον αριθμητή με $5x$ και να πολλαπλασιάσετε αμέσως με $5x$. Επιπλέον, θα εκτελέσουμε μια παρόμοια πράξη με τον παρονομαστή, πολλαπλασιάζοντας και διαιρώντας το $\tg(8x)$ με το $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\αριστερά|\frac(0)(0)\δεξιά| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
Μειώνοντας κατά $x$ και λαμβάνοντας τη σταθερά $\frac(5)(8)$ εκτός του ορίου, παίρνουμε:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Σημειώστε ότι το $\lim_(x\to(0))\frac(\sin(5x))(5x)$ ικανοποιεί πλήρως τις απαιτήσεις για το πρώτο αξιοσημείωτο όριο. Για να βρείτε $\lim_(x\to(0))\frac(\tg(8x))(8x)$ ισχύει ο ακόλουθος τύπος:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Απάντηση: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Παράδειγμα αρ. 5
Βρείτε $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.
Επειδή $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (θυμηθείτε ότι $\cos(0)=1$) και $\ lim_(x\to(0))x^2=0$, τότε έχουμε να κάνουμε με αβεβαιότητα της μορφής $\frac(0)(0)$. Ωστόσο, για να εφαρμόσετε το πρώτο αξιοσημείωτο όριο, θα πρέπει να απαλλαγείτε από το συνημίτονο στον αριθμητή, προχωρώντας στα ημίτονο (για να εφαρμόσετε στη συνέχεια τον τύπο) ή τις εφαπτομένες (για να εφαρμόσετε στη συνέχεια τον τύπο). Αυτό μπορεί να γίνει με τον ακόλουθο μετασχηματισμό:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$
Ας επιστρέψουμε στο όριο:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$
Το κλάσμα $\frac(\sin^2(5x))(x^2)$ είναι ήδη κοντά στη μορφή που απαιτείται για το πρώτο αξιοσημείωτο όριο. Ας δουλέψουμε λίγο με το κλάσμα $\frac(\sin^2(5x))(x^2)$, προσαρμόζοντάς το στο πρώτο αξιοσημείωτο όριο (σημειώστε ότι οι εκφράσεις στον αριθμητή και κάτω από το ημίτονο πρέπει να ταιριάζουν):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$
Ας επιστρέψουμε στο επίμαχο όριο:
$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0 ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Απάντηση: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Παράδειγμα αρ. 6
Βρείτε το όριο $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.
Αφού $\lim_(x\to(0))(1-\cos(6x))=0$ και $\lim_(x\to(0))(1-\cos(2x))=0$, τότε έχουμε να κάνουμε με αβεβαιότητα $\frac(0)(0)$. Ας το αποκαλύψουμε με τη βοήθεια του πρώτου αξιοσημείωτου ορίου. Για να γίνει αυτό, ας περάσουμε από συνημίτονα σε ημίτονο. Αφού $1-\cos(2\alpha)=2\sin^2(\alpha)$, τότε:
$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Περνώντας στα ημιτόνια στο δεδομένο όριο, θα έχουμε:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\αριστερά|\frac(0)(0)\δεξιά| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))(3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\αριστερά(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Απάντηση: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Παράδειγμα αρ. 7
Υπολογίστε το όριο $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ με την επιφύλαξη $\alpha\neq \ beta$.
Λεπτομερείς εξηγήσεις δόθηκαν νωρίτερα, αλλά εδώ απλά σημειώνουμε ότι και πάλι υπάρχει αβεβαιότητα $\frac(0)(0)$. Ας περάσουμε από συνημίτονα σε ημίτονο χρησιμοποιώντας τον τύπο
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Χρησιμοποιώντας αυτόν τον τύπο, παίρνουμε:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\δεξιά| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$
Απάντηση: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ άλφα^2)(2)$.
Παράδειγμα αρ. 8
Βρείτε το όριο $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.
Επειδή $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (θυμηθείτε ότι $\sin(0)=\tg(0)=0$) και $\ lim_(x\to(0))x^3=0$, τότε εδώ έχουμε να κάνουμε με αβεβαιότητα της μορφής $\frac(0)(0)$. Ας το αναλύσουμε ως εξής:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$
Απάντηση: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Παράδειγμα Νο. 9
Βρείτε το όριο $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.
Αφού $\lim_(x\to(3))(1-\cos(x-3))=0$ και $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, τότε υπάρχει αβεβαιότητα για τη μορφή $\frac(0)(0)$. Πριν προχωρήσετε στην επέκτασή της, είναι βολικό να κάνετε μια αλλαγή μεταβλητής με τέτοιο τρόπο ώστε η νέα μεταβλητή να τείνει στο μηδέν (σημειώστε ότι στους τύπους η μεταβλητή $\alpha \σε 0$). Ο ευκολότερος τρόπος είναι να εισαγάγετε τη μεταβλητή $t=x-3$. Ωστόσο, για λόγους ευκολίας περαιτέρω μετασχηματισμών (αυτό το όφελος μπορεί να φανεί στην πορεία της λύσης παρακάτω), αξίζει να κάνετε την ακόλουθη αντικατάσταση: $t=\frac(x-3)(2)$. Σημειώνω ότι και οι δύο αντικαταστάσεις ισχύουν σε αυτήν την περίπτωση, απλώς η δεύτερη αντικατάσταση θα σας επιτρέψει να εργάζεστε λιγότερο με κλάσματα. Από $x\to(3)$, τότε $t\to(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\αριστερά|\frac (0)(0)\δεξιά| =\αριστερά|\begin(ευθυγραμμισμένη)&t=\frac(x-3)(2);\\&t\to(0)\end(στοιχισμένη)\δεξιά| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ προς(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t)) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Απάντηση: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Παράδειγμα Νο. 10
Βρείτε το όριο $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2) $.
Για άλλη μια φορά έχουμε να κάνουμε με την αβεβαιότητα $\frac(0)(0)$. Πριν προχωρήσετε στην επέκτασή της, είναι βολικό να κάνετε μια αλλαγή μεταβλητής με τέτοιο τρόπο ώστε η νέα μεταβλητή να τείνει στο μηδέν (σημειώστε ότι στους τύπους η μεταβλητή είναι $\alpha\to(0)$). Ο ευκολότερος τρόπος είναι να εισαγάγετε τη μεταβλητή $t=\frac(\pi)(2)-x$. Αφού $x\to\frac(\pi)(2)$, τότε $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\αριστερά|\frac(0)(0)\δεξιά| =\αριστερά|\αρχή(ευθυγραμμισμένη)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(ευθυγραμμισμένη)\δεξιά| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0 ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Απάντηση: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.
Παράδειγμα Νο. 11
Βρείτε τα όρια $\lim_(x\to\frac(\pi)(2)\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2 \ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
Σε αυτή την περίπτωση δεν χρειάζεται να χρησιμοποιήσουμε το πρώτο υπέροχο όριο. Λάβετε υπόψη ότι τόσο το πρώτο όσο και το δεύτερο όριο περιέχουν μόνο τριγωνομετρικές συναρτήσεις και αριθμούς. Συχνά σε παραδείγματα αυτού του είδους είναι δυνατό να απλοποιηθεί η έκφραση που βρίσκεται κάτω από το σύμβολο ορίου. Επιπλέον, μετά την προαναφερθείσα απλοποίηση και μείωση κάποιων παραγόντων, η αβεβαιότητα εξαφανίζεται. Έδωσα αυτό το παράδειγμα για έναν μόνο σκοπό: να δείξω ότι η παρουσία τριγωνομετρικών συναρτήσεων κάτω από το πρόσημο ορίου δεν σημαίνει απαραίτητα τη χρήση του πρώτου αξιοσημείωτου ορίου.
Επειδή $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (θυμηθείτε ότι $\sin\frac(\pi)(2)=1$ ) και $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (να σας υπενθυμίσω ότι $\cos\frac(\pi)(2)=0$), τότε έχουμε που αντιμετωπίζει την αβεβαιότητα της μορφής $\frac(0)(0)$. Ωστόσο, αυτό δεν σημαίνει ότι θα χρειαστεί να χρησιμοποιήσουμε το πρώτο υπέροχο όριο. Για να αποκαλυφθεί η αβεβαιότητα, αρκεί να λάβουμε υπόψη ότι $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
Μια παρόμοια λύση υπάρχει στο βιβλίο λύσεων του Demidovich (αρ. 475). Όσον αφορά το δεύτερο όριο, όπως και στα προηγούμενα παραδείγματα αυτής της ενότητας, έχουμε μια αβεβαιότητα της μορφής $\frac(0)(0)$. Γιατί προκύπτει; Προκύπτει επειδή $\tg\frac(2\pi)(3)=-\sqrt(3)$ και $2\cos\frac(2\pi)(3)=-1$. Χρησιμοποιούμε αυτές τις τιμές για να μετατρέψουμε τις εκφράσεις στον αριθμητή και στον παρονομαστή. Στόχος των ενεργειών μας είναι να γράψουμε το άθροισμα στον αριθμητή και στον παρονομαστή ως γινόμενο. Παρεμπιπτόντως, συχνά σε έναν παρόμοιο τύπο είναι βολικό να αλλάζετε μια μεταβλητή, κατασκευασμένη με τέτοιο τρόπο ώστε η νέα μεταβλητή να τείνει στο μηδέν (δείτε, για παράδειγμα, παραδείγματα Νο. 9 ή Νο. 10 σε αυτήν τη σελίδα). Ωστόσο, σε αυτό το παράδειγμα δεν έχει νόημα η αντικατάσταση, αν και εάν είναι επιθυμητό, η αντικατάσταση της μεταβλητής $t=x-\frac(2\pi)(3)$ δεν είναι δύσκολη στην υλοποίηση.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2 \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$
Όπως καταλαβαίνετε, δεν χρειάστηκε να εφαρμόσουμε το πρώτο υπέροχο όριο. Φυσικά, μπορείτε να το κάνετε αυτό αν θέλετε (βλ. σημείωση παρακάτω), αλλά δεν είναι απαραίτητο.
Ποια είναι η λύση χρησιμοποιώντας το πρώτο αξιοσημείωτο όριο; εμφάνιση απόκρυψη
Χρησιμοποιώντας το πρώτο αξιοσημείωτο όριο παίρνουμε:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ δεξιά))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$
Απάντηση: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3)\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3)) $.
Το πρώτο αξιοσημείωτο όριο χρησιμοποιείται συχνά για τον υπολογισμό ορίων που περιέχουν ημίτονο, τόξο, εφαπτομένη, τόξο και τις προκύπτουσες αβεβαιότητες του μηδενός διαιρούμενο με το μηδέν.
Τύπος
Ο τύπος για το πρώτο αξιοσημείωτο όριο είναι: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$
Σημειώνουμε ότι για $ \alpha\to 0 $ παίρνουμε $ \sin\alpha \to 0 $, επομένως έχουμε μηδενικά στον αριθμητή και στον παρονομαστή. Έτσι, ο τύπος του πρώτου αξιοσημείωτου ορίου χρειάζεται για να αποκαλύψει τις αβεβαιότητες $ \frac(0)(0) $.
Για να εφαρμοστεί ο τύπος, πρέπει να πληρούνται δύο προϋποθέσεις:
- Οι εκφράσεις που περιέχονται στο ημίτονο και ο παρονομαστής του κλάσματος είναι ίδιες
- Οι εκφράσεις στο ημίτονο και στον παρονομαστή ενός κλάσματος τείνουν στο μηδέν
Προσοχή! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Αν και οι εκφράσεις κάτω από το ημίτονο και στον παρονομαστή είναι ίδιες, ωστόσο $ 2x ^2+1 = 1 $, για $ x\ έως 0 $. Η δεύτερη προϋπόθεση δεν πληρούται, οπότε ΔΕΝ ΜΠΟΡΕΙΣ να εφαρμόσεις τον τύπο!
Συνέπειες
Πολύ σπάνια στις εργασίες μπορείς να δεις ένα καθαρό πρώτο υπέροχο όριο, στο οποίο θα μπορούσες να γράψεις αμέσως την απάντηση. Στην πράξη, όλα φαίνονται λίγο πιο περίπλοκα, αλλά για τέτοιες περιπτώσεις θα είναι χρήσιμο να γνωρίζουμε τις συνέπειες του πρώτου αξιοσημείωτου ορίου. Χάρη σε αυτά, μπορείτε να υπολογίσετε γρήγορα τα απαιτούμενα όρια.
$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$
$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$
Παραδείγματα λύσεων
Ας εξετάσουμε το πρώτο αξιοσημείωτο όριο, παραδείγματα της λύσης του για τον υπολογισμό ορίων που περιέχουν τριγωνομετρικές συναρτήσεις και αβεβαιότητα $ \bigg[\frac(0)(0)\bigg] $
| Παράδειγμα 1 |
| Υπολογίστε $ \lim_(x\έως 0) \frac(\sin2x)(4x) $ |
| Λύση |
|
Ας δούμε το όριο και ας παρατηρήσουμε ότι περιέχει ένα ημίτονο. Στη συνέχεια, αντικαθιστούμε $ x = 0 $ στον αριθμητή και στον παρονομαστή και παίρνουμε την αβεβαιότητα μηδέν διαιρούμενη με το μηδέν: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)(0 ) $$ Ήδη δύο σημάδια ότι πρέπει να εφαρμόσουμε ένα υπέροχο όριο, αλλά υπάρχει μια μικρή απόχρωση: δεν μπορούμε να εφαρμόσουμε αμέσως τον τύπο, καθώς η έκφραση κάτω από το ημιτονικό πρόσημο διαφέρει από την έκφραση στον παρονομαστή. Και χρειαζόμαστε να είμαστε ίσοι. Επομένως, με τη βοήθεια στοιχειωδών μετασχηματισμών του αριθμητή θα τον μετατρέψουμε σε $2x$. Για να γίνει αυτό, θα βγάλουμε τα δύο από τον παρονομαστή του κλάσματος ως ξεχωριστό παράγοντα. Μοιάζει με αυτό: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ Παρακαλώ σημειώστε , ότι στο τέλος $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ ελήφθη σύμφωνα με τον τύπο. Εάν δεν μπορείτε να λύσετε το πρόβλημά σας, στείλτε το σε εμάς. Θα δώσουμε λεπτομερή λύση. Θα μπορείτε να δείτε την πρόοδο του υπολογισμού και να λάβετε πληροφορίες. Αυτό θα σας βοηθήσει να πάρετε τον βαθμό σας από τον δάσκαλό σας έγκαιρα! |
| Απάντηση |
| $$ \lim_(x\έως 0) \frac(\sin2x)(4x) =\frac(1)(2) $$ |
| Παράδειγμα 2 |
| Βρείτε $ \lim_(x\έως 0) \frac(\sin(x^3+2x))(2x-x^4) $ |
| Λύση |
|
Όπως πάντα, πρέπει πρώτα να μάθετε το είδος της αβεβαιότητας. Αν διαιρεθεί το μηδέν με το μηδέν, τότε δίνουμε προσοχή στην παρουσία ενός ημιτόνου: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ Αυτή η αβεβαιότητα μας επιτρέπει να χρησιμοποιήσουμε τον τύπο του πρώτου αξιοσημείωτου ορίου, αλλά η έκφραση από τον παρονομαστή δεν είναι ίση με το όρισμα του ημιτόνου; Ως εκ τούτου, ο τύπος δεν μπορεί να εφαρμοστεί "κατά μέτωπο". Είναι απαραίτητο να πολλαπλασιάσουμε και να διαιρέσουμε το κλάσμα με το όρισμα του ημιτόνου: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x -x^4)(x ^3+2x)) = $$ Τώρα γράφουμε τις ιδιότητες των ορίων: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x -x^4)\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ Το δεύτερο όριο ταιριάζει ακριβώς στον τύπο και είναι ίσο σε ένα: $$ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x )(2x-x^4) = $$ Αντικαταστήστε ξανά το $ x = 0 $ σε ένα κλάσμα και παίρνουμε την αβεβαιότητα $ \frac(0)(0) $. Για να το εξαλείψετε, αρκεί να αφαιρέσετε $ x $ από αγκύλες και να το μειώσετε κατά: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\έως 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2 )(2) = 1 $$ |
| Απάντηση |
| $$ \lim_(x\έως 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$ |
| Παράδειγμα 4 |
| Υπολογίστε $ \lim_(x\to0) \frac(\sin2x)(tg3x) $ |
| Λύση |
|
Ας ξεκινήσουμε τον υπολογισμό με την αντικατάσταση $ x=0 $. Ως αποτέλεσμα, λαμβάνουμε την αβεβαιότητα $ \frac(0)(0) $. Το όριο περιέχει ένα ημίτονο και μια εφαπτομένη, που υποδηλώνει μια πιθανή εξέλιξη της κατάστασης χρησιμοποιώντας τον τύπο του πρώτου αξιοσημείωτου ορίου. Ας μετατρέψουμε τον αριθμητή και τον παρονομαστή του κλάσματος σε τύπο και συνέπεια: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Τώρα βλέπουμε ότι στον αριθμητή και στον παρονομαστή υπάρχουν εκφράσεις που ταιριάζουν με τον τύπο και τις συνέπειες. Το όρισμα ημιτόνου και το όρισμα της εφαπτομένης είναι το ίδιο για τους αντίστοιχους παρονομαστές $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$ |
| Απάντηση |
| $$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$ |
Το άρθρο: "Το πρώτο αξιοσημείωτο όριο, παραδείγματα λύσεων" μίλησε για περιπτώσεις στις οποίες συνιστάται η χρήση αυτού του τύπου και των συνεπειών του.
Αυτό το άρθρο: «Το δεύτερο αξιοσημείωτο όριο» είναι αφιερωμένο στην αποκάλυψη εντός των ορίων αβεβαιοτήτων της μορφής:
$ \bigg[\frac(\infty)(\infty)\bigg]^\infty $ και $ ^\infty $.
Επίσης, τέτοιες αβεβαιότητες μπορούν να αποκαλυφθούν χρησιμοποιώντας τον λογάριθμο της εκθετικής συνάρτησης, αλλά αυτή είναι μια άλλη μέθοδος λύσης, η οποία θα καλυφθεί σε άλλο άρθρο.
Φόρμουλα και συνέπειες
Τύποςτο δεύτερο αξιοσημείωτο όριο γράφεται ως εξής: $$ \lim_(x \to \infty) \bigg (1+\frac(1)(x)\bigg)^x = e, \text( where ) e \περίπου 2,718 $$
Από τον τύπο προκύπτει συνέπειες, τα οποία είναι πολύ βολικά στη χρήση για την επίλυση παραδειγμάτων με όρια: $$ \lim_(x \to \infty) \bigg (1 + \frac(k)(x) \bigg)^x = e^k, \text( όπου ) k \in \mathbb(R) $$ $$ \lim_(x \to \infty) \bigg (1 + \frac(1)(f(x)) \bigg)^(f(x)) = e $ $ $$ \lim_(x \έως 0) \bigg (1 + x \bigg)^\frac(1)(x) = e $$
Αξίζει να σημειωθεί ότι το δεύτερο αξιοσημείωτο όριο δεν μπορεί να εφαρμοστεί πάντα σε μια εκθετική συνάρτηση, αλλά μόνο σε περιπτώσεις όπου η βάση τείνει προς την ενότητα. Για να το κάνετε αυτό, πρώτα υπολογίστε διανοητικά το όριο της βάσης και μετά βγάλτε συμπεράσματα. Όλα αυτά θα συζητηθούν σε παραδείγματα λύσεων.
Παραδείγματα λύσεων
Ας δούμε παραδείγματα λύσεων που χρησιμοποιούν τον άμεσο τύπο και τις συνέπειές του. Θα αναλύσουμε επίσης περιπτώσεις στις οποίες ο τύπος δεν χρειάζεται. Αρκεί να γράψετε μόνο μια έτοιμη απάντηση.
| Παράδειγμα 1 |
| Βρείτε το όριο $ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) $ |
| Λύση |
|
Ας αντικαταστήσουμε το άπειρο στο όριο και ας δούμε την αβεβαιότητα: $$ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) = \bigg (\frac (\infty)(\infty)\bigg)^\infty $$ Ας βρούμε το όριο της βάσης: $$ \lim_(x\to\infty) \frac(x+4)(x+3)= \lim_(x\to\infty) \frac(x(1+\frac (4)() x)))(x(1+\frac(3)(x))) = 1 $$ Έχουμε λάβει μια βάση ίση με ένα, που σημαίνει ότι μπορούμε ήδη να εφαρμόσουμε το δεύτερο αξιοσημείωτο όριο. Για να γίνει αυτό, ας προσαρμόσουμε τη βάση της συνάρτησης στον τύπο αφαιρώντας και προσθέτοντας ένα: $$ \lim_(x\to\infty) \bigg(1 + \frac(x+4)(x+3) - 1 \bigg)^(x+3) = \lim_(x\to\infty) \ big(1 + \frac(1)(x+3) \bigg)^(x+3) = $$ Ας δούμε το δεύτερο συμπέρασμα και ας γράψουμε την απάντηση: $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ Εάν δεν μπορείτε να λύσετε το πρόβλημά σας, στείλτε το σε εμάς. Θα δώσουμε λεπτομερή λύση. Θα μπορείτε να δείτε την πρόοδο του υπολογισμού και να λάβετε πληροφορίες. Αυτό θα σας βοηθήσει να πάρετε τον βαθμό σας από τον δάσκαλό σας έγκαιρα! |
| Απάντηση |
| $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ |
| Παράδειγμα 4 |
| Λύστε το όριο $ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) $ |
| Λύση |
|
Βρίσκουμε το όριο της βάσης και βλέπουμε ότι $ \lim_(x\to\infty) \frac(3x^2+4)(3x^2-2) = 1 $, που σημαίνει ότι μπορούμε να εφαρμόσουμε το δεύτερο αξιοσημείωτο όριο. Σύμφωνα με το πρότυπο σχέδιο, προσθέτουμε και αφαιρούμε ένα από τη βάση του βαθμού: $$ \lim_(x\to \infty) \bigg (1+\frac(3x^2+4)(3x^2-2)-1 \bigg) ^(3x) = \lim_(x\to \infty ) \bigg (1+\frac(6)(3x^2-2) \bigg) ^(3x) = $$ Προσαρμόζουμε το κλάσμα στον τύπο της 2ης νότας. όριο: $$ = \lim_(x\to \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(3x) = $$ Τώρα ας προσαρμόσουμε το βαθμό. Η ισχύς πρέπει να περιέχει ένα κλάσμα ίσο με τον παρονομαστή της βάσης $ \frac(3x^2-2)(6) $. Για να το κάνετε αυτό, πολλαπλασιάστε και διαιρέστε το βαθμό με αυτόν και συνεχίστε να λύνετε: $$ = \lim_(x\έως \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(\frac(3x^2-2) (6) \cdot \frac(6)(3x^2-2)\cdot 3x) = \lim_(x\to \infty) e^(\frac(18x)(3x^2-2)) = $$ Το όριο που βρίσκεται στην ισχύ στο $ e $ είναι ίσο με: $ \lim_(x\to \infty) \frac(18x)(3x^2-2) = 0 $. Επομένως, συνεχίζοντας τη λύση έχουμε: |
| Απάντηση |
| $$ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) = 1 $$ |
Ας εξετάσουμε περιπτώσεις όπου το πρόβλημα είναι παρόμοιο με το δεύτερο αξιοσημείωτο όριο, αλλά μπορεί να λυθεί χωρίς αυτό.
Στο άρθρο: «Το δεύτερο αξιοσημείωτο όριο: Παραδείγματα λύσεων» αναλύθηκε ο τύπος, οι συνέπειές του και δόθηκαν συνήθεις τύποι προβλημάτων σε αυτό το θέμα.
