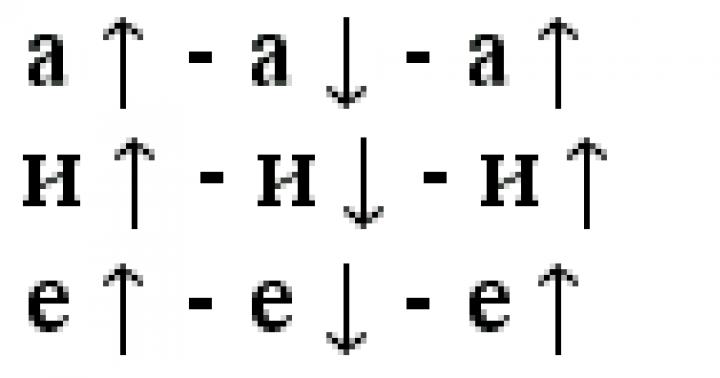Rețineți că în cele ce urmează, fără pierderi de generalitate, vom lua în considerare cazul vectorilor din spațiul tridimensional. Pe plan, luarea în considerare a vectorilor se realizează într-un mod similar. După cum sa menționat mai sus, toate rezultatele cunoscute din cursul algebrei liniare pentru vectori algebrici pot fi transferate în cazul special al vectorilor geometrici. Deci hai sa o facem.
Lasă vectorii să fie fixați.
Definiție. Suma, unde sunt unele numere, se numește o combinație liniară de vectori. În acest caz, aceste numere vor fi numite coeficienții combinației liniare.
Ne va interesa problema posibilității de egalitate a unei combinații liniare cu un vector zero. În conformitate cu proprietățile și axiomele spațiilor vectoriale, devine evident că pentru orice sistem de vectori există o mulțime trivială (zero) de coeficienți pentru care această egalitate este valabilă:
Se pune problema existenței pentru un sistem dat de vectori a unei mulțimi netriviale de coeficienți (printre care există cel puțin un coeficient nenul), pentru care egalitatea menționată este valabilă. În conformitate cu aceasta, vom distinge între sisteme liniar dependente și independente.
Definiție. Un sistem de vectori se numește liniar independent dacă există o astfel de mulțime de numere, printre care există cel puțin unul diferit de zero, astfel încât combinația liniară corespunzătoare să fie egală cu vectorul zero:
Un sistem de vectori se numește liniar independent dacă egalitatea
este posibilă numai în cazul unui set trivial de coeficienți:
Să enumerăm principalele proprietăți ale sistemelor liniar dependente și independente demonstrate în cursul algebrei liniare.
1. Orice sistem de vectori care conține un vector zero este dependent liniar.
2. Să existe un subsistem dependent liniar în sistemul de vectori. Atunci întregul sistem este, de asemenea, dependent liniar.
3. Dacă un sistem de vectori este liniar independent, atunci oricare dintre subsistemele sale este, de asemenea, liniar independent.
4. Dacă într-un sistem de vectori există doi vectori, dintre care unul se obține din celălalt prin înmulțirea cu un anumit număr, atunci întregul sistem este dependent liniar.
Teorema (criteriul dependenței liniare). Un sistem de vectori este dependent liniar dacă și numai dacă unul dintre vectorii acestui sistem poate fi reprezentat ca o combinație liniară a celorlalți vectori ai sistemului.
Ținând cont de criteriul coliniarității a doi vectori, se poate susține că criteriul dependenței liniare a acestora este coliniaritatea lor. Pentru trei vectori din spațiu, următoarea afirmație este adevărată.
Teoremă (criteriul dependenței liniare a trei vectori geometrici). Trei vectori și sunt dependenți liniar dacă și numai dacă sunt coplanari.
Dovada.
Nevoie. Fie vectorii și să fie liniar dependenți. Haideți să le dovedim comparabilitatea. Apoi, conform criteriului general al dependenței liniare a vectorilor algebrici, afirmăm că unul dintre acești vectori poate fi reprezentat ca o combinație liniară a altor vectori. Să, de exemplu,
Dacă toți cei trei vectori și sunt aplicați la o origine comună, atunci vectorul va coincide cu diagonala paralelogramului construit pe vectorii și. Dar aceasta înseamnă că vectorii și se află în același plan, adică. coplanare.
Adecvarea. Fie vectorii și să fie coplanari. Să arătăm că sunt dependente liniar. În primul rând, luați în considerare cazul în care orice pereche de vectori indicați este coliniară. În acest caz, conform teoremei anterioare, sistemul de vectori , , conține un subsistem dependent liniar și, prin urmare, este el însuși dependent liniar conform proprietății 2 a sistemelor de vectori liniar dependente și independente. Să nu fie acum coliniar nicio pereche de vectori luati în considerare. Transferăm toți cei trei vectori într-un singur plan și îi aducem la o origine comună. Desenați până la capătul liniilor vectoriale paralele cu vectorii și . Fie ca litera să desemneze punctul de intersecție al dreptei paralele cu vectorul cu linia pe care se află vectorul și prin literă punctul de intersecție al dreptei paralele cu vectorul cu dreapta pe care se află vectorul. Prin definiția sumei vectorilor, obținem:
![]() .
.
Deoarece vectorul este coliniar cu un vector diferit de zero, există un număr real astfel încât
Consideraţii similare implică existenţa unui număr real astfel încât
Ca urmare, vom avea:
Apoi, din criteriul general pentru dependența liniară a vectorilor algebrici, obținem că vectorii , , sunt liniar dependenți. ■
Teorema (dependența liniară a patru vectori). Oricare patru vectori sunt dependenți liniar.
Dovada. În primul rând, luați în considerare cazul în care orice triplu dintre cei patru vectori indicați este coplanar. În acest caz, acest triplu este dependent liniar în conformitate cu teorema anterioară. Prin urmare, în conformitate cu proprietatea a 2 sisteme de vectori dependente liniar și independente, și întregul cvadruplu este dependent liniar.
Să fie acum, printre vectorii luați în considerare, niciun triplu de vectori să nu fie coplanar. Să aducem toți cei patru vectori , , , la un început comun și să desenăm plane până la sfârșitul vectorului paralel cu planurile definite de perechi de vectori , ; , ; , . Punctele de intersecție ale planurilor indicate cu liniile pe care se află vectorii și sunt notate cu literele și, respectiv. Din definiţia sumei vectorilor rezultă că
care, ținând cont de criteriul general al dependenței liniare a vectorilor algebrici, spune că toți cei patru vectori sunt liniar dependenți. ■
Fie funcțiile , au derivate ale limitei (n-1).
Luați în considerare determinantul:  (1)
(1)
W(x) se numește determinant Wronsky pentru funcții.
Teorema 1. Dacă funcțiile sunt dependente liniar în intervalul (a, b), atunci Wronskianul lor W(x) este identic egal cu zero în acest interval.
Dovada. După condiția teoremei, relația
, (2) unde nu toate sunt egale cu zero. Lăsa . Apoi
![]() (3). Diferențiază această identitate de n-1 ori și,
(3). Diferențiază această identitate de n-1 ori și,
Înlocuind în loc de valorile lor obținute în determinantul Vronsky,
primim:
 (4).
(4).
În determinantul Wronsky, ultima coloană este o combinație liniară a coloanelor anterioare n-1 și, prin urmare, este zero în toate punctele din intervalul (a, b).
Teorema 2. Dacă funcțiile y1,…, yn sunt soluții liniar independente ale ecuației L[y] = 0, a căror toți coeficienții sunt continui în intervalul (a, b), atunci Wronskianul acestor soluții este diferit de zero în fiecare punct al intervalul (a, b).
Dovada. Să presupunem contrariul. Există X0, unde W(X0)=0. Compunem un sistem de n ecuații
 (5).
(5).
În mod evident, sistemul (5) are o soluție diferită de zero. Fie (6).
Să compunem o combinație liniară de soluții y1,…, yn.
Y(x) este o soluție a ecuației L[y] = 0. În plus, . În virtutea teoremei unicității, soluția ecuației L[y] = 0 cu condiții inițiale zero nu poate fi decât zero, adică .
Obținem identitatea , unde nu toate sunt egale cu zero, ceea ce înseamnă că y1,…, yn sunt dependente liniar, ceea ce contrazice condiția teoremei. Prin urmare, nu există un astfel de punct în care W(X0)=0.
Pe baza teoremei 1 și teoremei 2, putem formula următoarea afirmație. Pentru ca n soluții ale ecuației L[y] = 0 să fie liniar independente în intervalul (a, b), este necesar și suficient ca Wronskianul lor să nu dispară în niciun punct al acestui interval.
Din teoremele demonstrate rezultă următoarele proprietăți evidente ale lui Wronskian.
- Dacă Wronskianul a n soluții ale ecuației L[y] = 0 este egal cu zero într-un punct x = x0 din intervalul (a, b) în care toți coeficienții pi(x) sunt continui, atunci este egal cu zero în toate punctele acestui interval.
- Dacă Wronskianul a n soluții ale ecuației L[y] = 0 este diferit de zero într-un punct x = x0 din intervalul (a, b), atunci este diferit de zero în toate punctele acestui interval.
Astfel, pentru liniaritatea a n soluții independente ale ecuației L[y] = 0 în intervalul (a, b), în care coeficienții ecuației pi(x) sunt continui, este necesar și suficient ca Wronskianul lor să fie diferit de zero cel puțin într-un punct al acestui interval.
Introdus de noi operații liniare pe vectori fac posibilă crearea diferitelor expresii pentru cantități vectorialeși transformați-le folosind proprietățile setate pentru aceste operații.
Pe baza unui set dat de vectori a 1 , ... și n , puteți compune o expresie de forma
unde a 1 , ... și n sunt numere reale arbitrare. Această expresie se numește combinație liniară de vectori a 1 , ..., a n . Numerele α i , i = 1, n , sunt coeficienți de combinație liniară. Se mai numește și mulțimea vectorilor sistem vectorial.
În legătură cu conceptul introdus de combinație liniară de vectori, se pune problema descrierii mulțimii de vectori care pot fi scrise ca o combinație liniară a unui sistem dat de vectori a 1 , ..., a n . În plus, întrebările despre condițiile în care există o reprezentare a unui vector sub forma unei combinații liniare și despre unicitatea unei astfel de reprezentări sunt naturale.
Definiție 2.1. Vectorii a 1 , ... și n sunt numiți dependent liniar, dacă există o astfel de mulțime de coeficienți α 1 , ... , α n , că
α 1 a 1 + ... + α n a n = 0 (2.2)
și cel puțin unul dintre acești coeficienți este diferit de zero. Dacă setul specificat de coeficienți nu există, atunci vectorii sunt numiți liniar independent.
Dacă α 1 = ... = α n = 0, atunci, evident, α 1 a 1 + ... + α n a n = 0. Având în vedere acest lucru, putem spune următoarele: vectori a 1 , ..., și n sunt liniar independenți dacă din egalitatea (2.2) rezultă că toți coeficienții α 1 , ... , α n sunt egali cu zero.
Următoarea teoremă explică de ce noul concept este numit termenul „dependență” (sau „independență”) și oferă un criteriu simplu pentru dependența liniară.
Teorema 2.1. Pentru ca vectorii a 1 , ..., și n , n > 1, să fie liniar dependenți, este necesar și suficient ca unul dintre ei să fie o combinație liniară a celorlalți.
◄ Necesitatea. Să presupunem că vectorii a 1 , ... și n sunt dependenți liniar. Conform definiției 2.1 a dependenței liniare, în egalitatea (2.2) există cel puțin un coeficient diferit de zero în stânga, de exemplu α 1 . Lăsând primul termen în partea stângă a egalității, mutăm restul în partea dreaptă, schimbându-le semnele ca de obicei. Împărțind egalitatea rezultată la α 1 , obținem
a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n / α 1 ⋅ a n
acestea. reprezentarea vectorului a 1 ca o combinație liniară a vectorilor rămași a 2 , ... și n .
Adecvarea. Fie, de exemplu, primul vector a 1 poate fi reprezentat ca o combinație liniară a vectorilor rămași: a 1 = β 2 a 2 + ... + β n a n . Transferând toți termenii din partea dreaptă spre stânga, obținem un 1 - β 2 a 2 - ... - β n a n = 0, adică. combinație liniară de vectori a 1 , ... și n cu coeficienți α 1 = 1, α 2 = - β 2 , ..., α n = - β n , egal cu vector zero.În această combinație liniară, nu toți coeficienții sunt egali cu zero. Conform definiției 2.1, vectorii a 1 , ... și n sunt dependenți liniar.
Definiția și criteriul dependenței liniare sunt formulate în așa fel încât să implice prezența a doi sau mai mulți vectori. Totuși, se poate vorbi și despre o dependență liniară a unui vector. Pentru a realiza această posibilitate, în loc de „vectorii sunt dependenți liniar” trebuie să spunem „sistemul de vectori este dependent liniar”. Este ușor de observat că expresia „un sistem de un vector este dependent liniar” înseamnă că acest singur vector este zero (există un singur coeficient într-o combinație liniară și nu trebuie să fie egal cu zero).
Conceptul de dependență liniară are o interpretare geometrică simplă. Această interpretare este clarificată de următoarele trei afirmații.
Teorema 2.2. Doi vectori sunt dependenți liniar dacă și numai dacă coliniare.
◄ Dacă vectorii a și b sunt dependenți liniar, atunci unul dintre ei, de exemplu a, este exprimat prin celălalt, adică. a = λb pentru un număr real λ. Conform definiției 1.7 lucrări vectori printr-un număr, vectorii a și b sunt coliniari.
Acum să fie vectorii a și b coliniari. Dacă ambele sunt zero, atunci este evident că sunt dependente liniar, deoarece orice combinație liniară a acestora este egală cu vectorul zero. Fie ca unul dintre acești vectori să nu fie egal cu 0, de exemplu vectorul b. Notăm cu λ raportul lungimilor vectorilor: λ = |а|/|b|. Vectorii coliniari pot fi unidirecțional sau directii opuse. În acest din urmă caz, schimbăm semnul lui λ. Apoi, verificând Definiția 1.7, vedem că a = λb. Conform teoremei 2.1, vectorii a și b sunt liniar dependenți.
Observație 2.1.În cazul a doi vectori, ținând cont de criteriul dependenței liniare, teorema demonstrată poate fi reformulată astfel: doi vectori sunt coliniari dacă și numai dacă unul dintre ei este reprezentat ca produs al celuilalt printr-un număr. Acesta este un criteriu convenabil pentru coliniaritatea a doi vectori.
Teorema 2.3. Trei vectori sunt dependenți liniar dacă și numai dacă aceștia coplanare.
◄ Dacă trei vectori a, b, c sunt dependenți liniar, atunci, conform teoremei 2.1, unul dintre ei, de exemplu a, este o combinație liniară a celorlalți: a = βb + γc. Să combinăm originile vectorilor b și c în punctul A. Atunci vectorii βb, γc vor avea o origine comună în punctul A și paralelogramul își reglează suma, acestea. vector a, va fi un vector cu începutul A și Sfârşit, care este vârful unui paralelogram construit pe vectori sumanzi. Astfel, toți vectorii se află în același plan, adică sunt coplanari.
Fie vectorii a, b, c coplanari. Dacă unul dintre acești vectori este zero, atunci este evident că va fi o combinație liniară a celorlalți. Este suficient să luăm toți coeficienții combinației liniare egale cu zero. Prin urmare, putem presupune că toți cei trei vectori nu sunt zero. Compatibil start aceşti vectori într-un punct comun O. Fie capetele lor, respectiv, punctele A, B, C (Fig. 2.1). Desenați drepte prin punctul C paralele cu drepte care trec prin perechi de puncte O, A și O, B. Notând punctele de intersecție A" și B", obținem un paralelogram OA"CB", prin urmare, OC" = OA" + OB " . Vector OA" și vectorul diferit de zero a= OA sunt coliniari și, prin urmare, primul dintre ele poate fi obținut prin înmulțirea celui de-al doilea cu un număr real α:OA" = αOA. În mod similar, OB" = βOB , β ∈ R. Ca rezultat, obținem că OC" = α OA + βOB , adică vectorul c este o combinație liniară a vectorilor a și b. Conform teoremei 2.1, vectorii a, b, c sunt liniar dependenți.

Teorema 2.4. Oricare patru vectori sunt dependenți liniar.
◄ Demonstrarea urmează aceeași schemă ca în teorema 2.3. Luați în considerare patru vectori arbitrari a, b, c și d. Dacă unul dintre cei patru vectori este zero, sau există doi vectori coliniari printre ei sau trei dintre cei patru vectori sunt coplanari, atunci acești patru vectori sunt dependenți liniar. De exemplu, dacă vectorii a și b sunt coliniari, atunci putem compune combinația lor liniară αa + βb = 0 cu coeficienți nenuli, apoi adăugați cei doi vectori rămași la această combinație, luând zerouri ca coeficienți. Obținem o combinație liniară de patru vectori egali cu 0, în care există coeficienți nenuli.
Astfel, putem presupune că dintre cei patru vectori aleși nu există nuli, nici doi nu sunt coliniari și nici trei nu sunt coplanari. Ca început comun alegem punctul O. Atunci capetele vectorilor a, b, c, d vor fi niște puncte A, B, C, D (Fig. 2.2). Prin punctul D trasăm trei plane paralele cu planurile ОВС, OCA, OAB, și fie A", B", С" punctele de intersecție ale acestor plane cu dreptele OA, OB, respectiv OS. Obținem un paralelipiped OA"C"B"C" B"DA", iar vectorii a, b, c se află pe marginile sale care ies din vârful O. Deoarece patrulaterul OC"DC" este un paralelogram, atunci OD = OC" + OC ". La rândul său, segmentul OS" este un paralelogram diagonal OA"C"B", deci OC" = OA" + OB" și OD = OA" + OB" + OC" .

Rămâne de observat că perechile de vectori OA ≠ 0 și OA" , OB ≠ 0 și OB" , OC ≠ 0 și OC" sunt coliniari și, prin urmare, putem alege coeficienții α, β, γ astfel încât OA" = αOA, OB" = βOB și OC" = yOC. În cele din urmă, obținem OD = αOA + βOB + γOC . În consecință, vectorul OD este exprimat în termenii celor trei vectori rămași, iar toți cei patru vectori, conform teoremei 2.1, sunt liniar dependenți.
Următoarele oferă câteva criterii pentru dependența liniară și, în consecință, independența liniară a sistemelor de vectori.
Teorema. (O condiție necesară și suficientă pentru dependența liniară a vectorilor.)
Un sistem de vectori este dependent dacă și numai dacă unul dintre vectorii sistemului este exprimat liniar în termenii celorlalți ai acestui sistem.
Dovada. Nevoie. Fie ca sistemul să fie dependent liniar. Apoi, prin definiție, reprezintă vectorul nul într-un mod netrivial, i.e. există o combinație non-trivială a acestui sistem de vectori egală cu vectorul zero:
unde cel puțin unul dintre coeficienții acestei combinații liniare nu este egal cu zero. Lăsa , .
Împărțiți ambele părți ale egalității anterioare la acest coeficient diferit de zero (adică înmulțiți cu:
Notați: , unde .
acestea. unul dintre vectorii sistemului este exprimat liniar în termenii celorlalți ai acestui sistem etc.
Adecvarea. Fie ca unul dintre vectorii sistemului să fie exprimat liniar în termenii altor vectori ai acestui sistem:
Să mutăm vectorul la dreapta acestei egalități:
Deoarece coeficientul vectorului este , atunci avem o reprezentare netrivială a zero de către sistemul de vectori , ceea ce înseamnă că acest sistem de vectori este dependent liniar etc.
Teorema a fost demonstrată.
Consecinţă.
1. Un sistem de vectori dintr-un spațiu vectorial este liniar independent dacă și numai dacă niciunul dintre vectorii sistemului nu este exprimat liniar în termenii altor vectori ai acestui sistem.
2. Un sistem de vectori care conțin un vector zero sau doi vectori egali este dependent liniar.
Dovada.
1) Necesitatea. Fie sistemul liniar independent. Presupunem contrariul și există un vector sistem care este exprimat liniar în termenii altor vectori ai acestui sistem. Apoi, după teoremă, sistemul este dependent liniar și ajungem la o contradicție.
Adecvarea. Niciunul dintre vectorii sistemului nu fie exprimat în termenii altora. Să presupunem contrariul. Fie ca sistemul să fie dependent liniar, dar din teoremă rezultă că există un vector sistem care este exprimat liniar prin alți vectori ai acestui sistem și ajungem din nou la o contradicție.
2a) Fie ca sistemul să conțină un vector zero. Presupunem pentru certitudine că vectorul :. Apoi egalitatea
acestea. unul dintre vectorii sistemului este exprimat liniar în termenii celorlalți vectori ai acestui sistem. Din teoremă rezultă că un astfel de sistem de vectori este dependent liniar, așa mai departe.
Rețineți că acest fapt poate fi demonstrat direct dintr-un sistem de vectori dependent liniar.
Deoarece , următoarea egalitate este evidentă
Aceasta este o reprezentare non-trivială a vectorului zero, ceea ce înseamnă că sistemul este dependent liniar.
2b) Fie ca sistemul să aibă doi vectori egali. Lasă pentru . Apoi egalitatea
Acestea. primul vector este exprimat liniar în termenii celorlalți vectori ai aceluiași sistem. Din teoremă rezultă că sistemul dat este dependent liniar și așa mai departe.
Similar cu cea precedentă, această aserțiune poate fi demonstrată și direct din definiția unui sistem dependent liniar.
O condiție necesară și suficientă pentru dependența liniară a doi
vectorii este coliniaritatea lor.
2. Produs scalar- o operație pe doi vectori, al cărei rezultat este un scalar (număr) care nu depinde de sistemul de coordonate și caracterizează lungimile vectorilor multiplicatori și unghiul dintre ei. Această operație corespunde înmulțirii lungime dat vector x pe proiecție un alt vector y la vectorul dat x. Această operație este de obicei privită ca comutativă și liniară în fiecare factor.
Proprietățile produsului punct:
3. Se numesc trei vectori (sau mai multi). coplanare dacă ei, reducându-se la o origine comună, se află în același plan.
O condiție necesară și suficientă pentru dependența liniară a trei vectori este coplanaritatea lor.Orice patru vectori sunt dependenți liniar. bază în spațiu se numește orice triplu ordonat al vectorilor necoplanari. O bază în spațiu permite să se asocieze în mod unic cu fiecare vector un triplu ordonat de numere - coeficienții reprezentării acestui vector într-o combinație liniară de vectori ai bazei. Dimpotrivă, cu ajutorul unei baze vom asocia câte un vector cu fiecare triplet ordonat de numere dacă facem o combinație liniară.O bază ortogonală se numește ortonormal , dacă vectorii săi sunt egali cu o lungime. Pentru o bază ortonormală în spațiu, notația este adesea folosită. Teorema: Pe o bază ortonormală, coordonatele vectorilor sunt proiecțiile ortogonale corespunzătoare ale acestui vector pe direcțiile vectorilor de coordonate. Un triplu de vectori necoplanari a, b, c numit dreapta, dacă observatorul de la originea lor comună ocolește capetele vectorilor a, b, cîn această ordine, se pare că merge în sensul acelor de ceasornic. In caz contrar a, b, c - a lăsat triplu. Se numesc toate triplele din dreapta (sau stânga) ale vectorilor orientat în mod egal. Un sistem de coordonate dreptunghiular pe un plan este format din două axe de coordonate reciproc perpendiculare BOUși OY. Axele de coordonate se intersectează într-un punct O, care se numește origine, fiecare axă are o direcție pozitivă. LA mana dreapta sistem de coordonate, direcția pozitivă a axelor este aleasă astfel încât cu direcția axei OY sus, axa BOU privi spre dreapta.
Patru unghiuri (I, II, III, IV) formate din axele de coordonate X"Xși Y"Y, se numesc unghiuri de coordonate sau cadranele(vezi fig. 1).
dacă vectorii și în raport cu o bază ortonormală pe plan au coordonate și, respectiv, atunci produsul scalar al acestor vectori se calculează prin formula
4. Produsul vectorial al doi vectori a și b este o operație asupra lor, definită doar în spațiul tridimensional, al cărei rezultat este vector cu urmatoarele
proprietati:
Sensul geometric al produsului încrucișat al vectorilor este aria unui paralelogram construit pe vectori. O condiție necesară și suficientă pentru coliniaritatea unui vector diferit de zero și a unui vector este existența unui număr care satisface egalitatea .
Dacă doi vectori și sunt definiți prin coordonatele lor carteziene dreptunghiulare, sau mai precis, ei sunt reprezentați într-o bază vortonormalizată
iar sistemul de coordonate este corect, atunci produsul lor vectorial are forma
Pentru a reține această formulă, este convenabil să folosiți determinantul:
5. Produs mixt vectori - produsul scalar al unui vector și produsul încrucișat al vectorilor și:
Uneori se numește produs scalar triplu vectori, aparent datorită faptului că rezultatul este un scalar (mai precis, un pseudoscalar).
Sensul geometric: Modulul produsului mixt este numeric egal cu volumul paralelipipedului format de vectori .
Când doi factori sunt interschimbați, produsul mixt își schimbă semnul invers:
Cu o permutare ciclică (circulară) a factorilor, produsul mixt nu se modifică:
Produsul amestecat este liniar în orice factor.
Produsul mixt este zero dacă și numai dacă vectorii sunt coplanari.
1. Condiție de complementaritate pentru vectori: trei vectori sunt coplanari dacă și numai dacă produsul lor mixt este zero.
§ Un triplu de vectori care conțin o pereche de vectori coliniari este coplanar.
§ Produsul mixt al vectorilor coplanari. Acesta este un criteriu pentru coplanaritatea a trei vectori.
§ Vectorii coplanari sunt dependenti liniar. Acesta este, de asemenea, un criteriu de coplanaritate.
§ Există numere reale astfel încât pentru coplanare , cu excepţia sau . Aceasta este o reformulare a proprietății anterioare și este, de asemenea, un criteriu de coplanaritate.
§ Într-un spațiu tridimensional formează o bază 3 vectori necoplanari. Adică, orice vector poate fi reprezentat ca: . Apoi vor fi coordonatele din baza dată.
Produsul mixt în sistemul de coordonate carteziene drept (în baza ortonormală) este egal cu determinantul matricei compuse din vectori și:
§6. Ecuația generală (completă) a planului
unde și sunt constante, în plus, și nu sunt egale cu zero în același timp; sub forma vectoriala:
unde este vectorul raza punctului , vectorul este perpendicular pe plan (vector normal). Cosinusuri de direcție vector:
Dacă unul dintre coeficienții din ecuația plană este zero, ecuația se numește incomplet. Când planul trece prin originea coordonatelor, când (sau , ) P. este paralelă cu axa (respectiv sau ). Pentru ( , sau ), planul este paralel cu planul (sau , respectiv).
§ Ecuația unui plan în segmente:
unde , , sunt segmentele tăiate de plan pe axe și .
§ Ecuația unui plan care trece printr-un punct perpendicular pe vectorul normal :
sub forma vectoriala:
(produs mixt al vectorilor), în caz contrar
§ Ecuație plană normală (normalizată).
§ Unghiul dintre două plane. Dacă ecuațiile P. sunt date sub forma (1), atunci
Dacă este în formă vectorială, atunci
§ Planurile sunt paralele, dacă
Sau (produs vectorial)
§ Planurile sunt perpendiculare, dacă
Sau . (produs scalar)
7. Ecuația unui plan care trece prin trei puncte date , neîntins pe aceeași linie:
8. Distanţa de la un punct la un plan este cea mai mică dintre distanţele dintre acest punct şi punctele planului. Se știe că distanța de la un punct la un plan este egală cu lungimea perpendicularei coborâte din acest punct în plan.
§ Abaterea punctului din planul dat de ecuația normalizată
Dacă și originea se află pe părți opuse ale planului, în caz contrar. Distanța de la un punct la un plan este
§ Distanța de la punct la planul dat de ecuație se calculează prin formula:
9. pachet de avion- ecuaţia oricărui P. care trece prin dreapta de intersecţie a două plane
unde α și β sunt numere care nu sunt egale simultan cu zero.
Pentru ca cele trei plane definite prin ecuațiile lor generale A 1 x+B 1 y+C 1 z+D 1 =0, A 2 x+B 2 y+C 2 z+D 2 =0, A 3 x+B 3 y+C 3 z+D 3 =0 în raport cu PDSC aparțineau unui fascicul, propriu sau impropriu, este necesar și suficient ca rangul matricei să fie egal fie cu doi, fie cu unul.
Teorema 2. Fie două plane π 1 și π 2 date în raport cu PDSC prin ecuațiile lor generale: A 1 x+B 1 y+C 1 z+D 1 =0, A 2 x+B 2 y+C 2 z +D2 = 0. Pentru ca planul π 3, dat relativ la PDSC prin ecuația sa generală A 3 x+B 3 y+C 3 z+D 3 =0, să aparțină fasciculului format din planele π 1 și π 2, este necesar și suficient ca partea stângă a ecuației planului π 3 să fie reprezentată ca o combinație liniară a părților din stânga ecuațiilor planelor π 1 și π 2 .
10.Ecuația parametrică vectorială a unei linii drepte in spatiu:
unde este vectorul rază a unui punct fix M 0 situat pe o linie dreaptă este un vector diferit de zero coliniar cu această linie dreaptă, este vectorul rază a unui punct arbitrar pe linie dreaptă.
Ecuația parametrică a unei drepte in spatiu:
M
Ecuația canonică a unei linii drepte in spatiu:
unde sunt coordonatele unui punct fix M 0 culcat pe linie dreaptă; - coordonatele unui vector coliniar acestei linii.
Ecuația vectorială generală a unei linii drepte in spatiu:
Deoarece linia este intersecția a două plane diferite neparalele, date, respectiv, de ecuațiile generale:
atunci ecuația unei linii drepte poate fi dată printr-un sistem de ecuații:
Unghiul dintre vectorii de direcție și va fi egal cu unghiul dintre linii. Unghiul dintre vectori este găsit folosind produsul scalar. cosA=(ab)/IaI*IbI
Unghiul dintre o linie dreaptă și un plan se găsește prin formula:
unde (A; B; C;) sunt coordonatele vectorului normal al planului
(l;m;n;) coordonatele vectorului de direcție ale dreptei
Condiții pentru paralelismul a două linii:
a) Dacă dreptele sunt date de ecuațiile (4) cu o pantă, atunci condiția necesară și suficientă pentru paralelismul lor este egalitatea pantelor lor:
k 1 = k 2 . (8)
b) Pentru cazul în care dreptele sunt date prin ecuații în forma generală (6), condiția necesară și suficientă pentru paralelismul lor este ca coeficienții la coordonatele curente corespunzătoare din ecuațiile lor să fie proporționali, i.e.
Condiții pentru perpendicularitatea a două drepte:
a) În cazul în care dreptele sunt date de ecuațiile (4) cu o pantă, condiția necesară și suficientă pentru perpendicularitatea lor este ca pantele lor să fie reciproce ca mărime și opuse ca semn, i.e.
b) Dacă ecuațiile dreptelor sunt date în forma generală (6), atunci condiția pentru perpendicularitatea lor (necesară și suficientă) este îndeplinirea egalității
A 1 A 2 + B 1 B 2 = 0. (12)
Se spune că o dreaptă este perpendiculară pe un plan dacă este perpendiculară pe orice dreaptă din acel plan. Dacă o dreaptă este perpendiculară pe fiecare dintre cele două drepte care se intersectează ale unui plan, atunci este perpendiculară pe acel plan. Pentru ca o dreaptă și un plan să fie paralele, este necesar și suficient ca vectorul normal pe plan și vectorul de direcție al dreptei să fie perpendiculare. Pentru aceasta, este necesar ca produsul lor scalar să fie egal cu zero.
Pentru ca o dreaptă și un plan să fie perpendiculare, este necesar și suficient ca vectorul normal pe plan și vectorul de direcție al dreptei să fie coliniare. Această condiție este îndeplinită dacă produsul încrucișat al acestor vectori a fost egal cu zero.
12. În spațiu, distanța de la un punct la o dreaptă dată de o ecuație parametrică
poate fi găsită ca distanța minimă de la un punct dat la un punct arbitrar pe o linie dreaptă. Coeficient t acest punct poate fi găsit prin formula
Distanța dintre liniile care se intersectează este lungimea perpendicularei lor comune. Este egală cu distanța dintre planele paralele care trec prin aceste drepte.