Mișcarea circulară uniformă este caracterizată prin mișcarea unui corp de-a lungul unui cerc. În acest caz, se schimbă doar direcția vitezei, iar mărimea acesteia rămâne constantă.
În general, un corp se mișcă pe o cale curbă și este dificil de descris. Pentru a simplifica descrierea mișcării curbilinie, aceasta este împărțită în tipuri mai simple de mișcare. În special, unul dintre aceste tipuri este mișcarea uniformă într-un cerc. Orice traiectorie curbă de mișcare poate fi împărțită în secțiuni de dimensiuni suficient de mici, în care corpul se va mișca aproximativ de-a lungul unui arc care face parte dintr-un cerc.
Când un corp se mișcă într-un cerc, viteza liniară este direcționată tangențial. În consecință, chiar dacă un corp se mișcă de-a lungul unui arc cu o viteză absolută constantă, direcția de mișcare în fiecare punct va fi diferită. Astfel, orice mișcare într-un cerc este o mișcare cu accelerație.
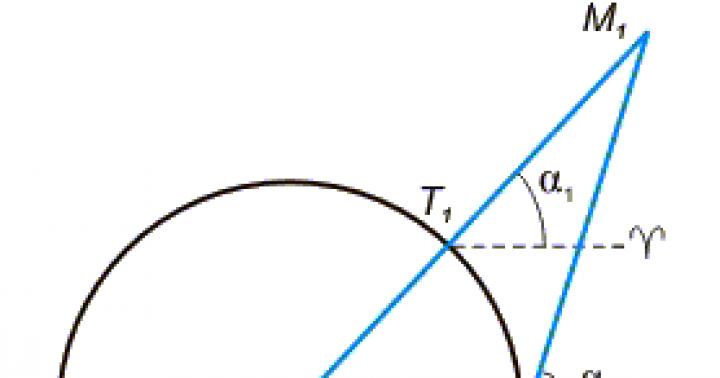
Imaginează-ți un cerc de-a lungul căruia se mișcă un punct material. În momentul zero de timp, se află în poziţia A. După un anumit interval de timp, ajunge în punctul B. Dacă trasăm doi vectori cu rază de la centrul cercului până la punctul A şi punctul B, atunci un anumit unghi va se obtine intre ei. Să-i spunem unghiul phi. Dacă, în perioade egale de timp, un punct se rotește prin același unghi phi, atunci o astfel de mișcare se numește uniformă, iar viteza se numește unghiulară.
Figura 1 - viteza unghiulara.
Viteza unghiulară se măsoară în rotații pe secundă. O revoluție pe secundă este atunci când un punct trece de-a lungul întregului cerc și revine la poziția inițială, luând o secundă. Această cifră de afaceri se numește perioada de circulație. Reciproca perioadei de rotație se numește frecvență de rotație. Adică câte revoluții reușește să facă punctul într-o secundă. Unghiul format din doi vectori cu rază se măsoară în radiani. Un radian este unghiul dintre doi vectori cu rază care taie un arc cu lungimea razei pe suprafața unui cerc.
Viteza unui punct care se deplasează în jurul unui cerc poate fi măsurată și în radiani pe secundă. În acest caz, mișcarea unui punct cu un radian pe secundă se numește viteză. Această viteză se numește viteză unghiulară. Adică, câte unități de unghi reușește vectorul rază să se rotească într-o secundă? Cu mișcare uniformă într-un cerc, viteza unghiulară este constantă.
Pentru a determina accelerația mișcării într-un cerc, trasăm în figură vectorii viteză ai punctelor A și B. Unghiul dintre acești vectori este egal cu unghiul dintre vectorii cu rază. Deoarece accelerația este diferența dintre vitezele luate într-un anumit interval de timp împărțit la acest interval. Apoi, folosind translația paralelă, vom transfera începutul vectorului viteză în punctul A în punctul B. Diferența dintre acești vectori va fi vectorul delta V. Dacă îl împărțim la coarda care leagă punctele A și B, cu condiția ca distanta dintre puncte este infinit mica, atunci vom obtine vectorul acceleratie indreptat catre centrul cercului. Care se mai numește și accelerație centripetă.
Când studiem mișcarea în fizică, conceptul de traiectorie joacă un rol important. Acesta este cel care determină în mare măsură tipul de mișcare a obiectelor și, în consecință, tipul de formule folosite pentru a descrie această mișcare. Una dintre traiectorii comune de mișcare este un cerc. În acest articol vom lua în considerare mișcarea centripetă atunci când ne mișcăm într-un cerc.
Conceptul de accelerație totală
Înainte de a caracteriza accelerația centripetă atunci când vă deplasați într-un cerc, să luăm în considerare conceptul de accelerație totală. Este considerată o mărime fizică care descrie simultan modificarea valorii absolute și a vectorului viteză. În formă matematică, această definiție arată astfel:
Accelerația este derivata totală a vitezei în raport cu timpul.
După cum se știe, viteza v¯ a corpului în fiecare punct al traiectoriei este direcționată de-a lungul unei tangente. Acest fapt ne permite să-l reprezentăm ca produs al modulului v și al vectorului tangent unitar u¯, adică:
Apoi se poate calcula după cum urmează:
a¯ = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt
Mărimea a¯ este suma vectorială a doi termeni. Primul termen este direcționat tangențial (ca viteza unui corp) și se numește Determină viteza de modificare a modulului de viteză. Al doilea termen - Să ne uităm la el mai detaliat mai târziu în articol.

Să scriem expresia de mai sus pentru componenta normală de accelerație a n ¯ în formă explicită:
a n ¯ = v*du¯/dt = v*du¯/dl*dl/dt = v 2 /r*r e ¯
Aici dl este calea parcursă de corp de-a lungul traiectoriei în timp dt, r e ¯ este vectorul unitar îndreptat către centrul de curbură al traiectoriei, r este raza de curbură. Formula rezultată conduce la câteva caracteristici importante ale componentei a n ¯ a accelerației totale:
- Mărimea a n ¯ crește pe măsură ce pătratul vitezei și scade invers proporțional cu raza, ceea ce o deosebește de componenta tangențială. Acesta din urmă nu este egal cu zero doar dacă modulul de viteză se schimbă.
- Accelerația normală este întotdeauna îndreptată spre centrul de curbură, motiv pentru care se numește centripetă.
Astfel, condiția principală pentru existența unei mărimi nenule a n ¯ este curbura traiectoriei. Dacă o astfel de curbură nu există (deplasare liniară), atunci a n ¯ = 0, deoarece r->∞.
Accelerație centripetă atunci când se deplasează într-un cerc

Un cerc este o linie geometrică, toate punctele care se află la aceeași distanță de un anumit punct. Acesta din urmă se numește centrul cercului, iar distanța menționată este raza acestuia. Dacă viteza unui corp în timpul rotației nu se modifică în valoare absolută, atunci vorbim de mișcare uniformă într-un cerc. Accelerația centripetă în acest caz poate fi calculată cu ușurință folosind una dintre cele două formule de mai jos:
Unde ω este viteza unghiulară, măsurată în radiani pe secundă (rad/s). A doua egalitate se obține datorită formulei pentru relația dintre vitezele unghiulare și cele liniare:
Forțe centripete și centrifuge
Când un corp se mișcă uniform într-un cerc, accelerația centripetă are loc datorită acțiunii forței centripete corespunzătoare. Vectorul său este întotdeauna îndreptat spre centrul cercului.
Natura acestei forțe poate fi foarte diversă. De exemplu, atunci când o persoană desface o piatră legată de o frânghie, aceasta este ținută în traiectoria sa de forța de întindere a frânghiei. Un alt exemplu de acțiune a forței centripete este interacțiunea gravitațională dintre Soare și planete. Acesta este ceea ce face ca toate planetele și asteroizii să se miște pe orbite circulare. Forța centripetă nu este capabilă să modifice energia cinetică a corpului, deoarece este direcționată perpendicular pe viteza sa.

Fiecare persoană ar putea observa că atunci când mașina se întoarce, de exemplu, spre stânga, pasagerii sunt apăsați pe marginea dreaptă a interiorului vehiculului. Acest proces este rezultatul forței centrifuge a mișcării de rotație. De fapt, această forță este ireală, deoarece se datorează proprietăților inerțiale ale corpului și dorinței sale de a se mișca pe o cale dreaptă.
Forțele centrifuge și centripete sunt egale ca mărime și opuse ca direcție. Dacă nu ar fi așa, atunci traiectoria circulară a corpului ar fi perturbată. Dacă luăm în considerare a doua lege a lui Newton, atunci putem spune că în timpul mișcării de rotație, accelerația centrifugă este egală cu accelerația centripetă.
Sursa locului de munca: Decizia 3553.-20. OGE 2016 Matematică, I.V. Iascenko. 36 de opțiuni.
Sarcina 18. Diagrama arată distribuția terenurilor pe categorii în districtele federale Ural, Volga, Sud și Orientul Îndepărtat. Determinați din diagramă care district are cea mai mică cotă de teren agricol.

1) Districtul Federal Ural
2) Districtul Federal Volga
3) Districtul Federal de Sud
4) Districtul Federal din Orientul Îndepărtat
Soluţie.
Terenurile agricole sunt colorate de un sector sub formă de linii orizontale (vezi figura). Trebuie să alegeți un district în care aria unui astfel de sector este minimă. Analiza figurii arată că acesta este Districtul Federal din Orientul Îndepărtat.
Răspuns: 4.
Sarcina 19. Bunica are 20 de cești: 10 cu flori roșii, restul cu albastre. Bunica toarnă ceaiul într-o ceașcă aleasă aleatoriu. Găsiți probabilitatea ca să fie o ceașcă cu flori albastre.
Soluţie.
Deoarece există exact 20-10 = 10 căni cu flori albastre și sunt 20 de căni în total, atunci probabilitatea de a alege o ceașcă cu flori albastre la întâmplare va fi egală cu
![]() .
.
Răspuns: 0,5.
Sarcina 20. Accelerația centripetă la mișcarea într-un cerc (în m/s2) poate fi calculată folosind formula a=w^2*R unde w este viteza unghiulară (în s-1) și R este raza cercului. Folosind această formulă, găsiți raza R (în metri) dacă viteza unghiulară este de 7,5 s-1 și accelerația centripetă este de 337,5 m/s2.
Soluţie.
Din formula pe care exprimăm raza cercului, obținem:
și calculați-l prin înlocuirea datelor , , în formula pe care o avem.
În natură, mișcarea corpului are loc adesea de-a lungul liniilor curbe. Aproape orice mișcare curbilinie poate fi reprezentată ca o succesiune de mișcări de-a lungul arcurilor circulare. În general, atunci când se deplasează într-un cerc, viteza unui corp se modifică ca in marime, deci si către.
Mișcare uniformă în jurul unui cerc
Mișcarea circulară se numește uniformă dacă viteza rămâne constantă.


Conform celei de-a treia legi a lui Newton, fiecare acțiune provoacă o reacție egală și opusă. Forța centripetă cu care conexiunea acționează asupra corpului este contracarată de o forță egală ca mărime și direcționată opus cu care corpul acționează asupra conexiunii. Această putere F 6 numit centrifugal,întrucât este îndreptată radial din centrul cercului. Forța centrifugă este egală ca mărime cu forța centripetă:
Exemple
Luați în considerare cazul în care un atlet rotește un obiect legat de capătul unei sfori în jurul capului său. Sportivul simte o forță aplicată pe braț și trăgându-l spre exterior. Pentru a ține obiectul pe cerc, sportivul (folosind un fir) îl trage spre interior. Prin urmare, conform celei de-a treia legi a lui Newton, un obiect (din nou printr-un fir) acţionează asupra mâinii cu o forţă egală şi opusă, iar aceasta este forţa pe care o simte mâna atletului (Fig. 3.23). Forța care acționează asupra unui obiect este tensiunea interioară a firului.

Un alt exemplu: un echipament sportiv „ciocan” este acţionat de un cablu ţinut de atlet (Fig. 3.24).

Să ne amintim că forța centrifugă nu acționează asupra unui corp în rotație, ci asupra unui fir. Dacă a acţionat forţa centrifugă pe corp atunci, dacă firul se rupe, acesta ar zbura radial departe de centru, așa cum se arată în Fig. 3.25, a. Totuși, de fapt, atunci când firul se rupe, corpul începe să se miște tangențial (Figura 3.25, b) în direcția vitezei pe care o avea în momentul ruperii firului.



O centrifugă este un dispozitiv conceput pentru antrenarea și testarea piloților, sportivilor și astronauților. Raza mare (până la 15 m) și puterea mare a motorului (câțiva MW) fac posibilă crearea unei accelerații centripete de până la 400 m/s 2 . Forța centrifugă presează corpurile cu o forță care depășește forța normală a gravitației pe Pământ de peste 40 de ori. O persoană poate rezista la o suprasarcină temporară de 20-30 de ori dacă stă perpendicular pe direcția forței centrifuge și de 6 ori dacă stă întinsă de-a lungul direcției acestei forțe.
3.8. Elemente de descriere a mișcării umane
Mișcările umane sunt complexe și greu de descris. Cu toate acestea, într-un număr de cazuri, este posibil să se identifice puncte semnificative care disting un tip de mișcare de altul. Luați în considerare, de exemplu, diferența dintre alergare și mers pe jos.
Elementele mișcărilor de pas la mers sunt prezentate în Fig. 3.26. În mișcările de mers, fiecare picior alternează între susținere și purtare. Perioada de sprijin include deprecierea (frânarea mișcării corpului către suport) și repulsie, în timp ce perioada de transfer include accelerația și frânarea.
Mișcările secvențiale ale corpului uman și ale picioarelor sale în timpul mersului sunt prezentate în Fig. 3.27.
Liniile A și B oferă o imagine de înaltă calitate a mișcării picioarelor în timpul mersului. Linia de sus A se referă la un picior, linia de jos B la celălalt. Secțiunile drepte corespund momentelor de sprijinire a picioarelor pe sol, secțiunile arcuite corespund momentelor de mișcare a picioarelor. Într-o perioadă de timp (a) ambele picioare se sprijină pe pământ; apoi (b)- piciorul A este în aer, piciorul B continuă să se încline; și apoi (Cu)- din nou ambele picioare se sprijină pe pământ. Cu cât mergi mai repede, cu atât intervalele devin mai scurte. (AȘi Cu).
În fig. Figura 3.28 prezintă mișcările secvențiale ale corpului uman la alergare și o reprezentare grafică a mișcărilor picioarelor. După cum puteți vedea în figură, atunci când rulați există intervale de timp { b, d, /), când ambele picioare sunt în aer și nu există intervale între picioarele care ating simultan solul. Aceasta este diferența dintre alergare și mers pe jos.
Un alt tip obișnuit de mișcare este împingerea de pe suport în timpul diferitelor sărituri. Împingerea se realizează prin îndreptarea piciorului de împingere și mișcări de balansare a brațelor și a trunchiului. Sarcina respingerii este de a asigura valoarea maximă a vectorului viteză inițială a centrului general de masă al sportivului și direcția optimă a acestuia. În fig. Sunt prezentate 3,29 faze

DINAMICĂ DE CONDUCEREPUNCTUL MATERIAL
Dinamica este o ramură a mecanicii care studiază mișcarea unui corp ținând cont de interacțiunea acestuia cu alte corpuri.
În secțiunea „Cinematică” au fost introduse conceptele vitezăȘi accelerare punct material. Pentru corpurile reale, aceste concepte au nevoie de clarificare, deoarece pentru diferite puncte reale ale corpului aceste caracteristici de mișcare pot varia. De exemplu, o minge de fotbal curbată nu numai că se mișcă înainte, ci și se rotește. Punctele unui corp în rotație se mișcă cu viteze diferite. Din acest motiv, se ia în considerare mai întâi dinamica unui punct material, iar apoi rezultatele obținute sunt extinse la corpuri reale.
Ne permite să existe pe această planetă. Cum putem înțelege ce este accelerația centripetă? Definiția acestei mărimi fizice este prezentată mai jos.
Observatii
Cel mai simplu exemplu de accelerație a unui corp care se mișcă într-un cerc poate fi observat prin rotirea unei pietre pe o frânghie. Tragi de frânghie, iar frânghia trage piatra spre centru. În fiecare moment de timp, frânghia conferă o anumită mișcare pietrei și de fiecare dată într-o nouă direcție. Vă puteți imagina mișcarea frânghiei ca o serie de smucituri slabe. O smucitură - și frânghia își schimbă direcția, o altă smucitură - o altă schimbare și așa mai departe într-un cerc. Dacă eliberați brusc frânghia, smucitura se va opri și, odată cu aceasta, schimbarea direcției de viteză se va opri. Piatra se va deplasa în direcția tangentă la cerc. Apare întrebarea: „Cu ce accelerație se va mișca corpul în acest moment?”
Formula pentru accelerația centripetă
În primul rând, este de remarcat faptul că mișcarea unui corp într-un cerc este complexă. Piatra participă simultan la două tipuri de mișcare: sub influența forței, se deplasează spre centrul de rotație și, în același timp, de-a lungul unei tangente la cerc, îndepărtându-se de acest centru. Conform celei de-a doua legi a lui Newton, forța care ține o piatră pe o frânghie este îndreptată spre centrul de rotație de-a lungul frânghiei. Tot acolo va fi direcționat vectorul accelerație.
Să presupunem că după ceva timp piatra noastră, mișcându-se uniform cu viteza V, ajunge din punctul A în punctul B. Să presupunem că în momentul în care corpul a traversat punctul B, forța centripetă a încetat să mai acționeze asupra lui. Apoi, într-o perioadă de timp, ar ajunge la punctul K. Se află pe tangentă. Dacă în același moment de timp ar acționa asupra corpului doar forțe centripete, atunci în timpul t, mișcându-se cu aceeași accelerație, acesta ar ajunge în punctul O, care se află pe o dreaptă reprezentând diametrul unui cerc. Ambele segmente sunt vectori și respectă regula adunării vectoriale. Ca urmare a însumării acestor două mișcări pe o perioadă de timp t, obținem mișcarea rezultată de-a lungul arcului AB.

Dacă intervalul de timp t este considerat a fi neglijabil mic, atunci arcul AB va diferi puțin de coarda AB. Astfel, este posibil să înlocuiți mișcarea de-a lungul unui arc cu mișcarea de-a lungul unei coarde. În acest caz, mișcarea pietrei de-a lungul coardei va respecta legile mișcării rectilinie, adică distanța parcursă AB va fi egală cu produsul dintre viteza pietrei și timpul mișcării sale. AB = V x t.
Să notăm accelerația centripetă dorită cu litera a. Apoi, calea parcursă numai sub influența accelerației centripete poate fi calculată folosind formula pentru mișcarea accelerată uniform:
Distanța AB este egală cu produsul dintre viteză și timp, adică AB = V x t,
AO - calculat mai devreme folosind formula mișcării uniform accelerate pentru deplasarea în linie dreaptă: AO = la 2 / 2.
Înlocuind aceste date în formulă și transformând-o, obținem o formulă simplă și elegantă pentru accelerația centripetă:
În cuvinte, aceasta poate fi exprimată după cum urmează: accelerația centripetă a unui corp care se mișcă într-un cerc este egală cu câtul vitezei liniare la pătrat de raza cercului de-a lungul căruia corpul se rotește. Forța centripetă în acest caz va arăta ca în imaginea de mai jos.

Viteză unghiulară
Viteza unghiulară este egală cu viteza liniară împărțită la raza cercului. Afirmația inversă este de asemenea adevărată: V = ωR, unde ω este viteza unghiulară
Dacă înlocuim această valoare în formulă, putem obține o expresie pentru accelerația centrifugă pentru viteza unghiulară. Va arata asa:
Accelerație fără schimbarea vitezei
Și totuși, de ce un corp cu accelerație îndreptată spre centru nu se mișcă mai repede și se apropie de centrul de rotație? Răspunsul constă în formularea însăși a accelerației. Faptele arată că mișcarea circulară este reală, dar pentru a o menține este nevoie de o accelerație îndreptată spre centru. Sub influența forței cauzate de această accelerație, are loc o modificare a cantității de mișcare, în urma căreia traiectoria mișcării este constant curbată, tot timpul schimbând direcția vectorului viteză, dar fără a modifica valoarea absolută a acestuia. . Mișcându-se în cerc, piatra noastră îndelungată de suferință se repezi spre interior, altfel ar continua să se miște tangențial. În fiecare moment de timp, mergând tangenţial, piatra este atrasă de centru, dar nu cade în el. Un alt exemplu de accelerare centripetă ar fi un schior de apă care face cercuri mici pe apă. Silueta atletului este înclinată; pare să cadă, continuând să se miște și aplecându-se înainte.

Astfel, putem concluziona că accelerația nu crește viteza corpului, deoarece vectorii viteză și accelerație sunt perpendiculari unul pe celălalt. Adăugată la vectorul viteză, accelerația schimbă doar direcția de mișcare și menține corpul pe orbită.
Depășirea factorului de siguranță
În experimentul anterior aveam de-a face cu o frânghie perfectă care nu s-a rupt. Dar să presupunem că frânghia noastră este cea mai obișnuită și puteți chiar să calculați forța după care se va rupe pur și simplu. Pentru a calcula această forță, este suficient să comparăm rezistența frânghiei cu sarcina pe care o experimentează în timpul rotației pietrei. Prin rotirea pietrei cu o viteză mai mare, îi oferiți o mișcare mai mare și, prin urmare, o accelerație mai mare.

Cu un diametru de frânghie de iută de aproximativ 20 mm, rezistența sa la tracțiune este de aproximativ 26 kN. Este de remarcat faptul că lungimea frânghiei nu apare nicăieri. Prin rotirea unei sarcini de 1 kg pe o frânghie cu raza de 1 m, putem calcula că viteza liniară necesară ruperii acesteia este de 26 x 10 3 = 1 kg x V 2 / 1 m. Astfel, viteza care este periculoasă pentru depășirea va fi egală cu √ 26 x 10 3 = 161 m/s.
Gravitatie
Când luăm în considerare experimentul, am neglijat efectul gravitației, deoarece la viteze atât de mari influența sa este neglijabilă. Dar puteți observa că atunci când desfășurați o frânghie lungă, corpul descrie o traiectorie mai complexă și se apropie treptat de sol.
Corpuri cerești
Dacă transferăm legile mișcării circulare în spațiu și le aplicăm mișcării corpurilor cerești, putem redescoperi mai multe formule de mult familiare. De exemplu, forța cu care un corp este atras de Pământ este cunoscută prin formula:
În cazul nostru, factorul g este aceeași accelerație centripetă care a fost derivată din formula anterioară. Numai în acest caz, rolul pietrei va fi jucat de un corp ceresc atras de Pământ, iar rolul frânghiei va fi jucat de forța gravitației. Factorul g va fi exprimat în termeni de raza planetei noastre și viteza de rotație a acesteia.

Rezultate
Esența accelerației centripete este munca grea și ingrată de a menține un corp în mișcare pe orbită. Se observă un caz paradoxal când, cu o accelerație constantă, un corp nu își modifică valoarea vitezei. Pentru mintea neantrenată, o astfel de afirmație este destul de paradoxală. Cu toate acestea, atât atunci când se calculează mișcarea unui electron în jurul nucleului, cât și când se calculează viteza de rotație a unei stele în jurul unei găuri negre, accelerația centripetă joacă un rol important.