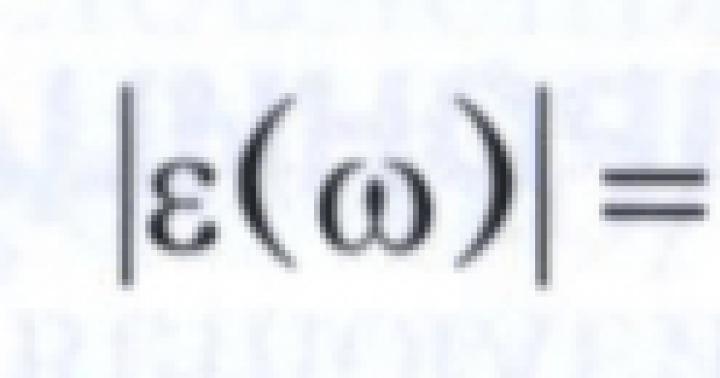Înainte de a trece la subiectul articolului, amintim conceptele de bază.
Definiția 1
Vector- un segment de linie dreaptă caracterizat printr-o valoare și direcție numerică. Un vector este notat printr-o literă latină minusculă cu o săgeată în partea de sus. Dacă există puncte de limită specifice, desemnarea vectorului arată ca două litere mari latine (marcând limitele vectorului), de asemenea, cu o săgeată deasupra.
Definiția 2
Vector zero- orice punct al planului, notat cu zero cu o săgeată deasupra.
Definiția 3
Lungimea vectorului- o valoare egală sau mai mare decât zero, care determină lungimea segmentului care alcătuiește vectorul.
Definiția 4
Vectori coliniari- culcat pe o linie sau pe linii paralele. Vectorii care nu îndeplinesc această condiție se numesc necoliniari.
Definiția 5Intrare: Vectori a →și b →. Pentru a efectua operația de adăugare asupra lor, este necesar să amânați vectorul dintr-un punct arbitrar A B →, egal cu vectorul a →; din punctul primit nedefinit - vector În C →, egal cu vectorul b →. Conectând punctele nedefinite și C , obținem un segment (vector) A C →, care va fi suma datelor originale. În caz contrar, se numește schema de adunare vectorială descrisă regula triunghiului.
Din punct de vedere geometric, adăugarea vectorială arată astfel:
Pentru vectori necoliniari:
Pentru vectori coliniari (codirecționali sau opuși):

Luând ca bază schema descrisă mai sus, avem ocazia de a efectua operația de a adăuga mai mult de 2 vectori: adăugând fiecare vector ulterior pe rând.
Definiția 6
Intrare: Vectori a → , b → , c →, d → . Dintr-un punct arbitrar A pe plan, este necesar să se lase deoparte un segment (vector) egal cu vectorul a →; apoi, de la sfârșitul vectorului rezultat, un vector egal cu vectorul b →; în continuare - vectorii următori sunt amânați după același principiu. Punctul final al ultimului vector amânat va fi punctul B , iar segmentul rezultat (vector) A B →- suma tuturor datelor inițiale. Se mai numește schema descrisă pentru adăugarea mai multor vectori regula poligonului .
Geometric, arată astfel:

Definiția 7
O schemă separată de acțiune pentru scădere vectorială nu, pentru că de fapt diferenţa de vectori a →și b → este suma vectorilor a →și - b → .
Definiția 8Pentru a efectua acțiunea de înmulțire a unui vector cu un anumit număr k, trebuie luate în considerare următoarele reguli:
- dacă k > 1, atunci acest număr va întinde vectorul de k ori;
-daca 0< k < 1 , то это число приведет к сжатию вектора в
de 1k ori;
- dacă k< 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
- daca k = 1 , atunci vectorul ramane acelasi;
- dacă unul dintre factori este un vector zero sau un număr egal cu zero, rezultatul înmulțirii va fi un vector zero.
Date inițiale:
1) vector a → iar numărul k = 2;
2) vector b → iar numărul k = - 1 3 .
Din punct de vedere geometric, rezultatul înmulțirii în conformitate cu regulile de mai sus va arăta astfel:

Operațiile pe vectori descrise mai sus au proprietăți, dintre care unele sunt evidente, în timp ce altele pot fi justificate geometric.
Intrare: Vectori a → , b → , c →și numere reale arbitrare λ și μ.

Proprietățile comutativității și asociativității fac posibilă adăugarea vectorilor într-o ordine arbitrară.
Proprietățile enumerate ale operațiilor permit efectuarea transformărilor necesare ale expresiilor vector-numerice similare cu cele numerice obișnuite. Să ne uităm la asta cu un exemplu.
Exemplul 1
Sarcină: simplificați expresia a → - 2 (b → + 3 a →)
Decizie
- folosind a doua proprietate distributivă, obținem: a → - 2 (b → + 3 a →) = a → - 2 b → - 2 (3 a →)
- folosiți proprietatea asociativă a înmulțirii, expresia va lua următoarea formă: a → - 2 b → - 2 (3 a →) = a → - 2 b → - (2 3) a → = a → - 2 b → - 6 a →
- folosind proprietatea comutativității, schimbăm termenii: a → - 2 b → - 6 a → = a → - 6 a → - 2 b →
- atunci, conform primei proprietăți de distribuție, obținem: a → - 6 a → - 2 b → = (1 - 6) a → - 2 b → = - 5 a → - 2 b → O scurtă înregistrare a soluției va arăta astfel: a → - 2 (b → + 3 a →) = a → - 2 b → - 2 3 a → = 5 a → - 2 b →
Răspuns: a → - 2 (b → + 3 a →) = - 5 a → - 2 b →
Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter
Pagina 1 din 2
Intrebarea 1. Ce este un vector? Cum sunt definiți vectorii?
Răspuns. Vom numi un segment dirijat un vector (Fig. 211). Direcția unui vector este determinată prin specificarea începutului și sfârșitului acestuia. În desen, direcția vectorului este marcată cu o săgeată. Pentru a desemna vectorii, vom folosi literele latine mici a, b, c, ... . De asemenea, puteți desemna un vector specificând începutul și sfârșitul acestuia. În acest caz, începutul vectorului este plasat pe primul loc. În loc de cuvântul „vector”, o săgeată sau o liniuță este uneori plasată deasupra desemnării literei vectorului. Vectorul din figura 211 poate fi notat astfel:
\(\overline(a)\), \(\overrightarrow(a)\) sau \(\overline(AB)\), \(\overrightarrow(AB)\).
Intrebarea 2. Ce vectori sunt numiți egal direcționați (direcționați opus)?
Răspuns. Se spune că vectorii \(\overline(AB)\) și \(\overline(CD)\) sunt egal direcționați dacă semiliniile AB și CD sunt egal direcționate.
Vectorii \(\overline(AB)\) și \(\overline(CD)\) se numesc direcționați opus dacă semidreptele AB și CD sunt direcționate opus.
În Figura 212, vectorii \(\overline(a)\) și \(\overline(b)\) au aceeași direcție, în timp ce vectorii \(\overline(a)\) și \(\overline(c) \) au direcții opuse.

Întrebarea 3. Care este valoarea absolută a unui vector?
Răspuns. Valoarea absolută (sau modulul) unui vector este lungimea segmentului care reprezintă vectorul. Valoarea absolută a vectorului \(\overline(a)\) se notează cu |\(\overline(a)\)|.
Întrebarea 4. Ce este un vector nul?
Răspuns.Începutul unui vector poate coincide cu sfârșitul acestuia. Un astfel de vector va fi numit vector zero. Vectorul zero este notat cu zero cu o liniuță (\(\overline(0)\)). Nimeni nu vorbește despre direcția vectorului zero. Valoarea absolută a vectorului zero este considerată egală cu zero.
Întrebarea 5. Ce vectori se numesc egali?
Răspuns. Se spune că doi vectori sunt egali dacă sunt combinați printr-o translație paralelă. Aceasta înseamnă că există o translație paralelă care mută începutul și sfârșitul unui vector la începutul și, respectiv, sfârșitul altui vector.
Întrebarea 6. Demonstrați că vectorii egali au aceeași direcție și sunt egali în valoare absolută. Și invers: vectorii egal direcționați care sunt egali în valoare absolută sunt egali.
Răspuns. Cu translația paralelă, vectorul își păstrează direcția, precum și valoarea sa absolută. Aceasta înseamnă că vectorii egali au aceeași direcție și sunt egali în valoare absolută.
Fie \(\overline(AB)\) și \(\overline(CD)\) să fie vectori egal direcționați egali în valoare absolută (Fig. 213). O translație paralelă care duce punctul C la punctul A combină semi-linia CD cu semi-linia AB, deoarece acestea sunt în mod egal direcționate. Și întrucât segmentele AB și CD sunt egale, atunci punctul D coincide cu punctul B, adică. translația paralelă traduce vectorul \(\overline(CD)\) în vectorul \(\overline(AB)\). Prin urmare, vectorii \(\overline(AB)\) și \(\overline(CD)\) sunt egali, după cum este necesar.

Întrebarea 7. Demonstrați că din orice punct se poate desena un vector egal cu vectorul dat și numai unul.
Răspuns. Fie CD o linie și vectorul \(\overline(CD)\) să fie o parte a liniei CD. Fie AB linia în care intră linia CD în timpul translației paralele, \(\overline(AB)\) să fie vectorul în care intră vectorul \(\overline(CD)\) în timpul translației paralele și, prin urmare, vectorii \(\ overline(AB)\) și \(\overline(CD)\) sunt egale, iar liniile AB și CD sunt paralele (vezi Fig. 213). După cum știm, printr-un punct care nu se află pe o dreaptă dată, este posibil să se deseneze pe plan cel mult o dreaptă paralelă cu cea dată (axioma dreptelor paralele). Prin urmare, prin punctul A se poate trasa o dreaptă paralelă cu dreapta CD. Deoarece vectorul \(\overline(AB)\) face parte din dreapta AB, este posibil să se deseneze un vector \(\overline(AB)\) prin punctul A, care este egal cu vectorul \(\overline (CD)\).
Întrebarea 8. Ce sunt coordonatele vectoriale? Care este valoarea absolută a vectorului cu coordonatele a 1 , a 2 ?
Răspuns. Fie vectorul \(\overline(a)\) să înceapă în punctul A 1 (x 1 ; y 1) și se termină în punctul A 2 (x 2 ; y 2). Coordonatele vectorului \(\overline(a)\) vor fi numerele a 1 = x 2 - x 1 , a 2 = y 2 - y 1 . Vom pune coordonatele vectorului lângă desemnarea literei vectorului, în acest caz \(\overline(a)\) (a 1 ; a 2) sau doar \((\overline(a 1 ; a 2 ))\ ). Coordonatele vectorului zero sunt egale cu zero.
Din formula care exprimă distanța dintre două puncte în funcție de coordonatele lor, rezultă că valoarea absolută a vectorului cu coordonatele a 1 , a 2 este \(\sqrt(a^2 1 + a^2 2 )\).
Întrebarea 9. Demonstrați că vectorii egali au coordonate egale, iar vectorii cu coordonate egale sunt egali.
Răspuns. Fie A 1 (x 1 ; y 1) și A 2 (x 2 ; y 2) începutul și sfârșitul vectorului \(\overline(a)\). Deoarece vectorul \(\overline(a")\) egal cu acesta se obține din vectorul \(\overline(a)\) prin translație paralelă, atunci începutul și sfârșitul acestuia vor fi respectiv A" 1 (x 1 + c ; y 1 + d ), A" 2 (x 2 + c; y 2 + d). Aceasta arată că ambii vectori \(\overline(a)\) și \(\overline(a")\) au aceleași coordonate: x 2 - x 1 , y 2 - y 1 .
Să demonstrăm acum afirmația inversă. Fie coordonatele corespunzătoare ale vectorilor \(\overline(A 1 A 2 )\) și \(\overline(A" 1 A" 2 )\) să fie egale. Demonstrăm că vectorii sunt egali.
Fie x" 1 și y" 1 coordonatele punctului A" 1 și x" 2, y" 2 coordonatele punctului A" 2. Prin condiția teoremei x 2 - x 1 \u003d x "2 - x" 1, y 2 - y 1 \u003d y "2 - y" 1. Prin urmare, x "2 = x 2 + x" 1 - x 1, y" 2 = y 2 + y" 1 - y 1. Translația paralelă dată de formule
x" = x + x" 1 - x 1, y" = y + y" 1 - y 1,
transferă punctul A 1 în punctul A" 1 , iar punctul A 2 în punctul A" 2 , adică. vectorii \(\overline(A 1 A 2 )\) și \(\overline(A" 1 A" 2 )\) sunt egali, după cum este necesar.
Întrebarea 10. Definiți suma vectorilor.
Răspuns. Suma vectorilor \(\overline(a)\) și \(\overline(b)\) cu coordonatele a 1 , a 2 și b 1 , b 2 este vectorul \(\overline(c)\) cu coordonatele a 1 + b 1 , a 2 + b a 2 , adică.
\(\overline(a) (a 1 ; a 2) + \overline(b)(b 1 ; b 2) = \overline(c) (a 1 + b 1 ; a 2 + b 2)\).
Vectorul \(\overrightarrow(AB)\) poate fi văzut ca mișcând un punct din poziția \(A\) (începutul mișcării) în poziția \(B\) (sfârșitul mișcării). Adică traiectoria mișcării în acest caz nu este importantă, doar începutul și sfârșitul sunt importante!
\(\blacktriangleright\) Doi vectori sunt coliniari dacă se află pe aceeași dreaptă sau pe două drepte paralele.
În caz contrar, vectorii sunt numiți necoliniari.
\(\blacktriangleright\) Se spune că doi vectori coliniari sunt codirecționali dacă direcțiile lor sunt aceleași.
Dacă direcțiile lor sunt opuse, atunci ele sunt numite direcționate opus.
Reguli pentru adăugarea vectorilor coliniari:
co-directional Sfârşit primul. Apoi suma lor este un vector, începutul căruia coincide cu începutul primului vector, iar sfârșitul coincide cu sfârșitul celui de-al doilea (Fig. 1).
\(\blacktriangleright\) Pentru a adăuga două directii opuse vector, puteți amâna al doilea vector de la start primul. Atunci suma lor este un vector, al cărui început coincide cu începutul ambilor vectori, lungimea este egală cu diferența de lungimi ale vectorilor, direcția coincide cu direcția vectorului mai lung (Fig. 2).

Reguli pentru adăugarea vectorilor necoliniari \(\overrightarrow (a)\) și \(\overrightarrow(b)\) :
\(\blacktriangleright\) Regula triunghiului (Fig. 3).
Este necesar să amânați vectorul \(\overrightarrow (b)\) de la sfârșitul vectorului \(\overrightarrow (a)\) . Atunci suma este un vector al cărui început coincide cu începutul vectorului \(\overrightarrow (a)\) și al cărui sfârșit coincide cu sfârșitul vectorului \(\overrightarrow (b)\) .
\(\blacktriangleright\) Regula paralelogramului (Fig. 4).
Este necesar să amânați vectorul \(\overrightarrow (b)\) de la începutul vectorului \(\overrightarrow (a)\) . Apoi suma \(\overrightarrow (a)+\overrightarrow (b)\) este un vector care coincide cu diagonala paralelogramului construit pe vectorii \(\overrightarrow (a)\) și \(\overrightarrow (b)\) (al cărui început coincide cu începutul ambilor vectori).
\(\blacktriangleright\) Pentru a găsi diferența dintre doi vectori \(\overrightarrow(a)-\overrightarrow(b)\), trebuie să găsiți suma vectorilor \(\overrightarrow (a)\) și \(-\overrightarrow(b)\) : \(\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\)(Fig. 5).

Sarcina 1 #2638
Nivel de sarcină: Mai dificil decât examenul
Având în vedere un triunghi dreptunghic \(ABC\) cu un unghi drept \(A\) , punctul \(O\) este centrul cercului circumscris în jurul triunghiului dat. Coordonatele vectoriale \(\overrightarrow(AB)=\(1;1\)\), \(\overrightarrow(AC)=\(-1;1\)\). Aflați suma coordonatelor vectorului \(\overrightarrow(OC)\) .
pentru că triunghiul \(ABC\) este dreptunghic, apoi centrul cercului circumscris se află în mijlocul ipotenuzei, adică. \(O\) este mijlocul lui \(BC\) .

observa asta \(\overrightarrow(BC)=\overrightarrow(AC)-\overrightarrow(AB)\), prin urmare, \(\overrightarrow(BC)=\(-1-1;1-1\)=\(-2;0\)\).
pentru că \(\overrightarrow(OC)=\dfrac12 \overrightarrow(BC)\), apoi \(\overrightarrow(OC)=\(-1;0\)\).
Prin urmare, suma coordonatelor vectorului \(\overrightarrow(OC)\) este egală cu \(-1+0=-1\) .
Raspunsul 1
Sarcina 2 #674
Nivel de sarcină: Mai dificil decât examenul
\(ABCD\) este un patrulater ale cărui laturi conțin vectorii \(\overrightarrow(AB)\) , \(\overrightarrow(BC)\) , \(\overrightarrow(CD)\) , \(\overrightarrow(DA) \) . Aflați lungimea vectorului \(\overrightarrow(AB) + \overrightarrow(BC) + \overrightarrow(CD) + \overrightarrow(DA)\).

\(\overrightarrow(AB) + \overrightarrow(BC) = \overrightarrow(AC)\), \(\overrightarrow(AC) + \overrightarrow(CD) = \overrightarrow(AD)\), apoi
\(\overrightarrow(AB) + \overrightarrow(BC) + \overrightarrow(CD) + \overrightarrow(DA) = \overrightarrow(AC) + \overrightarrow(CD) + \overrightarrow(DA)= \overrightarrow(AD) + \overrightarrow(DA) = \overrightarrow(AD) - \overrightarrow(AD) = \vec(0)\).
Vectorul nul are lungimea egală cu \(0\) .
Un vector poate fi gândit ca o deplasare, atunci \(\overrightarrow(AB) + \overrightarrow(BC)\)- trece de la \(A\) la \(B\) , iar apoi de la \(B\) la \(C\) - în cele din urmă este o mutare de la \(A\) la \(C\) .
Cu această interpretare, devine clar că \(\overrightarrow(AB) + \overrightarrow(BC) + \overrightarrow(CD) + \overrightarrow(DA) = \vec(0)\), deoarece ca urmare, aici ne-am mutat din punctul \(A\) în punctul \(A\) , adică lungimea unei astfel de mișcări este egală cu \(0\) , ceea ce înseamnă că vectorul de o astfel de mișcare în sine este \(\vec(0)\) .
Raspuns: 0
Sarcina 3 #1805
Nivel de sarcină: Mai dificil decât examenul
Dat un paralelogram \(ABCD\) . Diagonalele \(AC\) și \(BD\) se intersectează în punctul \(O\) . Lasă, atunci \(\overrightarrow(OA) = x\cdot\vec(a) + y\cdot\vec(b)\)

\[\overrightarrow(OA) = \frac(1)(2)\overrightarrow(CA) = \frac(1)(2)(\overrightarrow(CB) + \overrightarrow(BA)) = \frac(1)( 2)(\overrightarrow(DA) + \overrightarrow(BA)) = \frac(1)(2)(-\vec(b) - \vec(a)) = - \frac(1)(2)\vec (a) - \frac(1)(2)\vec(b)\]\(\Rightarrow\) \(x = - \frac(1)(2)\) , \(y = - \frac(1)(2)\) \(\Rightarrow\) \(x + y = - unu\) .
Raspunsul 1
Sarcina 4 #1806
Nivel de sarcină: Mai dificil decât examenul
Dat un paralelogram \(ABCD\) . Punctele \(K\) și \(L\) se află pe laturile \(BC\) și, respectiv, \(CD\), și \(BK:KC = 3:1\) și \(L\) este punctul de mijloc \ (CD\) . Lasa \(\overrightarrow(AB) = \vec(a)\), \(\overrightarrow(AD) = \vec(b)\), apoi \(\overrightarrow(KL) = x\cdot\vec(a) + y\cdot\vec(b)\), unde \(x\) și \(y\) sunt câteva numere. Aflați numărul egal cu \(x + y\) .

\[\overrightarrow(KL) = \overrightarrow(KC) + \overrightarrow(CL) = \frac(1)(4)\overrightarrow(BC) + \frac(1)(2)\overrightarrow(CD) = \frac (1)(4)\overrightarrow(AD) + \frac(1)(2)\overrightarrow(BA) = \frac(1)(4)\vec(b) - \frac(1)(2)\vec (A)\]\(\Rightarrow\) \(x = -\frac(1)(2)\) , \(y = \frac(1)(4)\) \(\Rightarrow\) \(x + y = -0 ,25\) .
Răspuns: -0,25
Sarcina 5 #1807
Nivel de sarcină: Mai dificil decât examenul
Dat un paralelogram \(ABCD\) . Punctele \(M\) și \(N\) se află pe laturile \(AD\) și respectiv \(BC\), unde \(AM:MD = 2:3\) și \(BN:NC = 3 ): unul\) . Lasa \(\overrightarrow(AB) = \vec(a)\), \(\overrightarrow(AD) = \vec(b)\), apoi \(\overrightarrow(MN) = x\cdot\vec(a) + y\cdot\vec(b)\)

\[\overrightarrow(MN) = \overrightarrow(MA) + \overrightarrow(AB) + \overrightarrow(BN) = \frac(2)(5)\overrightarrow(DA) + \overrightarrow(AB) + \frac(3) )(4)\overrightarrow(BC) = - \frac(2)(5)\overrightarrow(AD) + \overrightarrow(AB) + \frac(3)(4)\overrightarrow(BC) = -\frac(2 )(5)\vec(b) + \vec(a) + \frac(3)(4)\vec(b) = \vec(a) + \frac(7)(20)\vec(b)\ ]\(\Rightarrow\) \(x = 1\) , \(y = \frac(7)(20)\) \(\Rightarrow\) \(x\cdot y = 0,35\) .
Răspuns: 0,35
Sarcina 6 #1808
Nivel de sarcină: Mai dificil decât examenul
Dat un paralelogram \(ABCD\) . Punctul \(P\) se află pe diagonala \(BD\), punctul \(Q\) se află pe latura \(CD\) , unde \(BP:PD = 4:1\) și \( CQ:QD = 1:9 \). Lasa \(\overrightarrow(AB) = \vec(a)\), \(\overrightarrow(AD) = \vec(b)\), apoi \(\overrightarrow(PQ) = x\cdot\vec(a) + y\cdot\vec(b)\), unde \(x\) și \(y\) sunt câteva numere. Găsiți numărul egal cu \(x\cdot y\) .

\[\begin(gathered) \overrightarrow(PQ) = \overrightarrow(PD) + \overrightarrow(DQ) = \frac(1)(5)\overrightarrow(BD) + \frac(9)(10)\overrightarrow( DC) = \frac(1)(5)(\overrightarrow(BC) + \overrightarrow(CD)) + \frac(9)(10)\overrightarrow(AB) =\\ = \frac(1)(5) (\overrightarrow(AD) + \overrightarrow(BA)) + \frac(9)(10)\overrightarrow(AB) = \frac(1)(5)(\overrightarrow(AD) - \overrightarrow(AB)) + \frac(9)(10)\overrightarrow(AB) = \frac(1)(5)\overrightarrow(AD) + \frac(7)(10)\overrightarrow(AB) = \frac(1)(5) \vec(b) + \frac(7)(10)\vec(a)\end(adunat)\]
\(\Rightarrow\) \(x = \frac(7)(10)\) , \(y = \frac(1)(5)\) \(\Rightarrow\) \(x\cdot y = 0, paisprezece\) . iar \(ABCO\) este un paralelogram; \(AF \parallel BE\) și \(ABOF\) – paralelogram \(\Rightarrow\) \[\overrightarrow(BC) = \overrightarrow(AO) = \overrightarrow(AB) + \overrightarrow(BO) = \overrightarrow(AB) + \overrightarrow(AF) = \vec(a) + \vec(b)\ ]\(\Rightarrow\) \(x = 1\) , \(y = 1\) \(\Rightarrow\) \(x + y = 2\) .
Raspuns: 2
Liceenii care se pregătesc pentru examenul de matematică și în același timp se bazează pe obținerea unor note decente trebuie să repete cu siguranță subiectul „Reguli pentru adunarea și scăderea mai multor vectori”. După cum se poate observa din mulți ani de practică, astfel de sarcini sunt incluse în testul de certificare în fiecare an. Dacă un absolvent are dificultăți cu sarcinile din secțiunea „Geometrie pe un plan”, de exemplu, în care este necesar să aplice regulile de adunare și scădere a vectorilor, ar trebui cu siguranță să repete sau să reînțeleagă materialul pentru a putea cu succes. promovarea examenului.
Proiectul educațional „Shkolkovo” oferă o nouă abordare a pregătirii pentru testul de certificare. Resursa noastră este construită în așa fel încât elevii să poată identifica cele mai dificile secțiuni pentru ei înșiși și să umple golurile de cunoștințe. Specialiștii Shkolkovo au pregătit și sistematizat tot materialul necesar pentru pregătirea testului de certificare.
Pentru ca sarcinile USE, în care este necesară aplicarea regulilor de adunare și scădere a doi vectori, să nu creeze dificultăți, vă recomandăm să reîmprospătați în primul rând conceptele de bază din memorie. Studenții pot găsi acest material în secțiunea „Referință teoretică”.
Dacă v-ați amintit deja regula de scădere a vectorilor și definițiile de bază pe acest subiect, vă sugerăm să vă consolidați cunoștințele completând exercițiile adecvate care au fost selectate de specialiștii portalului educațional Shkolkovo. Pentru fiecare problemă, site-ul prezintă un algoritm de soluție și oferă răspunsul corect. Subiectul Reguli de adăugare a vectorilor conține diverse exerciții; după finalizarea a două sau trei sarcini relativ ușoare, elevii pot trece succesiv la altele mai dificile.
Să-și perfecționeze propriile abilități în astfel de sarcini, de exemplu, deoarece școlarii au posibilitatea online, fiind la Moscova sau în orice alt oraș din Rusia. Dacă este necesar, sarcina poate fi salvată în secțiunea „Favorite”. Datorită acestui fapt, puteți găsi rapid exemple de interes și puteți discuta cu profesorul despre algoritmii pentru găsirea răspunsului corect.
Unele mărimi fizice, de exemplu, forța sau viteza, sunt caracterizate nu numai de o valoare numerică, ci și de direcție. Astfel de mărimi se numesc mărimi vectoriale: F⃗ - puterea, v⃗ - viteza.
Să dăm o definiție geometrică a unui vector.
Vector
se numește un segment, pentru care se indică care dintre punctele sale de limită este considerat început și care este sfârșitul.
În desene, un vector este reprezentat ca un segment de linie cu o săgeată care indică sfârșitul vectorului. Un vector este notat cu două litere mari latine cu o săgeată deasupra lor. Prima literă indică începutul vectorului, a doua - sfârșitul.
Un vector poate fi de asemenea notat printr-o singură literă latină minusculă cu o săgeată deasupra sa.
Lungimea unui vector este lungimea segmentului care reprezintă acest vector. Parantezele verticale sunt folosite pentru a indica lungimea unui vector.
Se numește un vector al cărui sfârșit este același cu începutul zero
vector. Vectorul zero este reprezentat printr-un punct și este notat cu două litere identice sau zero cu o săgeată deasupra acestuia. Lungimea vectorului zero este egală cu zero: |0 ⃗|= 0.
Să introducem conceptul coliniare vectori. Vectorii nenuli sunt numiți coliniari dacă se află pe aceeași linie sau pe linii paralele. Vectorul zero este considerat coliniar cu orice vector.
Dacă vectorii coliniari nenuli au aceeași direcție, atunci astfel de vectori vor fi codirecționali. Dacă direcțiile lor sunt opuse, ele se numesc direcționate opus.
Există notații speciale pentru desemnarea vectorilor co-direcționați și direcționați opus:
- m ⃗ R⃗ dacă vectorii m⃗ și R⃗ co-regizat;
- m ⃗ ↓ n⃗ dacă vectorii m⃗ și n⃗ Dirijată opus.
Luați în considerare mișcarea unei mașini. Viteza fiecăruia dintre punctele sale este o mărime vectorială și este reprezentată de un segment direcționat. Deoarece toate punctele mașinii se mișcă cu aceeași viteză, toate segmentele direcționate care reprezintă vitezele diferitelor puncte au aceeași direcție și lungimile lor sunt egale. Acest exemplu ne oferă un indiciu despre cum să determinăm dacă vectorii sunt egali.
Se spune că doi vectori sunt egali dacă sunt în aceeași direcție și lungimile lor sunt egale. Egalitatea vectorilor se poate scrie folosind semnul egal: A ⃗ = b ⃗, KH ⃗ = OE ⃗
Dacă punct R pornire vectorială R⃗, atunci considerăm că vectorul R⃗ amânat de la punct R.
Să demonstrăm asta din orice punct O puteți pune deoparte un vector egal cu un vector dat R⃗ și numai unul.
Dovada:
1) Dacă R⃗ este vectorul zero, atunci OO ⃗ = R ⃗.
2) Dacă vectorul R⃗ diferit de zero, punct R este începutul acestui vector și punctul T- sfarsit.
Treceți prin punct O drept, paralel RT. Pe linia dreaptă construită, punem deoparte segmentele OA 1 și OA 2 egal cu segmentul RT.
Alegeți dintre vectori OA 1 și OA 2 vector care este co-directional cu vectorul R⃗. În desenul nostru, acesta este un vector OA unu . Acest vector va fi egal cu vectorul R⃗. Din construcție rezultă că un astfel de vector este unic.
Cunoștințele și abilitățile dobândite în această lecție vor fi utile studenților nu numai la lecțiile de geometrie, ci și la orele de alte științe. În timpul lecției, elevii vor învăța cum să traseze un vector dintr-un punct dat. Poate fi o lecție obișnuită de geometrie, precum și o oră de matematică extracurriculară sau extracurriculară. Această dezvoltare îl va ajuta pe profesor să-și economisească timpul pregătindu-se pentru lecția cu tema „Întârzierea unui vector dintr-un punct dat”. Va fi suficient pentru el să joace lecția video în clasă și apoi să consolideze materialul cu propria sa selecție de exerciții.
Durata lecției durează doar 1:44 minute. Dar acest lucru este suficient pentru a-i învăța pe școlari să amâne vectorul dintr-un punct dat.
Lecția începe cu o demonstrație a unui vector al cărui început este la un moment dat. Ei spun că vectorul este amânat de la el. Atunci autorul își propune să se demonstreze cu el aserțiunea conform căreia se poate trage din orice punct un vector egal cu cel dat și, în plus, unic. În cursul probei, autorul analizează fiecare caz în detaliu. În primul rând, se ia situația când vectorul dat este zero și, în al doilea rând, când vectorul este diferit de zero. În timpul probei se folosesc ilustrații sub formă de desene și construcții, notații matematice, care formează alfabetizarea matematică în rândul școlarilor. Autorul vorbește încet, ceea ce le permite elevilor să ia note în paralel în timp ce comentează. Construcția efectuată de autor în cursul dovedirii enunțului formulat anterior arată cum se poate construi dintr-un anumit punct un vector egal cu cel dat.

Dacă elevii urmăresc cu atenție lecția și iau note în același timp, vor învăța cu ușurință materialul. Mai mult, autorul povestește în detaliu, măsurat și destul de complet. Dacă dintr-un motiv oarecare nu ați auzit ceva, puteți să vă întoarceți și să vizionați din nou lecția.

După vizionarea tutorialului video, este indicat să începeți repararea materialului. Profesorului i se recomandă să aleagă sarcini pe această temă pentru a-și dezvolta deprinderea de a amâna vectorul dintr-un punct dat.

Această lecție poate fi folosită pentru auto-studiul subiectului de către elevi. Dar pentru a consolida, trebuie să contactați profesorul, astfel încât acesta să selecteze sarcinile adecvate. Într-adevăr, fără consolidarea materialului, este dificil să obții un rezultat pozitiv la antrenament.