Τα μαθηματικά είναι αυτόοι άνθρωποι ελέγχουν τη φύση και τον εαυτό τους.
Ο Σοβιετικός μαθηματικός, ακαδημαϊκός A.N. Κολμογκόροφ
Γεωμετρική πρόοδος.
Μαζί με τις εργασίες για αριθμητικές προόδους, οι εργασίες που σχετίζονται με την έννοια της γεωμετρικής προόδου είναι επίσης κοινές στις εισαγωγικές δοκιμασίες στα μαθηματικά. Για να επιλύσετε με επιτυχία τέτοια προβλήματα, πρέπει να γνωρίζετε τις ιδιότητες μιας γεωμετρικής προόδου και να έχετε καλές δεξιότητες στη χρήση τους.
Αυτό το άρθρο είναι αφιερωμένο στην παρουσίαση των κύριων ιδιοτήτων μιας γεωμετρικής προόδου. Παρέχει επίσης παραδείγματα επίλυσης τυπικών προβλημάτων, δανείστηκε από τις εργασίες των εισαγωγικών τεστ στα μαθηματικά.
Ας σημειώσουμε προκαταρκτικά τις κύριες ιδιότητες μιας γεωμετρικής προόδου και ας θυμηθούμε τους πιο σημαντικούς τύπους και δηλώσεις, συνδέονται με αυτή την έννοια.
Ορισμός.Μια αριθμητική ακολουθία ονομάζεται γεωμετρική πρόοδος εάν κάθε αριθμός της, ξεκινώντας από τον δεύτερο, είναι ίσος με τον προηγούμενο, πολλαπλασιαζόμενος με τον ίδιο αριθμό. Ο αριθμός ονομάζεται παρονομαστής μιας γεωμετρικής προόδου.
Για μια γεωμετρική πρόοδοοι τύποι ισχύουν
, (1)
όπου . Ο τύπος (1) ονομάζεται τύπος του γενικού όρου μιας γεωμετρικής προόδου και ο τύπος (2) είναι η κύρια ιδιότητα μιας γεωμετρικής προόδου: κάθε μέλος της προόδου συμπίπτει με τον γεωμετρικό μέσο όρο των γειτονικών μελών του και .
Σημείωση, ότι ακριβώς λόγω αυτής της ιδιότητας η εν λόγω εξέλιξη ονομάζεται «γεωμετρική».
Οι τύποι (1) και (2) παραπάνω συνοψίζονται ως εξής:
, (3)
Για να υπολογίσετε το άθροισμαπρώτα μέλη μιας γεωμετρικής προόδουισχύει ο τύπος
Αν ορίσουμε
όπου . Επειδή , ο τύπος (6) είναι μια γενίκευση του τύπου (5).
Στην περίπτωση που και γεωμετρική πρόοδοςμειώνεται απείρως. Για να υπολογίσετε το άθροισμαγια όλα τα μέλη μιας απεριόριστα φθίνουσας γεωμετρικής προόδου, χρησιμοποιείται ο τύπος
. (7)
Για παράδειγμα , χρησιμοποιώντας τον τύπο (7), μπορεί κανείς να δείξει, τι
όπου . Αυτές οι ισότητες λαμβάνονται από τον τύπο (7) με την προϋπόθεση ότι , (η πρώτη ισότητα) και , (η δεύτερη ισότητα).
Θεώρημα.Αν τότε
Απόδειξη. Αν τότε ,
Το θεώρημα έχει αποδειχθεί.
Ας προχωρήσουμε στην εξέταση παραδειγμάτων επίλυσης προβλημάτων στο θέμα "Γεωμετρική πρόοδος".
Παράδειγμα 1Δίνονται: , και . Εύρημα .
Λύση.Εάν εφαρμόζεται ο τύπος (5), τότε
Απάντηση: .
Παράδειγμα 2Αφήστε και . Εύρημα .
Λύση.Αφού και , χρησιμοποιούμε τους τύπους (5), (6) και παίρνουμε το σύστημα των εξισώσεων
Αν η δεύτερη εξίσωση του συστήματος (9) διαιρεθεί με την πρώτη, τότε ή . Από αυτό προκύπτει . Ας εξετάσουμε δύο περιπτώσεις.
1. Εάν, τότε από την πρώτη εξίσωση του συστήματος (9) έχουμε.
2. Αν , τότε .
Παράδειγμα 3Αφήστε , και . Εύρημα .
Λύση.Από τον τύπο (2) προκύπτει ότι ή . Από τότε ή .
Κατά συνθήκη. Ωστόσο , επομένως . Επειδή και, τότε εδώ έχουμε ένα σύστημα εξισώσεων
Εάν η δεύτερη εξίσωση του συστήματος διαιρεθεί με την πρώτη, τότε ή .
Επειδή , η εξίσωση έχει μια ενιαία κατάλληλη ρίζα . Στην περίπτωση αυτή, η πρώτη εξίσωση του συστήματος συνεπάγεται .
Λαμβάνοντας υπόψη τον τύπο (7), παίρνουμε.
Απάντηση: .
Παράδειγμα 4Δεδομένα: και . Εύρημα .
Λύση.Από τότε .
Επειδή, τότε ή
Σύμφωνα με τον τύπο (2), έχουμε . Από την άποψη αυτή, από την ισότητα (10) λαμβάνουμε ή .
Ωστόσο, κατά συνθήκη, επομένως.
Παράδειγμα 5Είναι γνωστό ότι . Εύρημα .
Λύση. Σύμφωνα με το θεώρημα, έχουμε δύο ισότητες
Από τότε ή . Γιατί, λοιπόν.
Απάντηση: .
Παράδειγμα 6Δεδομένα: και . Εύρημα .
Λύση.Λαμβάνοντας υπόψη τον τύπο (5), παίρνουμε
Από τότε . Από , και , τότε .
Παράδειγμα 7Αφήστε και . Εύρημα .
Λύση.Σύμφωνα με τον τύπο (1), μπορούμε να γράψουμε
Επομένως, έχουμε ή . Είναι γνωστό ότι και , επομένως και .
Απάντηση: .
Παράδειγμα 8Βρείτε τον παρονομαστή μιας άπειρης φθίνουσας γεωμετρικής προόδου αν
και .
Λύση. Από τον τύπο (7) προκύπτεικαι . Από εδώ και από την συνθήκη του προβλήματος, παίρνουμε το σύστημα των εξισώσεων
Αν η πρώτη εξίσωση του συστήματος είναι τετράγωνο, και μετά διαιρέστε την εξίσωση που προκύπτει με τη δεύτερη εξίσωση, τότε παίρνουμε
Ή .
Απάντηση: .
Παράδειγμα 9Βρείτε όλες τις τιμές για τις οποίες η ακολουθία , , είναι γεωμετρική πρόοδος.
Λύση.Αφήστε , και . Σύμφωνα με τον τύπο (2), που ορίζει την κύρια ιδιότητα μιας γεωμετρικής προόδου, μπορούμε να γράψουμε ή .
Από εδώ παίρνουμε την τετραγωνική εξίσωση, του οποίου οι ρίζες είναικαι .
Ας ελέγξουμε: αν, τότε , και ; αν , τότε , και .
Στην πρώτη περίπτωση έχουμεκαι , και στο δεύτερο - και .
Απάντηση: , .
Παράδειγμα 10λύσει την εξίσωση
, (11)
πού και .
Λύση. Η αριστερή πλευρά της εξίσωσης (11) είναι το άθροισμα μιας άπειρης φθίνουσας γεωμετρικής προόδου, στην οποία και , με την προϋπόθεση: και .
Από τον τύπο (7) προκύπτει, τι . Από αυτή την άποψη, η εξίσωση (11) παίρνει τη μορφήή . κατάλληλη ρίζα τετραγωνική εξίσωση είναι
Απάντηση: .
Παράδειγμα 11.Π ακολουθία θετικών αριθμώνσχηματίζει μια αριθμητική πρόοδο, ένα - γεωμετρική πρόοδος, τι σχέση έχει . Εύρημα .
Λύση.Επειδή αριθμητική ακολουθία, έπειτα (η κύρια ιδιότητα μιας αριθμητικής προόδου). Επειδή η, τότε ή . Αυτό υπονοεί , ότι η γεωμετρική πρόοδος είναι. Σύμφωνα με τον τύπο (2), τότε γράφουμε ότι .
Από και τότε . Στην περίπτωση αυτή, η έκφρασηπαίρνει τη μορφή ή . Κατά συνθήκη, έτσι από την εξίσωσηπαίρνουμε τη μοναδική λύση του προβλήματος που εξετάζουμε, δηλ. .
Απάντηση: .
Παράδειγμα 12.Υπολογίστε το άθροισμα
. (12)
Λύση. Πολλαπλασιάστε και τις δύο πλευρές της ισότητας (12) επί 5 και λάβετε
Αν αφαιρέσουμε το (12) από την παράσταση που προκύπτει, έπειτα
ή .
Για να υπολογίσουμε, αντικαθιστούμε τις τιμές στον τύπο (7) και λαμβάνουμε . Από τότε .
Απάντηση: .
Τα παραδείγματα επίλυσης προβλημάτων που δίνονται εδώ θα είναι χρήσιμα στους υποψηφίους κατά την προετοιμασία για τις εισαγωγικές εξετάσεις. Για μια βαθύτερη μελέτη των μεθόδων επίλυσης προβλημάτων, συνδέεται με μια γεωμετρική πρόοδο, μπορείτε να χρησιμοποιήσετε τα σεμινάρια από τη λίστα της προτεινόμενης βιβλιογραφίας.
1. Συλλογή εργασιών στα μαθηματικά για υποψήφιους ΤΕΙ / Εκδ. ΜΙ. Σκανάβι. – Μ.: Mir i Obrazovanie, 2013. – 608 σελ.
2. Suprun V.P. Μαθηματικά για μαθητές γυμνασίου: πρόσθετες ενότητες του σχολικού προγράμματος. – M.: Lenand / URSS, 2014. - 216 σελ.
3. Medynsky M.M. Ένα πλήρες μάθημα στοιχειωδών μαθηματικών σε εργασίες και ασκήσεις. Βιβλίο 2: Ακολουθίες αριθμών και προόδους. – Μ.: Editus, 2015. - 208 σελ.
Έχετε ερωτήσεις;
Για να λάβετε τη βοήθεια ενός δασκάλου - εγγραφείτε.
site, με πλήρη ή μερική αντιγραφή του υλικού, απαιτείται σύνδεσμος στην πηγή.
Σχετικό μάθημα «Απεριόριστα φθίνουσα γεωμετρική πρόοδος»
Σκοπός του μαθήματος:εισάγοντας τους μαθητές σε ένα νέο είδος ακολουθίας - μια απεριόριστα φθίνουσα γεωμετρική πρόοδο.
Καθήκοντα:
διατύπωση της αρχικής ιδέας του ορίου της αριθμητικής ακολουθίας. γνωριμία με έναν άλλο τρόπο μετατροπής άπειρων περιοδικών κλασμάτων σε συνηθισμένα χρησιμοποιώντας τον τύπο για το άθροισμα μιας απείρως φθίνουσας γεωμετρικής προόδου.
η ανάπτυξη των πνευματικών ιδιοτήτων της προσωπικότητας των μαθητών, όπως η λογική σκέψη, η ικανότητα για αξιολογικές ενέργειες, η γενίκευση.
εκπαίδευση δραστηριότητας, αλληλοβοήθεια, συλλογικότητα, ενδιαφέρον για το αντικείμενο.
Εξοπλισμός:τάξη υπολογιστή, προβολέας, οθόνη.
Τύπος μαθήματος:Μάθημα - κατάκτηση νέου θέματος.
Κατά τη διάρκεια των μαθημάτων
Εγώ . Οργ. στιγμή. Μήνυμα για το θέμα και το σκοπό του μαθήματος.
II . Επικαιροποίηση των γνώσεων των μαθητών.1. Έλεγχος της εργασίας.
1) Επαλήθευση βασικών τύπων που σχετίζονται με αριθμητικές και γεωμετρικές προόδους. Δύο μαθητές σημειώνουν τύπους στον πίνακα.
2) Οι υπόλοιποι μαθητές το κάνουν μαθηματική υπαγόρευση με θέμα «Τύποι αθροίσματος».
Καθήκοντα:
№1. Βρείτε το άθροισμα των πρώτων πέντε μελών μιας αριθμητικής προόδου αν το πρώτο μέλος της είναι 6 (1η επιλογή), -20 (2η επιλογή) και το πέμπτο μέλος είναι -6 (1η επιλογή), 20 (2η επιλογή).
№2. Βρείτε το άθροισμα των πρώτων πέντε όρων μιας αριθμητικής προόδου αν ο πρώτος όρος της είναι -20 (1η επιλογή), 6 (2η επιλογή) και η διαφορά είναι 10 (1η επιλογή), -3 (2η επιλογή).
№3. Βρείτε το άθροισμα των πρώτων πέντε όρων μιας γεωμετρικής προόδου αν ο πρώτος όρος της είναι 1(1η επιλογή), -1 (2η επιλογή) και ο παρονομαστής είναι -2(1η επιλογή), 2(2η επιλογή).
Στο τέλος της υπαγόρευσης, επιλεκτικά, ελέγχονται οι εργασίες δύο μαθητών για αξιολόγηση, οι υπόλοιποι κάνουν αυτοεξέταση σύμφωνα με έτοιμες λύσεις γραμμένες στα πέτα του πίνακα.
Λύσεις:

Καθήκοντα
1. Η αριθμητική πρόοδος δίνεται από τον τύπο ένα n = 7 – 4 n. Εύρημα ένα 10 . (-33)
2. Αριθμητική πρόοδος ένα 3 = 7 και ένα 5 = 1 . Εύρημα ένα 4 . (4)
3. Αριθμητική πρόοδος ένα 3 = 7 και ένα 5 = 1 . Εύρημα ένα 17 . (-35)
4. Αριθμητική πρόοδος ένα 3 = 7 και ένα 5 = 1 . Εύρημα μικρό 17 . (-187)
5. Για μια γεωμετρική πρόοδο  βρείτε τον πέμπτο όρο.
βρείτε τον πέμπτο όρο. 
6. Για μια γεωμετρική πρόοδο  εύρημα n-ο μέλος.
εύρημα n-ο μέλος. 
7. Εκθετικά σι 3 = 8 και σι 5 = 2 . Εύρημα σι 4 . (4)
8. Εκθετικά σι
3
= 8
και σι
5
= 2
. Εύρημα σι
1
και
q
. 
9. Εκθετικά σι 3 = 8 και σι 5 = 2 . Εύρημα μικρό 5 . (62)
III . Εξερευνώντας ένα νέο θέμα(παρουσίαση επίδειξης).

Θεωρούμε ένα τετράγωνο με πλευρά ίση με 1. Ας σχεδιάσουμε ένα άλλο τετράγωνο, η πλευρά του οποίου είναι το μισό του πρώτου τετραγώνου, μετά ένα άλλο, η πλευρά του οποίου είναι το μισό του δεύτερου, μετά το επόμενο κ.ο.κ. Κάθε φορά η πλευρά του νέου τετραγώνου είναι η μισή από την προηγούμενη.
Ως αποτέλεσμα, πήραμε μια ακολουθία πλευρών τετραγώνων  σχηματίζοντας μια γεωμετρική πρόοδο με παρονομαστή .
σχηματίζοντας μια γεωμετρική πρόοδο με παρονομαστή .
Και, αυτό που είναι πολύ σημαντικό, όσο περισσότερο χτίζουμε τέτοια τετράγωνα, τόσο μικρότερη θα είναι η πλευρά του τετραγώνου. Για παράδειγμα,

Εκείνοι. καθώς ο αριθμός n αυξάνεται, οι όροι της προόδου πλησιάζουν το μηδέν.
Με τη βοήθεια αυτού του σχήματος, μπορεί να εξεταστεί μια ακόμη ακολουθία.

Για παράδειγμα, η ακολουθία εμβαδών τετραγώνων:

 . Και, πάλι, αν nαυξάνεται επ 'αόριστον, τότε η περιοχή πλησιάζει το μηδέν αυθαίρετα κλείσιμο.
. Και, πάλι, αν nαυξάνεται επ 'αόριστον, τότε η περιοχή πλησιάζει το μηδέν αυθαίρετα κλείσιμο.
Ας εξετάσουμε ένα ακόμη παράδειγμα. Ισόπλευρο τρίγωνο με πλευρά 1 cm. Ας χτίσουμε το επόμενο τρίγωνο με κορυφές στα μέσα των πλευρών του 1ου τριγώνου, σύμφωνα με το θεώρημα της μέσης γραμμής του τριγώνου - η πλευρά του 2ου είναι ίση με τη μισή πλευρά του πρώτου, η πλευρά του 3ου είναι η μισή πλευρά του το 2ο κ.λπ. Και πάλι παίρνουμε μια ακολουθία μηκών των πλευρών των τριγώνων.
 στο
στο  .
.
Αν θεωρήσουμε μια γεωμετρική πρόοδο με αρνητικό παρονομαστή.
Μετά, πάλι, με αυξανόμενους αριθμούς nοι όροι της προσέγγισης προόδου μηδέν.
Ας προσέξουμε τους παρονομαστές αυτών των ακολουθιών. Παντού οι παρονομαστές ήταν λιγότεροι από 1 modulo.
Μπορούμε να συμπεράνουμε: μια γεωμετρική πρόοδος θα είναι απείρως φθίνουσα αν το μέτρο του παρονομαστή της είναι μικρότερο από 1.
Μπροστινή εργασία.
Ορισμός:
Μια γεωμετρική πρόοδος λέγεται ότι μειώνεται άπειρα αν το μέτρο του παρονομαστή της είναι μικρότερο από ένα.  .
.
Με τη βοήθεια του ορισμού, είναι δυνατό να λυθεί το ερώτημα εάν μια γεωμετρική πρόοδος μειώνεται απεριόριστα ή όχι.
Μια εργασία
Είναι η ακολουθία μια απείρως φθίνουσα γεωμετρική πρόοδος αν δίνεται από τον τύπο:
 ;
;  .
.
Λύση:
 . Ας βρούμε q
.
. Ας βρούμε q
.
 ;
;  ;
;  ;
;  .
.
αυτή η γεωμετρική πρόοδος μειώνεται απείρως.
σι)αυτή η ακολουθία δεν είναι μια απεριόριστα φθίνουσα γεωμετρική πρόοδος.

Θεωρήστε ένα τετράγωνο με πλευρά ίση με 1. Χωρίστε το στη μέση, ένα από τα μισά πάλι στη μέση κ.ο.κ. τα εμβαδά όλων των παραλληλόγραμμων που προκύπτουν σχηματίζουν μια απεριόριστα φθίνουσα γεωμετρική πρόοδο: ![]()
Το άθροισμα των εμβαδών όλων των ορθογωνίων που λαμβάνονται με αυτόν τον τρόπο θα είναι ίσο με το εμβαδόν του 1ου τετραγώνου και ίσο με 1. ![]()
Αλλά στην αριστερή πλευρά αυτής της ισότητας βρίσκεται το άθροισμα ενός άπειρου αριθμού όρων.
Θεωρήστε το άθροισμα των πρώτων n όρων. ![]()
Σύμφωνα με τον τύπο για το άθροισμα των πρώτων n όρων μιας γεωμετρικής προόδου, ισούται με  .
.
Αν ένα nαυξάνεται επ' αόριστον, λοιπόν
ή  . Να γιατί
. Να γιατί  , δηλ.
, δηλ.  .
.
Το άθροισμα μιας απείρως φθίνουσας γεωμετρικής προόδουυπάρχει όριο ακολουθίας μικρό 1 , μικρό 2 , μικρό 3 , …, μικρό n , … .
Για παράδειγμα, για μια εξέλιξη  ,
,
 Επειδή
Επειδή 
Το άθροισμα μιας απείρως φθίνουσας γεωμετρικής προόδουμπορεί να βρεθεί χρησιμοποιώντας τον τύπο 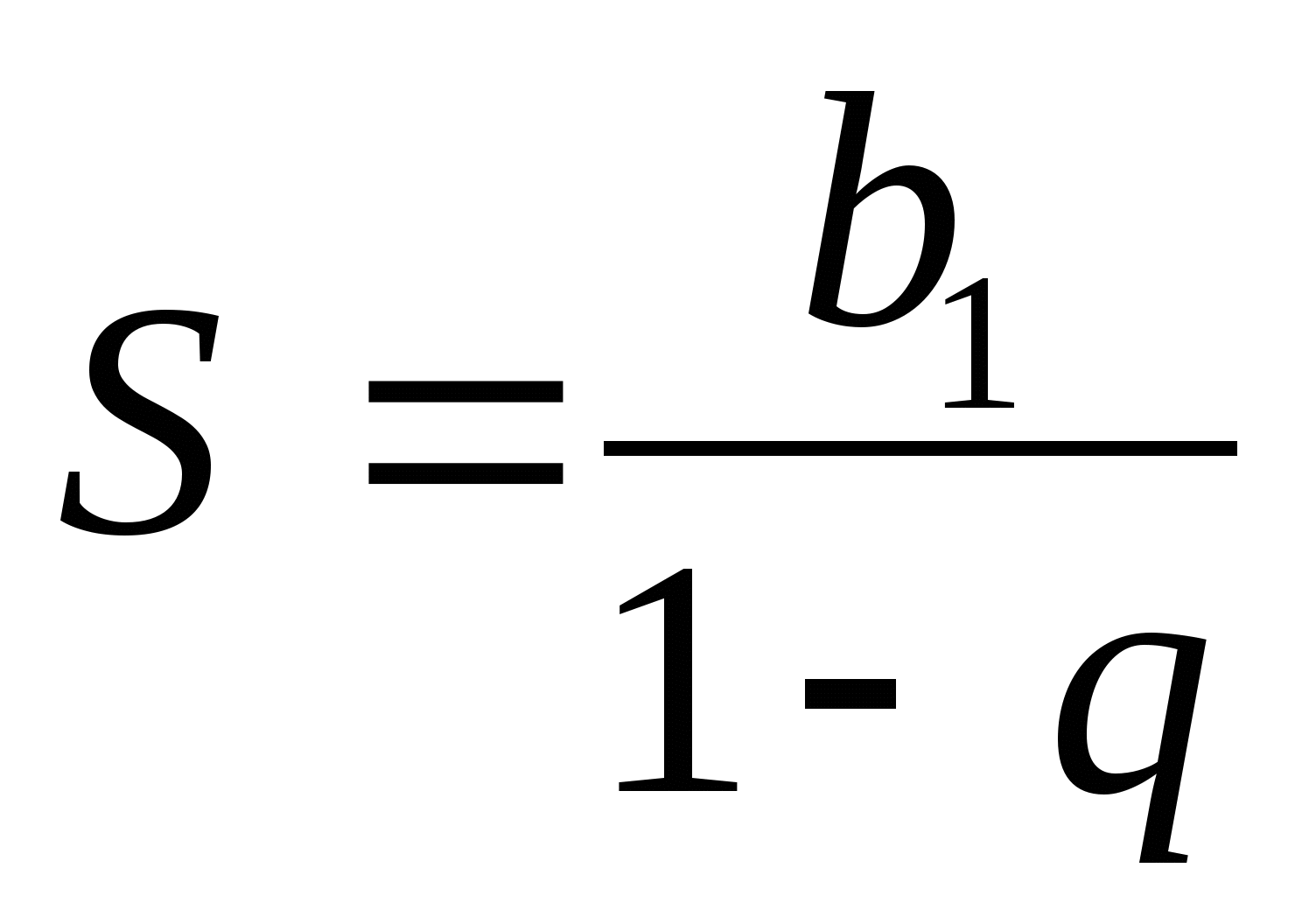 .
.
III . Προβληματισμός και εμπέδωση(ολοκλήρωση εργασιών).
Εργασία αριθμός 2. Βρείτε το άθροισμα μιας απεριόριστα φθίνουσας γεωμετρικής προόδου με τον πρώτο όρο 3, τον δεύτερο 0,3.
Λύση:
Εργασία αριθμός 3. σχολικό βιβλίο, σελ. 160, Αρ. 433(1)
Βρείτε το άθροισμα μιας απεριόριστα φθίνουσας γεωμετρικής προόδου:
Λύση:

Εργασία αριθμός 4. Γράψτε το άπειρο περιοδικό δεκαδικό κλάσμα 0,(5) ως κοινό κλάσμα.
1ος τρόπος. Έστω x = 0, (5) = 0,555 ... / 10 2η μέθοδος. 0,(5)=0,555…=

Εργασία αριθμός 5. σχολικό βιβλίο, σελ. 162, Αρ. 445(3) (αυτοτελής απόφαση)
Γράψτε το άπειρο περιοδικό δεκαδικό κλάσμα 0,(12) ως κοινό κλάσμα.
Απάντηση: 0,(12)=4/33.
IV . Συνοψίζοντας.
Τι ακολουθία συναντήσατε σήμερα;
Ορίστε μια απεριόριστα φθίνουσα γεωμετρική πρόοδο.
Πώς να αποδείξετε ότι μια γεωμετρική πρόοδος μειώνεται απείρως;
Δώστε τον τύπο για το άθροισμα μιας απεριόριστα φθίνουσας γεωμετρικής προόδου.
V . Εργασία για το σπίτι.
Μάθημα και παρουσίαση με θέμα: "Ακολουθίες αριθμών. Γεωμετρική πρόοδος"
Πρόσθετα υλικά
Αγαπητοί χρήστες, μην ξεχάσετε να αφήσετε τα σχόλια, τα σχόλια, τις προτάσεις σας! Όλα τα υλικά ελέγχονται από ένα πρόγραμμα προστασίας από ιούς.
Διδακτικά βοηθήματα και προσομοιωτές στο ηλεκτρονικό κατάστημα "Integral" για την 9η τάξη
Powers and Roots Συναρτήσεις και γραφήματα
Παιδιά, σήμερα θα γνωρίσουμε ένα άλλο είδος εξέλιξης.
Το θέμα του σημερινού μαθήματος είναι η γεωμετρική πρόοδος.
Γεωμετρική πρόοδος
Ορισμός. Μια αριθμητική ακολουθία στην οποία κάθε όρος, ξεκινώντας από τον δεύτερο, ισούται με το γινόμενο του προηγούμενου και κάποιου σταθερού αριθμού, ονομάζεται γεωμετρική πρόοδος.Ας ορίσουμε την ακολουθία μας αναδρομικά: $b_(1)=b$, $b_(n)=b_(n-1)*q$,
όπου b και q είναι ορισμένοι δεδομένοι αριθμοί. Ο αριθμός q ονομάζεται παρονομαστής της προόδου.
Παράδειγμα. 1,2,4,8,16… Γεωμετρική πρόοδος, στην οποία το πρώτο μέλος είναι ίσο με ένα και $q=2$.
Παράδειγμα. 8,8,8,8… Μια γεωμετρική πρόοδος της οποίας ο πρώτος όρος είναι οκτώ,
και $q=1$.
Παράδειγμα. 3,-3,3,-3,3... Μια γεωμετρική πρόοδος της οποίας ο πρώτος όρος είναι τρεις,
και $q=-1$.
Η γεωμετρική πρόοδος έχει τις ιδιότητες της μονοτονίας.
Αν $b_(1)>0$, $q>1$,
τότε η σειρά αυξάνεται.
Αν $b_(1)>0$, $0 Η ακολουθία συνήθως συμβολίζεται ως: $b_(1), b_(2), b_(3), ..., b_(n), ...$.
Ακριβώς όπως σε μια αριθμητική πρόοδο, εάν ο αριθμός των στοιχείων σε μια γεωμετρική πρόοδο είναι πεπερασμένος, τότε η πρόοδος ονομάζεται πεπερασμένη γεωμετρική πρόοδος.
$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$.
Σημειώστε ότι εάν η ακολουθία είναι μια γεωμετρική πρόοδος, τότε η ακολουθία των τετραγωνικών όρων είναι επίσης μια γεωμετρική πρόοδος. Η δεύτερη ακολουθία έχει τον πρώτο όρο $b_(1)^2$ και τον παρονομαστή $q^2$.
Τύπος του ν' μέλους μιας γεωμετρικής προόδου
Η γεωμετρική πρόοδος μπορεί επίσης να προσδιοριστεί σε αναλυτική μορφή. Ας δούμε πώς να το κάνουμε:$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$.
$b_(4)=b_(3)*q=b_(1)*q^3$.
$b_(5)=b_(4)*q=b_(1)*q^4$.
Μπορούμε εύκολα να δούμε το μοτίβο: $b_(n)=b_(1)*q^(n-1)$.
Ο τύπος μας ονομάζεται "τύπος του ν-ου μέλους μιας γεωμετρικής προόδου".
Ας επιστρέψουμε στα παραδείγματά μας.
Παράδειγμα. 1,2,4,8,16… Μια γεωμετρική πρόοδος της οποίας ο πρώτος όρος είναι ίσος με ένα,
και $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$.
Παράδειγμα. 16,8,4,2,1,1/2… Μια γεωμετρική πρόοδος της οποίας ο πρώτος όρος είναι δεκαέξι και $q=\frac(1)(2)$.
$b_(n)=16*(\frac(1)(2))^(n-1)$.
Παράδειγμα. 8,8,8,8… Μια γεωμετρική πρόοδος όπου ο πρώτος όρος είναι οκτώ και $q=1$.
$b_(n)=8*1^(n-1)=8$.
Παράδειγμα. 3,-3,3,-3,3… Μια γεωμετρική πρόοδος της οποίας ο πρώτος όρος είναι τρεις και $q=-1$.
$b_(n)=3*(-1)^(n-1)$.
Παράδειγμα. Δίνεται μια γεωμετρική πρόοδος $b_(1), b_(2), …, b_(n), … $.
α) Είναι γνωστό ότι $b_(1)=6, q=3$. Βρείτε $b_(5)$.
β) Είναι γνωστό ότι $b_(1)=6, q=2, b_(n)=768$. Εύρεση n.
γ) Είναι γνωστό ότι $q=-2, b_(6)=96$. Βρείτε $b_(1)$.
δ) Είναι γνωστό ότι $b_(1)=-2, b_(12)=4096$. Βρείτε q.
Λύση.
α) $b_(5)=b_(1)*q^4=6*3^4=486$.
β) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$.
$2^(n-1)=\frac(768)(6)=128$ αφού $2^7=128 => n-1=7; n=8$.
γ) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$.
δ) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.
Παράδειγμα. Η διαφορά μεταξύ του έβδομου και του πέμπτου μέλους της γεωμετρικής προόδου είναι 192, το άθροισμα του πέμπτου και του έκτου μέλους της προόδου είναι 192. Βρείτε το δέκατο μέλος αυτής της προόδου.
Λύση.
Γνωρίζουμε ότι: $b_(7)-b_(5)=192$ και $b_(5)+b_(6)=192$.
Γνωρίζουμε επίσης: $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Επειτα:
$b_(1)*q^6-b_(1)*q^4=192$.
$b_(1)*q^4+b_(1)*q^5=192$.
Έχουμε ένα σύστημα εξισώσεων:
$\begin(περιπτώσεις)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\end(περιπτώσεις)$.
Εξισώνοντας, οι εξισώσεις μας παίρνουν:
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
Πήραμε δύο λύσεις q: $q_(1)=2, q_(2)=-1$.
Αντικαταστήστε διαδοχικά στη δεύτερη εξίσωση:
$b_(1)*2^4*3=192 => b_(1)=4$.
$b_(1)*(-1)^4*0=192 =>$ δεν υπάρχουν λύσεις.
Πήραμε ότι: $b_(1)=4, q=2$.
Ας βρούμε τον δέκατο όρο: $b_(10)=b_(1)*q^9=4*2^9=2048$.
Το άθροισμα μιας πεπερασμένης γεωμετρικής προόδου
Ας υποθέσουμε ότι έχουμε μια πεπερασμένη γεωμετρική πρόοδο. Ας υπολογίσουμε, όπως και για μια αριθμητική πρόοδο, το άθροισμα των μελών της.Έστω μια πεπερασμένη γεωμετρική πρόοδος: $b_(1),b_(2),…,b_(n-1),b_(n)$.
Ας εισάγουμε τον συμβολισμό για το άθροισμα των μελών του: $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$.
Στην περίπτωση που $q=1$. Όλα τα μέλη της γεωμετρικής προόδου είναι ίσα με το πρώτο μέλος, τότε είναι προφανές ότι $S_(n)=n*b_(1)$.
Εξετάστε τώρα την περίπτωση $q≠1$.
Πολλαπλασιάστε το παραπάνω ποσό με q.
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$.
Σημείωση:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$.
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$.
$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2 )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$.
$S_(n)(q-1)=b_(n)*q-b_(1)$.
$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.
$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$.
Λάβαμε τον τύπο για το άθροισμα μιας πεπερασμένης γεωμετρικής προόδου.
Παράδειγμα.
Να βρείτε το άθροισμα των επτά πρώτων όρων μιας γεωμετρικής προόδου της οποίας ο πρώτος όρος είναι 4 και ο παρονομαστής είναι 3.
Λύση.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$.
Παράδειγμα.
Βρείτε το πέμπτο μέλος της γεωμετρικής προόδου, το οποίο είναι γνωστό: $b_(1)=-3$; $b_(n)=-3072$; $S_(n)=-4095$.
Λύση.
$b_(n)=(-3)*q^(n-1)=-3072$.
$q^(n-1)=1024$.
$q^(n)=1024q$.
$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$.
$-4095(q-1)=-3*(q^(n)-1)$.
-4095$(q-1)=-3*(1024q-1)$.
$1365q-1365=1024q-1$.
$341q=1364$.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$.
Χαρακτηριστική ιδιότητα μιας γεωμετρικής προόδου
Παιδιά, δίνεται μια γεωμετρική πρόοδος. Ας εξετάσουμε τα τρία διαδοχικά μέλη του: $b_(n-1),b_(n),b_(n+1)$.Ξέρουμε ότι:
$\frac(b_(n))(q)=b_(n-1)$.
$b_(n)*q=b_(n+1)$.
Επειτα:
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$.
Εάν η πρόοδος είναι πεπερασμένη, τότε αυτή η ισότητα ισχύει για όλους τους όρους εκτός από τον πρώτο και τον τελευταίο.
Εάν δεν είναι γνωστό εκ των προτέρων τι είδους ακολουθία έχει η ακολουθία, αλλά είναι γνωστό ότι: $b_(n)^(2)=b_(n-1)*b_(n+1)$.
Τότε μπορούμε να πούμε με ασφάλεια ότι πρόκειται για μια γεωμετρική πρόοδο.
Μια αριθμητική ακολουθία είναι μια γεωμετρική πρόοδος μόνο όταν το τετράγωνο καθενός από τους όρους της είναι ίσο με το γινόμενο των δύο γειτονικών της όρων της προόδου. Μην ξεχνάτε ότι για μια πεπερασμένη εξέλιξη αυτή η συνθήκη δεν ικανοποιείται για τον πρώτο και τον τελευταίο όρο.
Ας δούμε αυτήν την ταυτότητα: $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$.
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
Το $\sqrt(a*b)$ ονομάζεται γεωμετρικός μέσος όρος των a και b.
Ο συντελεστής συντελεστή οποιουδήποτε μέλους μιας γεωμετρικής προόδου είναι ίσος με τον γεωμετρικό μέσο όρο των δύο μελών που βρίσκονται δίπλα του.
Παράδειγμα.
Βρείτε το x τέτοιο ώστε $x+2; 2x+2; 3x+3$ ήταν τρία διαδοχικά μέλη μιας γεωμετρικής προόδου.
Λύση.
Ας χρησιμοποιήσουμε την χαρακτηριστική ιδιότητα:
$(2x+2)^2=(x+2)(3x+3)$.
$4x^2+8x+4=3x^2+3x+6x+6$.
$x^2-x-2=0$.
$x_(1)=2$ και $x_(2)=-1$.
Αντικαταστήστε διαδοχικά στην αρχική έκφραση, τις λύσεις μας:
Με $x=2$, πήραμε την ακολουθία: 4;6;9 είναι μια γεωμετρική πρόοδος με $q=1,5$.
Με $x=-1$, πήραμε την ακολουθία: 1;0;0.
Απάντηση: $x=2,$
Εργασίες για ανεξάρτητη λύση
1. Βρείτε το όγδοο πρώτο μέλος της γεωμετρικής προόδου 16, -8, 4, -2 ....2. Βρείτε το δέκατο μέλος της γεωμετρικής προόδου 11,22,44….
3. Είναι γνωστό ότι $b_(1)=5, q=3$. Βρείτε $b_(7)$.
4. Είναι γνωστό ότι $b_(1)=8, q=-2, b_(n)=512$. Εύρεση n.
5. Βρείτε το άθροισμα των πρώτων 11 μελών της γεωμετρικής προόδου 3;12;48….
6. Βρείτε το x έτσι ώστε $3x+4; 2x+4; Τα x+5$ είναι τρία διαδοχικά μέλη μιας γεωμετρικής προόδου.
ΑΡΙΘΜΗΤΙΚΕΣ ΑΚΟΛΟΥΘΙΕΣ VI
§ 148. Το άθροισμα μιας απείρως φθίνουσας γεωμετρικής προόδου
Μέχρι τώρα, μιλώντας για αθροίσματα, πάντα υποθέταμε ότι ο αριθμός των όρων σε αυτά τα αθροίσματα είναι πεπερασμένος (για παράδειγμα, 2, 15, 1000 κ.λπ.). Αλλά όταν λύνουμε ορισμένα προβλήματα (ειδικά ανώτερα μαθηματικά), πρέπει να ασχοληθούμε με τα αθροίσματα ενός άπειρου αριθμού όρων
S= ένα 1 + ένα 2 + ... + ένα n + ... . (1)
Ποια είναι αυτά τα ποσά; Εξ ορισμού το άθροισμα ενός άπειρου αριθμού όρων ένα 1 , ένα 2 , ..., ένα n , ... ονομάζεται όριο του αθροίσματος S n πρώτα Π αριθμοί όταν Π -> ∞ :
S=S n = (ένα 1 + ένα 2 + ... + ένα n ). (2)
Το όριο (2), φυσικά, μπορεί να υπάρχει ή να μην υπάρχει. Κατά συνέπεια, το άθροισμα (1) λέγεται ότι υπάρχει ή δεν υπάρχει.
Πώς να μάθετε εάν το άθροισμα (1) υπάρχει σε κάθε συγκεκριμένη περίπτωση; Μια γενική λύση σε αυτό το ερώτημα υπερβαίνει κατά πολύ το πεδίο του προγράμματός μας. Ωστόσο, υπάρχει μια σημαντική ειδική περίπτωση που πρέπει να εξετάσουμε τώρα. Θα μιλήσουμε για το άθροισμα των όρων μιας απείρως φθίνουσας γεωμετρικής προόδου.
Αφήνω ένα 1 , ένα 1 q , ένα 1 q 2 , ... είναι μια απεριόριστα φθίνουσα γεωμετρική πρόοδος. Αυτό σημαίνει ότι | q |< 1. Сумма первых Π μέλη αυτής της προόδου ισούται με
![]()
Από τα βασικά θεωρήματα για τα όρια των μεταβλητών (βλ. § 136) προκύπτει:

Αλλά 1 = 1, α q n = 0. Επομένως

Άρα, το άθροισμα μιας απείρως φθίνουσας γεωμετρικής προόδου είναι ίσο με τον πρώτο όρο αυτής της προόδου διαιρεμένο με το ένα μείον τον παρονομαστή αυτής της προόδου.
1) Το άθροισμα της γεωμετρικής προόδου 1, 1/3, 1/9, 1/27, ... είναι

και το άθροισμα μιας γεωμετρικής προόδου είναι 12. -6; 3; - 3 / 2 , ... ισούται

2) Ένα απλό περιοδικό κλάσμα 0,454545 ... μετατρέπεται σε συνηθισμένο.
Για να λύσουμε αυτό το πρόβλημα, αντιπροσωπεύουμε αυτό το κλάσμα ως άπειρο άθροισμα:
Η δεξιά πλευρά αυτής της ισότητας είναι το άθροισμα μιας απείρως φθίνουσας γεωμετρικής προόδου, ο πρώτος όρος της οποίας είναι 45/100 και ο παρονομαστής είναι 1/100. Να γιατί

Με τον τρόπο που περιγράφηκε, μπορεί επίσης να ληφθεί ο γενικός κανόνας για τη μετατροπή απλών περιοδικών κλασμάτων σε συνηθισμένα κλάσματα (βλ. Κεφάλαιο II, § 38):
Για να μετατρέψετε ένα απλό περιοδικό κλάσμα σε συνηθισμένο, πρέπει να προχωρήσετε ως εξής: βάλτε την περίοδο του δεκαδικού κλάσματος στον αριθμητή και στον παρονομαστή - έναν αριθμό που αποτελείται από εννέα που λαμβάνονται όσες φορές υπάρχουν ψηφία στην περίοδο του δεκαδικού κλάσματος.
3) Μικτό περιοδικό κλάσμα 0,58333 .... μετατρέπεται σε συνηθισμένο κλάσμα.
Ας αντιπροσωπεύσουμε αυτό το κλάσμα ως άπειρο άθροισμα:
Στη δεξιά πλευρά αυτής της ισότητας, όλοι οι όροι, ξεκινώντας από το 3/1000, σχηματίζουν μια απεριόριστα φθίνουσα γεωμετρική πρόοδο, ο πρώτος όρος της οποίας είναι 3/1000 και ο παρονομαστής είναι 1/10. Να γιατί

Με τον τρόπο που περιγράφηκε, μπορεί επίσης να ληφθεί ο γενικός κανόνας για τη μετατροπή μικτών περιοδικών κλασμάτων σε συνηθισμένα κλάσματα (βλ. Κεφάλαιο II, § 38). Δεν το συμπεριλαμβάνουμε εσκεμμένα εδώ. Δεν χρειάζεται να απομνημονεύσετε αυτόν τον δυσκίνητο κανόνα. Είναι πολύ πιο χρήσιμο να γνωρίζουμε ότι οποιοδήποτε μικτό περιοδικό κλάσμα μπορεί να αναπαρασταθεί ως το άθροισμα μιας άπειρα φθίνουσας γεωμετρικής προόδου και κάποιου αριθμού. Και η φόρμουλα
για το άθροισμα μιας απείρως φθίνουσας γεωμετρικής προόδου, πρέπει φυσικά να θυμόμαστε.
Ως άσκηση, σας καλούμε, εκτός από τα προβλήματα Νο. 995-1000 παρακάτω, να στραφείτε και πάλι στο πρόβλημα Νο. 301 § 38.
Γυμνάσια
995. Τι ονομάζεται το άθροισμα μιας απείρως φθίνουσας γεωμετρικής προόδου;
996. Βρείτε αθροίσματα άπειρα φθίνουσας γεωμετρικής προόδου:

997. Για ποιες αξίες Χ προχώρηση
![]()
μειώνεται απείρως; Βρείτε το άθροισμα μιας τέτοιας προόδου.
998. Σε ισόπλευρο τρίγωνο με πλευρά ένα ένα νέο τρίγωνο εγγράφεται συνδέοντας τα μέσα των πλευρών του. ένα νέο τρίγωνο εγγράφεται σε αυτό το τρίγωνο με τον ίδιο τρόπο, και ούτω καθεξής ad infinitum.
α) το άθροισμα των περιμέτρων όλων αυτών των τριγώνων.
β) το άθροισμα των εκτάσεών τους.
999. Σε τετράγωνο με πλευρά ένα ένα νέο τετράγωνο εγγράφεται συνδέοντας τα μεσαία σημεία των πλευρών του. ένα τετράγωνο εγγράφεται σε αυτό το τετράγωνο με τον ίδιο τρόπο, και ούτω καθεξής ad infinitum. Να βρείτε το άθροισμα των περιμέτρων όλων αυτών των τετραγώνων και το άθροισμα των εμβαδών τους.
1000. Κάντε μια απεριόριστα φθίνουσα γεωμετρική πρόοδο, έτσι ώστε το άθροισμά της να είναι ίσο με 25 / 4 και το άθροισμα των τετραγώνων των όρων της να είναι ίσο με 625 / 24.
Μια γεωμετρική πρόοδος είναι ένα νέο είδος αριθμητικής ακολουθίας με το οποίο πρέπει να εξοικειωθούμε. Για μια επιτυχημένη γνωριμία, δεν βλάπτει τουλάχιστον να ξέρεις και να καταλάβεις. Τότε δεν θα υπάρχει πρόβλημα με τη γεωμετρική πρόοδο.)
Τι είναι μια γεωμετρική πρόοδος; Η έννοια της γεωμετρικής προόδου.
Ξεκινάμε την ξενάγηση, ως συνήθως, με τα δημοτικά. Γράφω μια ημιτελή ακολουθία αριθμών:
1, 10, 100, 1000, 10000, …
Μπορείτε να πιάσετε ένα μοτίβο και να πείτε ποιοι αριθμοί θα ακολουθήσουν; Το πιπέρι είναι ξεκάθαρο, οι αριθμοί 100000, 1000000 και ούτω καθεξής θα πάνε παρακάτω. Ακόμα και χωρίς πολύ ψυχικό στρες, όλα είναι ξεκάθαρα, σωστά;)
ΕΝΤΑΞΕΙ. Ενα άλλο παράδειγμα. Γράφω την εξής σειρά:
1, 2, 4, 8, 16, …
Μπορείτε να πείτε ποιοι αριθμοί θα ακολουθήσουν, ακολουθώντας τον αριθμό 16 και το όνομα όγδοομέλος της ακολουθίας; Αν καταλάβατε ότι θα ήταν ο αριθμός 128, τότε πολύ καλά. Άρα, η μισή μάχη είναι στην κατανόηση έννοιακαι βασικά σημείαέχει ήδη γίνει γεωμετρική πρόοδος. Μπορείτε να αναπτυχθείτε περαιτέρω.)
Και τώρα γυρίζουμε ξανά από τις αισθήσεις στα αυστηρά μαθηματικά.
Βασικές στιγμές μιας γεωμετρικής προόδου.
Βασική στιγμή #1
Η γεωμετρική πρόοδος είναι ακολουθία αριθμών.Όπως και η εξέλιξη. Τίποτα δύσκολο. Μόλις κανόνισα αυτή τη σειρά διαφορετικά.Ως εκ τούτου, φυσικά, έχει άλλο όνομα, ναι ...
Βασική στιγμή #2
Με το δεύτερο βασικό σημείο, η ερώτηση θα είναι πιο δύσκολη. Ας πάμε λίγο πίσω και ας θυμηθούμε τη βασική ιδιότητα μιας αριθμητικής προόδου. Εδώ είναι: κάθε μέλος είναι διαφορετικό από το προηγούμενο κατά το ίδιο ποσό.
Είναι δυνατόν να διατυπωθεί μια παρόμοια ιδιότητα κλειδιού για μια γεωμετρική πρόοδο; Σκεφτείτε λίγο... Ρίξτε μια ματιά στα παραδείγματα που δίνονται. Μαντέψατε; Ναί! Σε μια γεωμετρική πρόοδο (οποιαδήποτε!) κάθε μέλος του διαφέρει από το προηγούμενο στις ίδιες φορές.Είναι πάντα!
Στο πρώτο παράδειγμα, αυτός ο αριθμός είναι δέκα. Όποιον όρο της ακολουθίας και αν πάρετε, είναι μεγαλύτερος από τον προηγούμενο δεκα φορες.
Στο δεύτερο παράδειγμα, αυτό είναι δύο: κάθε μέλος είναι μεγαλύτερο από το προηγούμενο. εις διπλούν.
Σε αυτό το βασικό σημείο η γεωμετρική πρόοδος διαφέρει από την αριθμητική. Σε μια αριθμητική πρόοδο, προκύπτει κάθε επόμενος όρος προσθέτωνταςίδιας αξίας με τον προηγούμενο όρο. Και εδώ - πολλαπλασιασμόςτην προηγούμενη περίοδο κατά το ίδιο ποσό. Αυτή είναι η διαφορά.)
Βασική στιγμή #3
Αυτό το βασικό σημείο είναι εντελώς πανομοιότυπο με αυτό για μια αριθμητική πρόοδο. Και συγκεκριμένα: κάθε μέλος της γεωμετρικής προόδου βρίσκεται στη θέση του.Όλα είναι ακριβώς όπως στην αριθμητική πρόοδο και τα σχόλια, νομίζω, είναι περιττά. Υπάρχει ο πρώτος όρος, υπάρχει εκατόν πρώτος και ούτω καθεξής. Ας αναδιατάξουμε τουλάχιστον δύο μέλη - το σχέδιο (και μαζί του η γεωμετρική πρόοδος) θα εξαφανιστεί. Αυτό που μένει είναι απλώς μια ακολουθία αριθμών χωρίς καμία λογική.
Αυτό είναι όλο. Αυτό είναι όλο το νόημα της γεωμετρικής προόδου.
Όροι και ονομασίες.
Και τώρα, έχοντας ασχοληθεί με το νόημα και τα βασικά σημεία της γεωμετρικής προόδου, μπορούμε να προχωρήσουμε στη θεωρία. Διαφορετικά, τι είναι μια θεωρία χωρίς να καταλαβαίνουμε το νόημα, σωστά;
Τι είναι μια γεωμετρική πρόοδος;
Πώς γράφεται με γενικούς όρους μια γεωμετρική πρόοδος; Κανένα πρόβλημα! Κάθε μέλος της προόδου γράφεται επίσης ως γράμμα. Μόνο για αριθμητική πρόοδο, χρησιμοποιείται συνήθως το γράμμα "ένα", για γεωμετρικό - γράμμα "σι". Αριθμός μέλους, ως συνήθως, υποδεικνύεται κάτω δεξιά δείκτης. Τα ίδια τα μέλη της προόδου απλώς παρατίθενται χωρισμένα με κόμμα ή ερωτηματικά.
Σαν αυτό:
β1,σι 2 , σι 3 , σι 4 , σι 5 , σι 6 , …
Εν συντομία, μια τέτοια εξέλιξη γράφεται ως εξής: (b n) .
Ή όπως αυτό, για πεπερασμένες προόδους:
b 1 , b 2 , b 3 , b 4 , b 5 , b 6 .
b 1 , b 2 , ..., b 29 , b 30 .
Ή εν συντομία:
(b n), n=30 .
Αυτό, στην πραγματικότητα, είναι όλοι οι χαρακτηρισμοί. Όλα είναι ίδια, μόνο το γράμμα είναι διαφορετικό, ναι.) Και τώρα πάμε απευθείας στον ορισμό.
Ορισμός γεωμετρικής προόδου.
Μια γεωμετρική πρόοδος είναι μια αριθμητική ακολουθία, της οποίας ο πρώτος όρος είναι μη μηδενικός, και κάθε επόμενος όρος είναι ίσος με τον προηγούμενο όρο πολλαπλασιασμένο με τον ίδιο μη μηδενικό αριθμό.
Αυτός είναι όλος ο ορισμός. Οι περισσότερες λέξεις και φράσεις είναι σαφείς και οικείες σε εσάς. Εκτός βέβαια αν καταλαβαίνεις την έννοια μιας γεωμετρικής προόδου «στα δάχτυλα» και γενικά. Υπάρχουν όμως και μερικές νέες φράσεις στις οποίες θα ήθελα να επιστήσω ιδιαίτερη προσοχή.
Πρώτα, οι λέξεις: «η πρώτη θητεία της οποίας διαφορετικό από το μηδέν".
Αυτός ο περιορισμός στην πρώτη θητεία δεν εισήχθη τυχαία. Τι πιστεύετε ότι θα συμβεί εάν η πρώτη θητεία σι 1 αποδεικνύεται μηδέν; Ποιος θα είναι ο δεύτερος όρος εάν κάθε όρος είναι μεγαλύτερος από τον προηγούμενο τις ίδιες φορές;Ας πούμε τρεις φορές; Ας δούμε... Πολλαπλασιάστε τον πρώτο όρο (δηλαδή 0) με 3 και πάρτε... μηδέν! Και το τρίτο μέλος; Μηδέν επίσης! Και ο τέταρτος όρος είναι επίσης μηδέν! Και ούτω καθεξής…
Παίρνουμε μόνο ένα σακουλάκι με κουλούρια μια ακολουθία μηδενικών:
0, 0, 0, 0, …
Φυσικά, μια τέτοια ακολουθία έχει δικαίωμα στη ζωή, αλλά δεν έχει κανένα πρακτικό ενδιαφέρον. Όλα είναι τόσο ξεκάθαρα. Οποιοδήποτε από τα μέλη του είναι μηδέν. Το άθροισμα οποιουδήποτε αριθμού μελών είναι επίσης μηδέν ... Τι ενδιαφέροντα πράγματα μπορείτε να κάνετε με αυτό; Τίποτα…
Οι ακόλουθες λέξεις-κλειδιά: «πολλαπλασιάζεται με τον ίδιο μη μηδενικό αριθμό».
Αυτός ο ίδιος αριθμός έχει επίσης το δικό του ειδικό όνομα - παρονομαστής μιας γεωμετρικής προόδου. Ας αρχίσουμε να βγαίνουμε.)
Ο παρονομαστής μιας γεωμετρικής προόδου.
Όλα είναι απλά.
Ο παρονομαστής μιας γεωμετρικής προόδου είναι ένας μη μηδενικός αριθμός (ή τιμή) που δείχνειπόσες φορέςκάθε μέλος της προόδου περισσότερο από το προηγούμενο.
Και πάλι, κατ' αναλογία με την αριθμητική πρόοδο, η λέξη κλειδί που πρέπει να δοθεί προσοχή σε αυτόν τον ορισμό είναι η λέξη "περισσότερο". Σημαίνει ότι λαμβάνεται κάθε όρος μιας γεωμετρικής προόδου πολλαπλασιασμόςσε αυτόν ακριβώς τον παρονομαστή προηγούμενο μέλος.
Εξηγώ.
Για να υπολογίσουμε, ας πούμε δεύτεροςμέλος να πάρει ο πρώτοςμέλος και πολλαπλασιάζωτο στον παρονομαστή. Για υπολογισμό δέκατοςμέλος να πάρει ένατοςμέλος και πολλαπλασιάζωτο στον παρονομαστή.
Ο παρονομαστής της ίδιας της γεωμετρικής προόδου μπορεί να είναι οτιδήποτε. Απολύτως οποιοσδήποτε! Ακέραιος, κλασματικός, θετικός, αρνητικός, παράλογος - όλοι. Εκτός από το μηδέν. Αυτό μας λέει η λέξη «μη μηδέν» στον ορισμό. Γιατί χρειάζεται αυτή η λέξη εδώ - περισσότερα για αυτό αργότερα.
Παρονομαστής γεωμετρικής προόδουσυνήθως υποδηλώνεται με ένα γράμμα q.
Πώς να βρείτε αυτό q? Κανένα πρόβλημα! Πρέπει να λάβουμε οποιονδήποτε όρο της προόδου και διαιρέστε με τον προηγούμενο όρο. Διαίρεση είναι κλάσμα. Εξ ου και το όνομα - "ο παρονομαστής της προόδου". Ο παρονομαστής, συνήθως κάθεται σε κλάσμα, ναι ...) Αν και, λογικά, η τιμή qπρέπει να κληθεί ιδιωτικόςγεωμετρική πρόοδος, παρόμοια με διαφοράγια μια αριθμητική πρόοδο. Αλλά συμφώνησε να τηλεφωνήσει παρονομαστής. Και δεν θα επανεφεύρουμε ούτε τον τροχό.)
Ας ορίσουμε, για παράδειγμα, την τιμή qγια αυτή τη γεωμετρική πρόοδο:
2, 6, 18, 54, …
Όλα είναι στοιχειώδη. Παίρνουμε όποιοςαριθμός ακολουθίας. Αυτό που θέλουμε είναι αυτό που παίρνουμε. Εκτός από το πρώτο. Για παράδειγμα, 18. Και διαιρέστε με προηγούμενος αριθμός. Δηλαδή στις 6.
Παίρνουμε:
q = 18/6 = 3
Αυτό είναι όλο. Αυτή είναι η σωστή απάντηση. Για μια δεδομένη γεωμετρική πρόοδο, ο παρονομαστής είναι τρεις.
Ας βρούμε τον παρονομαστή qγια μια άλλη γεωμετρική πρόοδο. Για παράδειγμα, όπως αυτό:
1, -2, 4, -8, 16, …
Ολα τα ίδια. Ό,τι σημάδια έχουν τα ίδια τα μέλη, εμείς εξακολουθούμε να παίρνουμε όποιοςαύξοντα αριθμό (για παράδειγμα, 16) και διαιρέστε με προηγούμενος αριθμός(δηλαδή -8).
Παίρνουμε:
ρε = 16/(-8) = -2
Και αυτό ήταν.) Αυτή τη φορά ο παρονομαστής της εξέλιξης αποδείχθηκε αρνητικός. Μείον δύο. Συμβαίνει.)
Ας πάρουμε αυτή την εξέλιξη:
1, 1/3, 1/9, 1/27, …
Και πάλι, ανεξάρτητα από τον τύπο των αριθμών της ακολουθίας (άρτιος ακέραιος, άρτιος κλασματικός, άρτιος αρνητικός, ακόμη και παράλογος), παίρνουμε οποιονδήποτε αριθμό (για παράδειγμα, 1/9) και διαιρούμε με τον προηγούμενο αριθμό (1/3). Σύμφωνα με τους κανόνες πράξεων με κλάσματα, φυσικά.
Παίρνουμε:
Αυτό είναι όλο.) Εδώ ο παρονομαστής αποδείχθηκε κλασματικός: q = 1/3.
Αλλά μια τέτοια «πρόοδος» όπως εσείς;
3, 3, 3, 3, 3, …
Προφανώς εδώ q = 1 . Τυπικά, αυτό είναι επίσης μια γεωμετρική πρόοδος, μόνο με ίδια μέλη.) Αλλά τέτοιες προόδους δεν είναι ενδιαφέρουσες για μελέτη και πρακτική εφαρμογή. Ακριβώς όπως προόδους με συμπαγή μηδενικά. Επομένως, δεν θα τα εξετάσουμε.
Όπως μπορείτε να δείτε, ο παρονομαστής της προόδου μπορεί να είναι οτιδήποτε - ακέραιος, κλασματικός, θετικός, αρνητικός - οτιδήποτε! Δεν μπορεί απλώς να είναι μηδέν. Δεν μαντέψατε γιατί;
Λοιπόν, ας δούμε κάποιο συγκεκριμένο παράδειγμα, τι θα συμβεί αν πάρουμε ως παρονομαστή qμηδέν.) Ας έχουμε, για παράδειγμα, σι 1 = 2 , ένα q = 0 . Ποια θα είναι η δεύτερη θητεία τότε;
Πιστεύουμε:
σι 2 = σι 1 · q= 2 0 = 0
Και το τρίτο μέλος;
σι 3 = σι 2 · q= 0 0 = 0
Τύποι και συμπεριφορά γεωμετρικών προόδων.
Με όλα ήταν λίγο πολύ σαφές: αν η διαφορά στην εξέλιξη ρεείναι θετική, η εξέλιξη αυξάνεται. Εάν η διαφορά είναι αρνητική, τότε η εξέλιξη μειώνεται. Υπάρχουν μόνο δύο επιλογές. Δεν υπάρχει τρίτο.)
Αλλά με τη συμπεριφορά μιας γεωμετρικής προόδου, όλα θα είναι πολύ πιο ενδιαφέροντα και διαφορετικά!)
Μόλις τα μέλη συμπεριφέρονται εδώ: αυξάνονται και μειώνονται, και πλησιάζουν το μηδέν επ' αόριστον, ακόμη και αλλάζουν πρόσημα, ορμώντας εναλλάξ είτε στο «συν» ή στο «πλην»! Και μέσα σε όλη αυτή την ποικιλομορφία πρέπει να μπορεί κανείς να καταλάβει καλά, ναι...
Καταλαβαίνουμε;) Ας ξεκινήσουμε με την πιο απλή περίπτωση.
Ο παρονομαστής είναι θετικός ( q >0)
Με έναν θετικό παρονομαστή, πρώτον, τα μέλη μιας γεωμετρικής προόδου μπορούν να εισέλθουν συν το άπειρο(δηλαδή αυξάνεται επ' αόριστον) και μπορεί να μπει σε μείον το άπειρο(δηλαδή μειώνεται επ' αόριστον). Έχουμε ήδη συνηθίσει σε τέτοιες συμπεριφορές προόδου.
Για παράδειγμα:
(b n): 1, 2, 4, 8, 16, …
Όλα είναι απλά εδώ. Κάθε μέλος της προόδου είναι περισσότερο από το προηγούμενο. Και κάθε μέλος παίρνει πολλαπλασιασμόςπροηγούμενο μέλος στο θετικόςαριθμός +2 (δηλ. q = 2 ). Η συμπεριφορά μιας τέτοιας εξέλιξης είναι προφανής: όλα τα μέλη της προόδου μεγαλώνουν απεριόριστα, πηγαίνοντας στο διάστημα. Συν το άπειρο...
Εδώ είναι τώρα η εξέλιξη:
(b n): -1, -2, -4, -8, -16, …
Και εδώ λαμβάνεται κάθε όρος της προόδου πολλαπλασιασμόςπροηγούμενο μέλος στο θετικόςαριθμός +2. Αλλά η συμπεριφορά μιας τέτοιας προόδου είναι ήδη ακριβώς αντίθετη: κάθε μέλος της προόδου λαμβάνεται λιγότερο από το προηγούμενο, και όλοι οι όροι του μειώνονται επ' αόριστον, πηγαίνοντας στο μείον το άπειρο.
Τώρα ας σκεφτούμε: τι κοινό έχουν αυτές οι δύο προόδους; Σωστά, παρονομαστής! Εδώ και εκεί q = +2 . Θετικός αριθμός.Δυάρι. Αλλά η ΣΥΜΠΕΡΙΦΟΡΑΑυτές οι δύο προόδους είναι θεμελιωδώς διαφορετικές! Δεν μάντεψε γιατί; Ναί! Πρόκειται για πρώτο μέλος!Είναι αυτός, όπως λένε, που παραγγέλνει τη μουσική.) Δείτε μόνοι σας.
Στην πρώτη περίπτωση, ο πρώτος όρος της προόδου θετικός(+1) και, επομένως, όλοι οι επόμενοι όροι που λαμβάνονται πολλαπλασιάζοντας με θετικόςπαρονομαστής q = +2 , επίσης θα θετικός.
Αλλά στη δεύτερη περίπτωση, τον πρώτο όρο αρνητικός(-ένας). Επομένως, όλα τα επόμενα μέλη της προόδου προέκυψαν πολλαπλασιάζοντας με θετικός q = +2 , θα ληφθεί επίσης αρνητικός.Για το "μείον" στο "συν" πάντα δίνει "μείον", ναι.)
Όπως μπορείτε να δείτε, σε αντίθεση με μια αριθμητική πρόοδο, μια γεωμετρική πρόοδος μπορεί να συμπεριφέρεται με εντελώς διαφορετικούς τρόπους, όχι μόνο ανάλογα από τον παρονομαστήq, αλλά και ανάλογα από το πρώτο μέλος, Ναί.)
Θυμηθείτε: η συμπεριφορά μιας γεωμετρικής προόδου καθορίζεται μοναδικά από το πρώτο μέλος της σι 1 και παρονομαστήςq .
Και τώρα ξεκινάμε την ανάλυση λιγότερο γνωστών, αλλά πολύ πιο ενδιαφέρων περιπτώσεων!
Πάρτε, για παράδειγμα, την ακόλουθη σειρά:
(b n): 1, 1/2, 1/4, 1/8, 1/16, …
Αυτή η ακολουθία είναι επίσης μια γεωμετρική πρόοδος! Κάθε μέλος αυτής της προόδου λαμβάνεται επίσης πολλαπλασιασμόςτον προηγούμενο όρο, κατά τον ίδιο αριθμό. Μόνο ο αριθμός είναι κλασματικός: q = +1/2 . Ή +0,5 . Και (σημαντικό!) νούμερο, μικρότερο:q = 1/2<1.
Τι είναι ενδιαφέρον για αυτή τη γεωμετρική πρόοδο; Πού πάνε τα μέλη του; Ας δούμε:
1/2 = 0,5;
1/4 = 0,25;
1/8 = 0,125;
1/16 = 0,0625;
…….
Τι είναι ενδιαφέρον εδώ; Πρώτον, η μείωση των μελών της προόδου είναι αμέσως εντυπωσιακή: καθένα από τα μέλη της πιο λιγοτο προηγούμενο ακριβώς 2 φορές.Ή, σύμφωνα με τον ορισμό μιας γεωμετρικής προόδου, κάθε όρος περισσότεροπροηγούμενος 1/2 φορές, επειδή παρονομαστής προόδου q = 1/2 . Και από τον πολλαπλασιασμό με έναν θετικό αριθμό μικρότερο από ένα, το αποτέλεσμα συνήθως μειώνεται, ναι ...
Τι Ακόμημπορεί να φανεί στη συμπεριφορά αυτής της εξέλιξης; Εξαφανίζονται τα μέλη του; απεριόριστος, πηγαίνοντας στο μείον άπειρο; Δεν! Εξαφανίζονται με έναν ιδιαίτερο τρόπο. Στην αρχή μειώνονται αρκετά γρήγορα και μετά όλο και πιο αργά. Και όλη την ώρα μένοντας θετικός. Αν και πολύ, πολύ μικρό. Και για τι προσπαθούν; Δεν μάντεψε; Ναί! Τείνουν στο μηδέν!) Και, προσέξτε, τα μέλη της προόδου μας ποτέ μην φτάσεις!Μόνο απείρως κοντά του. Είναι πολύ σημαντικό.)
Μια παρόμοια κατάσταση θα είναι σε μια τέτοια εξέλιξη:
(b n): -1, -1/2, -1/4, -1/8, -1/16, …
Εδώ σι 1 = -1 , ένα q = 1/2 . Όλα είναι ίδια, μόνο που τώρα τα μέλη θα πλησιάσουν το μηδέν από την άλλη πλευρά, από κάτω. Μένοντας όλη την ώρα αρνητικός.)
Μια τέτοια γεωμετρική πρόοδος, τα μέλη της οποίας πλησιάζει το μηδέν επ' αόριστον.(δεν έχει σημασία, από τη θετική ή την αρνητική πλευρά), στα μαθηματικά έχει ένα ειδικό όνομα - απείρως φθίνουσα γεωμετρική πρόοδο.Αυτή η εξέλιξη είναι τόσο ενδιαφέρουσα και ασυνήθιστη που θα είναι ακόμη και ξεχωριστό μάθημα .)
Λοιπόν, εξετάσαμε όλα τα πιθανά θετικόςοι παρονομαστές είναι τόσο μεγάλοι όσο και μικρότεροι. Δεν θεωρούμε το ίδιο το ένα ως παρονομαστή για τους λόγους που αναφέρθηκαν παραπάνω (θυμηθείτε το παράδειγμα με την ακολουθία των τριπλών ...)
Να συνοψίσουμε:
θετικόςκαι ΠΕΡΙΣΣΟΤΕΡΑ ΑΠΟ ΕΝΑ (q>1), τότε τα μέλη της προόδου:
ένα) αυξάνονται επ' αόριστον (ανσι 1 >0);
β) μειώνεται επ' αόριστον (ανσι 1 <0).
Αν ο παρονομαστής μιας γεωμετρικής προόδου θετικός και λιγότερο από ένα (0< q<1), то члены прогрессии:
α) απείρως κοντά στο μηδέν πάνω από(ανσι 1 >0);
β) απείρως κοντά στο μηδέν από κάτω(ανσι 1 <0).
Μένει τώρα να εξετάσουμε την υπόθεση αρνητικός παρονομαστής.
Ο παρονομαστής είναι αρνητικός ( q <0)
Δεν θα πάμε μακριά για παράδειγμα. Γιατί, μάλιστα, δασύτριχη γιαγιά;!) Ας είναι, για παράδειγμα, το πρώτο μέλος της εξέλιξης σι 1 = 1 , και πάρτε τον παρονομαστή q = -2.
Παίρνουμε την ακόλουθη σειρά:
(b n): 1, -2, 4, -8, 16, …
Και ούτω καθεξής.) Λαμβάνεται κάθε όρος της προόδου πολλαπλασιασμόςπροηγούμενο μέλος στο αρνητικός αριθμός-2. Σε αυτήν την περίπτωση, όλα τα μέλη σε μονές θέσεις (πρώτο, τρίτο, πέμπτο κ.λπ.) θα είναι θετικός, και σε ζυγές θέσεις (δεύτερο, τέταρτο κ.λπ.) - αρνητικός.Οι πινακίδες είναι αυστηρά παρεμβαλλόμενες. Συν-πλην-συν-πλην ... Μια τέτοια γεωμετρική πρόοδος ονομάζεται - αυξανόμενο σημάδι εναλλασσόμενο.
Πού πάνε τα μέλη του; Και πουθενά.) Ναι, σε απόλυτη τιμή (δηλαδή modulo)οι όροι της προόδου μας αυξάνονται επ' αόριστον (εξ ου και η ονομασία «αυξάνονται»). Αλλά την ίδια στιγμή, κάθε μέλος της εξέλιξης το ρίχνει εναλλάξ στη ζέστη και μετά στο κρύο. Είτε συν είτε πλην. Η πρόοδός μας κυμαίνεται... Επιπλέον, το εύρος των διακυμάνσεων αυξάνεται ραγδαία με κάθε βήμα, ναι.) Επομένως, οι φιλοδοξίες των μελών του progression να πάνε κάπου ΕΙΔΙΚΑεδώ όχι.Ούτε στο συν άπειρο, ούτε στο μείον άπειρο, ούτε στο μηδέν - πουθενά.
Εξετάστε τώρα κάποιο κλασματικό παρονομαστή μεταξύ μηδέν και πλην ενός.
Για παράδειγμα, ας είναι σι 1 = 1 , ένα q = -1/2.
Τότε παίρνουμε την εξέλιξη:
(b n): 1, -1/2, 1/4, -1/8, 1/16, …
Και πάλι έχουμε εναλλαγή πινακίδων! Όμως, σε αντίθεση με το προηγούμενο παράδειγμα, εδώ υπάρχει ήδη μια σαφής τάση οι όροι να πλησιάζουν το μηδέν.) Μόνο που αυτή τη φορά οι όροι μας πλησιάζουν το μηδέν όχι αυστηρά από πάνω ή κάτω, αλλά πάλι διστάζοντας. Λαμβάνοντας εναλλακτικά είτε θετικές είτε αρνητικές τιμές. Ταυτόχρονα όμως ενότητεςπλησιάζουν όλο και πιο κοντά στο αγαπημένο μηδέν.)
Αυτή η γεωμετρική πρόοδος ονομάζεται απείρως φθίνουσα εναλλασσόμενη ένδειξη.
Γιατί είναι ενδιαφέροντα αυτά τα δύο παραδείγματα; Και το γεγονός ότι και στις δύο περιπτώσεις λαμβάνει χώρα εναλλασσόμενοι χαρακτήρες!Ένα τέτοιο τσιπ είναι τυπικό μόνο για προόδους με αρνητικό παρονομαστή, ναι.) Επομένως, εάν σε κάποια εργασία δείτε μια γεωμετρική πρόοδο με εναλλασσόμενα μέλη, τότε θα γνωρίζετε ήδη σταθερά ότι ο παρονομαστής του είναι 100% αρνητικός και δεν θα κάνετε λάθος στο σημάδι.)
Παρεμπιπτόντως, στην περίπτωση ενός αρνητικού παρονομαστή, το πρόσημο του πρώτου όρου δεν επηρεάζει καθόλου τη συμπεριφορά της ίδιας της εξέλιξης. Όποιο κι αν είναι το πρόσημο του πρώτου μέλους της προόδου, σε κάθε περίπτωση, θα τηρηθεί το πρόσημο της εναλλαγής των μελών. Το όλο ερώτημα είναι μόνο σε ποια μέρη(ζυγό ή μονό) θα υπάρχουν μέλη με συγκεκριμένα πρόσημα.
Θυμάμαι:
Αν ο παρονομαστής μιας γεωμετρικής προόδου αρνητικός , τότε τα σημάδια των όρων της προόδου είναι πάντα εναλλακτικό.
Παράλληλα, τα ίδια τα μέλη:
α) αυξάνονται επ' αόριστονmodulo, ανq<-1;
β) πλησιάζει το μηδέν άπειρα αν -1< q<0 (прогрессия бесконечно убывающая).
Αυτό είναι όλο. Αναλύονται όλες οι τυπικές περιπτώσεις.)
Κατά τη διαδικασία ανάλυσης μιας ποικιλίας παραδειγμάτων γεωμετρικών προόδων, χρησιμοποιούσα περιοδικά τις λέξεις: "τείνει στο μηδέν", "τείνει στο συν το άπειρο", τείνει στο μείον το άπειρο... Δεν πειράζει.) Αυτές οι στροφές ομιλίας (και συγκεκριμένα παραδείγματα) είναι απλώς μια αρχική γνωριμία με η ΣΥΜΠΕΡΙΦΟΡΑδιάφορες ακολουθίες αριθμών. Παράδειγμα γεωμετρικής προόδου.
Γιατί χρειάζεται να γνωρίζουμε τη συμπεριφορά προόδου; Τι διαφορά έχει που πάει; Στο μηδέν, στο συν άπειρο, στο μείον το άπειρο ... Τι μας νοιάζει αυτό;
Το θέμα είναι ότι ήδη στο πανεπιστήμιο, στο μάθημα των ανώτερων μαθηματικών, θα χρειαστείτε την ικανότητα να εργαστείτε με μια ποικιλία αριθμητικών ακολουθιών (με οποιεσδήποτε, όχι μόνο προόδους!) Και την ικανότητα να φανταστείτε ακριβώς πώς συμπεριφέρεται αυτή ή εκείνη η ακολουθία - είτε αυξάνεται απεριόριστα, είτε μειώνεται, είτε τείνει σε έναν συγκεκριμένο αριθμό (και όχι απαραίτητα στο μηδέν), είτε ακόμη δεν τείνει σε τίποτα... Μια ολόκληρη ενότητα είναι αφιερωμένη σε αυτό το θέμα κατά τη διάρκεια των μαθηματικών ανάλυση - οριακή θεωρία.Λίγο πιο συγκεκριμένα, το concept όριο της ακολουθίας αριθμών.Πολύ ενδιαφέρον θέμα! Είναι λογικό να πας στο κολέγιο και να το καταλάβεις.)
Μερικά παραδείγματα από αυτήν την ενότητα (ακολουθίες που έχουν όριο) και συγκεκριμένα, απείρως φθίνουσα γεωμετρική πρόοδοαρχίσουν να μαθαίνουν στο σχολείο. Συνηθίζω.)
Επιπλέον, η ικανότητα να μελετάς καλά τη συμπεριφορά των ακολουθιών στο μέλλον θα είναι πολύ χρήσιμη και θα είναι πολύ χρήσιμη σε έρευνα λειτουργίας.Το πιο ποικίλο. Αλλά η ικανότητα να εργάζεστε σωστά με συναρτήσεις (υπολογισμός παραγώγων, εξερεύνησή τους πλήρως, δημιουργία γραφημάτων τους) ήδη αυξάνει δραματικά το μαθηματικό σας επίπεδο! Αμφιβολία? Δεν χρειάζεται. Θυμηθείτε επίσης τα λόγια μου.)
Ας δούμε μια γεωμετρική πρόοδο στη ζωή;
Στη ζωή γύρω μας, συναντάμε εκθετική εξέλιξη πολύ, πολύ συχνά. Χωρίς καν να το ξέρω.)
Για παράδειγμα, διάφοροι μικροοργανισμοί που μας περιβάλλουν παντού σε τεράστιες ποσότητες και τους οποίους δεν βλέπουμε καν χωρίς μικροσκόπιο πολλαπλασιάζονται με ακρίβεια σε γεωμετρική πρόοδο.
Ας πούμε ότι ένα βακτήριο αναπαράγεται με διαίρεση στο μισό, δίνοντας απογόνους σε 2 βακτήρια. Με τη σειρά τους, καθένα από αυτά, πολλαπλασιάζοντας, διαιρείται επίσης στο μισό, δίνοντας έναν κοινό απόγονο 4 βακτηρίων. Η επόμενη γενιά θα δώσει 8 βακτήρια, μετά 16 βακτήρια, 32, 64 και ούτω καθεξής. Με κάθε διαδοχική γενιά, ο αριθμός των βακτηρίων διπλασιάζεται. Χαρακτηριστικό παράδειγμα γεωμετρικής προόδου.)
Επίσης, μερικά έντομα - αφίδες, μύγες - πολλαπλασιάζονται εκθετικά. Και τα κουνέλια μερικές φορές, παρεμπιπτόντως, επίσης.)
Ένα άλλο παράδειγμα γεωμετρικής προόδου, πιο κοντά στην καθημερινή ζωή, είναι το λεγόμενο ανατοκισμός.Ένα τέτοιο ενδιαφέρον φαινόμενο συναντάται συχνά στις τραπεζικές καταθέσεις και ονομάζεται κεφαλαιοποίηση τόκων.Τι είναι?
Εσείς ο ίδιος είστε ακόμα, φυσικά, νέος. Σπουδάζεις στο σχολείο, δεν κάνεις αίτηση στις τράπεζες. Αλλά οι γονείς σου είναι ενήλικες και ανεξάρτητοι άνθρωποι. Πηγαίνουν στη δουλειά, κερδίζουν χρήματα για το καθημερινό τους ψωμί και βάζουν μερικά από τα χρήματα στην τράπεζα, κάνοντας αποταμιεύσεις.)
Ας υποθέσουμε ότι ο μπαμπάς σας θέλει να εξοικονομήσει ένα ορισμένο ποσό χρημάτων για οικογενειακές διακοπές στην Τουρκία και να βάλει 50.000 ρούβλια στην τράπεζα με 10% ετησίως για μια περίοδο τριών ετών με ετήσια κεφαλαιοποίηση τόκων.Επιπλέον, δεν μπορεί να γίνει τίποτα με την κατάθεση όλη αυτή την περίοδο. Δεν μπορείτε ούτε να αναπληρώσετε την κατάθεση ούτε να κάνετε ανάληψη χρημάτων από τον λογαριασμό. Τι κέρδος θα έχει σε αυτά τα τρία χρόνια;
Λοιπόν, πρώτα, πρέπει να υπολογίσετε ποιο είναι το 10% ετησίως. Αυτό σημαίνει ότι σε ένα χρόνο 10% θα προστεθεί στο αρχικό ποσό κατάθεσης από την τράπεζα. Από τι? Φυσικά, από αρχικό ποσό κατάθεσης.
Υπολογίστε το ποσό του λογαριασμού σε ένα έτος. Εάν το αρχικό ποσό της κατάθεσης ήταν 50.000 ρούβλια (δηλαδή 100%), τότε σε ένα χρόνο πόσος τόκος θα είναι ο λογαριασμός; Σωστά, 110%! Από 50.000 ρούβλια.
Επομένως, θεωρούμε το 110% των 50.000 ρούβλια:
50.000 1,1 \u003d 55.000 ρούβλια.
Ελπίζω να καταλαβαίνετε ότι η εύρεση του 110% της τιμής σημαίνει πολλαπλασιασμός αυτής της τιμής με τον αριθμό 1,1; Αν δεν καταλαβαίνετε γιατί συμβαίνει αυτό, θυμηθείτε την πέμπτη και την έκτη τάξη. Και συγκεκριμένα - η σχέση των ποσοστών με τα κλάσματα και τα μέρη.)
Έτσι, η αύξηση για το πρώτο έτος θα είναι 5000 ρούβλια.
Πόσα χρήματα θα υπάρχουν στον λογαριασμό μετά από δύο χρόνια; 60.000 ρούβλια; Δυστυχώς (ή μάλλον, ευτυχώς), δεν είναι τόσο απλό. Το όλο κόλπο της κεφαλαιοποίησης τόκων είναι ότι με κάθε νέο δεδουλευμένο τόκο, αυτοί οι ίδιοι τόκοι θα λαμβάνονται ήδη υπόψη από το νέο ποσό!Από αυτόν που ήδηείναι σε λογαριασμό Επί του παρόντος.Και οι δεδουλευμένοι τόκοι της προηγούμενης περιόδου προστίθενται στο αρχικό ποσό της κατάθεσης και, έτσι, συμμετέχουν και οι ίδιοι στον υπολογισμό των νέων τόκων! Δηλαδή γίνονται πλήρες μέρος του συνολικού λογαριασμού. ή γενικά κεφάλαιο.Εξ ου και το όνομα - κεφαλαιοποίηση τόκων.
Είναι στην οικονομία. Και στα μαθηματικά τέτοια ποσοστά λέγονται ανατοκισμός.Ή τοις εκατό του τοις εκατό.) Το κόλπο τους είναι ότι στον διαδοχικό υπολογισμό υπολογίζονται κάθε φορά τα ποσοστά από τη νέα τιμή.Όχι από το πρωτότυπο...
Επομένως, προκειμένου να υπολογιστεί το άθροισμα μέσω δύο χρόνια, πρέπει να υπολογίσουμε το 110% του ποσού που θα μπει στον λογαριασμό σε ένα χρόνο.Δηλαδή, ήδη από 55.000 ρούβλια.
Θεωρούμε το 110% των 55.000 ρούβλια:
55000 1,1 \u003d 60500 ρούβλια.
Αυτό σημαίνει ότι η ποσοστιαία αύξηση για το δεύτερο έτος θα είναι ήδη 5.500 ρούβλια και για δύο χρόνια - 10.500 ρούβλια.
Τώρα μπορείτε ήδη να μαντέψετε ότι σε τρία χρόνια το ποσό στον λογαριασμό θα είναι 110% των 60.500 ρούβλια. Δηλαδή πάλι 110% από το προηγούμενο (πέρυσι)ποσά.
Εδώ θεωρούμε:
60500 1,1 \u003d 66550 ρούβλια.
Και τώρα χτίζουμε τα χρηματικά μας ποσά ανά χρόνια με τη σειρά:
50000;
55000 = 50000 1,1;
60500 = 55000 1,1 = (50000 1,1) 1,1;
66550 = 60500 1,1 = ((50000 1,1) 1,1) 1,1
Πώς είναι λοιπόν; Γιατί όχι μια γεωμετρική πρόοδο; Πρώτο μέλος σι 1 = 50000 , και ο παρονομαστής q = 1,1 . Κάθε όρος είναι αυστηρά 1,1 φορές μεγαλύτερος από τον προηγούμενο. Όλα είναι αυστηρά σύμφωνα με τον ορισμό.)
Και πόσα επιπλέον ποσοστά μπόνους θα «πέσει» ο μπαμπάς σας ενώ τα 50.000 ρούβλια του ήταν στον τραπεζικό λογαριασμό για τρία χρόνια;
Πιστεύουμε:
66550 - 50000 = 16550 ρούβλια
Είναι κακό, φυσικά. Αλλά αυτό συμβαίνει εάν το αρχικό ποσό της εισφοράς είναι μικρό. Κι αν υπάρχουν περισσότερα; Ας πούμε, όχι 50, αλλά 200 χιλιάδες ρούβλια; Στη συνέχεια, η αύξηση για τρία χρόνια θα είναι ήδη 66.200 ρούβλια (αν μετρήσετε). Το οποίο είναι ήδη πολύ καλό.) Και αν η συμβολή είναι ακόμη μεγαλύτερη; Αυτό είναι...
Συμπέρασμα: όσο μεγαλύτερη είναι η αρχική συνεισφορά, τόσο πιο κερδοφόρα γίνεται η κεφαλαιοποίηση των τόκων. Γι' αυτό οι καταθέσεις με κεφαλαιοποίηση τόκων παρέχονται από τις τράπεζες για μεγάλες περιόδους. Ας πούμε πέντε χρόνια.
Επίσης, κάθε είδους κακές ασθένειες όπως η γρίπη, η ιλαρά και ακόμη πιο τρομερές ασθένειες (το ίδιο SARS στις αρχές της δεκαετίας του 2000 ή η πανούκλα στον Μεσαίωνα) αρέσει να εξαπλώνονται εκθετικά. Εξ ου και η κλίμακα των επιδημιών, ναι...) Και όλα αυτά λόγω του γεγονότος ότι μια γεωμετρική εξέλιξη με ολόκληρος θετικός παρονομαστής (q>1) - κάτι που μεγαλώνει πολύ γρήγορα! Θυμηθείτε την αναπαραγωγή των βακτηρίων: από ένα βακτήριο λαμβάνονται δύο, από δύο - τέσσερα, από τέσσερα - οκτώ και ούτω καθεξής ... Με την εξάπλωση οποιασδήποτε μόλυνσης, όλα είναι ίδια.)
Τα απλούστερα προβλήματα στη γεωμετρική πρόοδο.
Ας ξεκινήσουμε, όπως πάντα, με ένα απλό πρόβλημα. Καθαρά για να καταλάβεις το νόημα.
1. Είναι γνωστό ότι ο δεύτερος όρος μιας γεωμετρικής προόδου είναι 6 και ο παρονομαστής είναι -0,5. Βρείτε τον πρώτο, τον τρίτο και τον τέταρτο όρο.
Μας δίνονται λοιπόν ατελείωτεςγεωμετρική πρόοδος, πολύ γνωστή δεύτερη περίοδοςαυτή η εξέλιξη:
b2 = 6
Επιπλέον, γνωρίζουμε επίσης παρονομαστής προόδου:
q = -0,5
Και πρέπει να βρεις πρώτος, τρίτοςκαι τέταρτοςμέλη αυτής της εξέλιξης.
Εδώ ενεργούμε. Καταγράφουμε την ακολουθία ανάλογα με την κατάσταση του προβλήματος. Άμεσα σε γενικούς όρους, όπου το δεύτερο μέλος είναι τα έξι:
b1,6,σι 3 , σι 4 , …
Τώρα ας αρχίσουμε να ψάχνουμε. Ξεκινάμε, όπως πάντα, με τα πιο απλά. Μπορείτε να υπολογίσετε, για παράδειγμα, τον τρίτο όρο β 3? Μπορώ! Γνωρίζουμε ήδη (απευθείας με την έννοια της γεωμετρικής προόδου) ότι ο τρίτος όρος (β 3)περισσότερο από ένα δευτερόλεπτο (σι 2 ) σε "q"μια φορά!
Γράφουμε λοιπόν:
b 3 =σι 2 · q
Αντικαθιστούμε το έξι σε αυτήν την έκφραση αντί για β 2και -0,5 αντί qκαι σκεφτόμαστε. Και το μείον επίσης δεν αγνοείται, φυσικά ...
b 3 \u003d 6 (-0,5) \u003d -3
Σαν αυτό. Η τρίτη θητεία αποδείχθηκε αρνητική. Δεν είναι περίεργο: ο παρονομαστής μας q- αρνητικό. Και το συν πολλαπλασιασμένο με το μείον, θα είναι, φυσικά, μείον.)
Εξετάζουμε τώρα τον επόμενο, τέταρτο όρο της προόδου:
b 4 =σι 3 · q
b 4 \u003d -3 (-0,5) \u003d 1,5
Η τέταρτη περίοδος είναι και πάλι με ένα συν. Ο πέμπτος όρος θα είναι πάλι με ένα μείον, ο έκτος με ένα συν, και ούτω καθεξής. Σημάδια - εναλλακτικά!
Έτσι, βρέθηκαν το τρίτο και το τέταρτο μέλος. Το αποτέλεσμα είναι η ακόλουθη σειρά:
b1; 6; -3; 1,5; …
Μένει τώρα να βρούμε τον πρώτο όρο β 1σύμφωνα με το γνωστό δεύτερο. Για να το κάνουμε αυτό, βαδίζουμε προς την άλλη κατεύθυνση, προς τα αριστερά. Αυτό σημαίνει ότι σε αυτή την περίπτωση, δεν χρειάζεται να πολλαπλασιάσουμε τον δεύτερο όρο της προόδου με τον παρονομαστή, αλλά μερίδιο.
Χωρίζουμε και παίρνουμε:
![]()
Αυτό είναι όλο.) Η απάντηση στο πρόβλημα θα είναι η εξής:
-12; 6; -3; 1,5; …
Όπως μπορείτε να δείτε, η αρχή της λύσης είναι η ίδια όπως στο . Ξέρουμε όποιοςμέλος και παρονομαστήςγεωμετρική πρόοδος - μπορούμε να βρούμε οποιονδήποτε άλλο όρο. Ό,τι θέλουμε, θα το βρούμε.) Η μόνη διαφορά είναι ότι η πρόσθεση/αφαίρεση αντικαθίσταται από πολλαπλασιασμό/διαίρεση.
Θυμηθείτε: εάν γνωρίζουμε τουλάχιστον ένα μέλος και παρονομαστή μιας γεωμετρικής προόδου, τότε μπορούμε πάντα να βρούμε οποιοδήποτε άλλο μέλος αυτής της προόδου.
Η ακόλουθη εργασία, σύμφωνα με την παράδοση, προέρχεται από την πραγματική έκδοση του OGE:
2.
… 150; Χ; 6; 1.2; …
Πώς είναι λοιπόν; Αυτή τη φορά δεν υπάρχει πρώτος όρος, ούτε παρονομαστής q, δίνεται απλώς μια ακολουθία αριθμών ... Κάτι γνωστό ήδη, σωστά; Ναί! Ένα παρόμοιο πρόβλημα έχει ήδη αντιμετωπιστεί στην αριθμητική πρόοδο!
Εδώ δεν φοβόμαστε. Ολα τα ίδια. Γυρίστε το κεφάλι σας και θυμηθείτε τη στοιχειώδη έννοια μιας γεωμετρικής προόδου. Εξετάζουμε προσεκτικά την ακολουθία μας και καταλαβαίνουμε ποιες παράμετροι της γεωμετρικής προόδου των τριών κύριων (πρώτο μέλος, παρονομαστής, αριθμός μέλους) κρύβονται σε αυτήν.
Αριθμοί μελών; Δεν υπάρχουν αριθμοί μελών, ναι... Αλλά υπάρχουν τέσσερα διαδοχικόςαριθμοί. Τι σημαίνει αυτή η λέξη, δεν βλέπω το νόημα να το εξηγήσω σε αυτό το στάδιο.) Υπάρχουν δύο γειτονικοί γνωστοί αριθμοί;Υπάρχει! Αυτά είναι τα 6 και 1.2. Έτσι μπορούμε να βρούμε παρονομαστής προόδου.Παίρνουμε λοιπόν τον αριθμό 1.2 και διαιρούμε στον προηγούμενο αριθμό.Για έξι.
Παίρνουμε:
Παίρνουμε:
Χ= 150 0,2 = 30
Απάντηση: Χ = 30 .
Όπως μπορείτε να δείτε, όλα είναι πολύ απλά. Η κύρια δυσκολία έγκειται μόνο στους υπολογισμούς. Είναι ιδιαίτερα δύσκολο στην περίπτωση αρνητικών και κλασματικών παρονομαστών. Όσοι έχετε προβλήματα λοιπόν, επαναλάβετε την αριθμητική! Πώς να δουλεύεις με κλάσματα, πώς να δουλεύεις με αρνητικούς αριθμούς κ.ο.κ... Διαφορετικά, εδώ θα επιβραδύνεις αλύπητα.
Τώρα ας αλλάξουμε λίγο το πρόβλημα. Τώρα θα έχει ενδιαφέρον! Ας αφαιρέσουμε τον τελευταίο αριθμό 1.2 σε αυτό. Ας λύσουμε αυτό το πρόβλημα τώρα:
3. Αρκετοί διαδοχικοί όροι μιας γεωμετρικής προόδου καταγράφονται:
… 150; Χ; 6; …
Να βρείτε τον όρο της προόδου, που συμβολίζεται με το γράμμα x.
Όλα είναι ίδια, μόνο δύο γειτονικές διάσημοςδεν έχουμε πλέον μέλη της προόδου. Αυτό είναι το κύριο πρόβλημα. Γιατί το μέγεθος qμέσω δύο γειτονικών όρων, μπορούμε ήδη να προσδιορίσουμε εύκολα δεν μπορούμε.Έχουμε την ευκαιρία να ανταποκριθούμε στην πρόκληση; Φυσικά!
Ας γράψουμε τον άγνωστο όρο" Χ«Αμεσα με την έννοια της γεωμετρικής προόδου!Σε γενικές γραμμές.
Ναι ναι! Απευθείας με άγνωστο παρονομαστή!
Από τη μία πλευρά, για το x μπορούμε να γράψουμε την ακόλουθη αναλογία:
Χ= 150q
Από την άλλη πλευρά, έχουμε κάθε δικαίωμα να ζωγραφίσουμε το ίδιο Χ μέσα Επόμενομέλος, μέσω των έξι! Διαιρέστε το έξι με τον παρονομαστή.
Σαν αυτό:
Χ = 6/ q
Προφανώς, τώρα μπορούμε να εξισώσουμε και τους δύο αυτούς λόγους. Αφού εκφραζόμαστε το ίδιοτιμή (x), αλλά δύο διαφορετικοί τρόποι.
Παίρνουμε την εξίσωση:
Πολλαπλασιάζοντας τα πάντα με q, απλοποιώντας, μειώνοντας, παίρνουμε την εξίσωση:
q 2 \u003d 1/25
Λύνουμε και παίρνουμε:
q = ±1/5 = ±0,2
Ωχ! Ο παρονομαστής είναι διπλός! +0,2 και -0,2. Και ποιο να διαλέξω; Αδιέξοδο?
Ηρεμία! Ναι, το πρόβλημα έχει πραγματικά δύο λύσεις!Τίποτα λάθος με αυτό. Συμβαίνει.) Δεν εκπλήσσεσαι όταν, για παράδειγμα, παίρνεις δύο ρίζες λύνοντας το συνηθισμένο; Είναι η ίδια ιστορία εδώ.)
Για q = +0,2θα πάρουμε:
X \u003d 150 0,2 \u003d 30
Και για q = -0,2 θα είναι:
Χ = 150 (-0,2) = -30
Παίρνουμε διπλή απάντηση: Χ = 30; Χ = -30.
Τι σημαίνει αυτό το ενδιαφέρον γεγονός; Και αυτό που υπάρχει δύο προόδους, ικανοποιώντας την κατάσταση του προβλήματος!
Όπως αυτά:
…; 150; 30; 6; …
…; 150; -30; 6; …
Και τα δύο είναι κατάλληλα.) Ποιος πιστεύετε ότι είναι ο λόγος για τον διχασμό των απαντήσεων; Μόνο και μόνο λόγω της αποβολής συγκεκριμένου μέλους της εξέλιξης (1,2), που έρχεται μετά την εξάδα. Και γνωρίζοντας μόνο το προηγούμενο (n-1)-ο και τα επόμενα (n+1)-ο μέλη της γεωμετρικής προόδου, δεν μπορούμε πλέον να πούμε κατηγορηματικά τίποτα για το ν-ο μέλος που στέκεται ανάμεσά τους. Υπάρχουν δύο επιλογές - συν και πλην.
Αλλά δεν πειράζει. Κατά κανόνα, σε εργασίες για μια γεωμετρική πρόοδο υπάρχουν πρόσθετες πληροφορίες που δίνουν μια σαφή απάντηση. Ας πούμε τα λόγια: "εναλλασσόμενη πρόοδος"ή "πρόοδος με θετικό παρονομαστή"και ούτω καθεξής... Είναι αυτές οι λέξεις που πρέπει να χρησιμεύσουν ως ένδειξη, ποιο πρόσημο, συν ή πλην, θα πρέπει να επιλεγεί κατά την τελική απάντηση. Εάν δεν υπάρχουν τέτοιες πληροφορίες, τότε - ναι, η εργασία θα έχει δύο λύσεις.)
Και τώρα αποφασίζουμε μόνοι μας.
4. Προσδιορίστε αν ο αριθμός 20 θα είναι μέλος μιας γεωμετρικής προόδου:
4 ; 6; 9; …
5. Δίνεται εναλλασσόμενη γεωμετρική πρόοδος:
…; 5; Χ ; 45; …
Βρείτε τον όρο της προόδου που υποδεικνύεται με το γράμμα Χ .
6. Βρείτε τον τέταρτο θετικό όρο της γεωμετρικής προόδου:
625; -250; 100; …
7. Ο δεύτερος όρος της γεωμετρικής προόδου είναι -360 και ο πέμπτος όρος είναι 23.04. Βρείτε τον πρώτο όρο αυτής της προόδου.
Απαντήσεις (σε αταξία): -15; 900; Οχι; 2.56.
Συγχαρητήρια αν όλα πάνε καλά!
Κάτι δεν ταιριάζει; Υπάρχει κάπου διπλή απάντηση; Διαβάσαμε προσεκτικά τους όρους της ανάθεσης!
Το τελευταίο παζλ δεν λειτουργεί; Τίποτα περίπλοκο εκεί.) Εργαζόμαστε απευθείας σύμφωνα με την έννοια μιας γεωμετρικής προόδου. Λοιπόν, μπορείτε να σχεδιάσετε μια εικόνα. Βοηθά.)
Όπως μπορείτε να δείτε, όλα είναι στοιχειώδη. Εάν η εξέλιξη είναι σύντομη. Κι αν είναι μακρύ; Ή είναι πολύ μεγάλος ο αριθμός του επιθυμητού μέλους; Θα ήθελα, κατ' αναλογία με μια αριθμητική πρόοδο, να αποκτήσω με κάποιο τρόπο έναν βολικό τύπο που να διευκολύνει την εύρεση όποιοςμέλος οποιασδήποτε γεωμετρικής προόδου από τον αριθμό του.Χωρίς να πολλαπλασιάσω πολλές, πολλές φορές q. Και υπάρχει μια τέτοια φόρμουλα!) Λεπτομέρειες - στο επόμενο μάθημα.


