Η διατήρηση του απορρήτου σας είναι σημαντική για εμάς. Για το λόγο αυτό, έχουμε αναπτύξει μια Πολιτική Απορρήτου που περιγράφει τον τρόπο με τον οποίο χρησιμοποιούμε και αποθηκεύουμε τις πληροφορίες σας. Διαβάστε τις πρακτικές απορρήτου μας και ενημερώστε μας εάν έχετε ερωτήσεις.
Συλλογή και χρήση προσωπικών πληροφοριών
Οι προσωπικές πληροφορίες αναφέρονται σε δεδομένα που μπορούν να χρησιμοποιηθούν για την αναγνώριση ή επικοινωνία με ένα συγκεκριμένο άτομο.
Ενδέχεται να σας ζητηθεί να δώσετε τα προσωπικά σας στοιχεία ανά πάσα στιγμή όταν επικοινωνήσετε μαζί μας.
Ακολουθούν ορισμένα παραδείγματα των τύπων προσωπικών πληροφοριών που ενδέχεται να συλλέγουμε και πώς μπορούμε να χρησιμοποιήσουμε αυτές τις πληροφορίες.
Ποιες προσωπικές πληροφορίες συλλέγουμε:
- Όταν υποβάλλετε μια αίτηση στον ιστότοπο, ενδέχεται να συλλέξουμε διάφορες πληροφορίες, όπως το όνομά σας, τον αριθμό τηλεφώνου, τη διεύθυνση email σας κ.λπ.
Πώς χρησιμοποιούμε τα προσωπικά σας στοιχεία:
- Οι προσωπικές πληροφορίες που συλλέγουμε μας επιτρέπουν να επικοινωνήσουμε μαζί σας με μοναδικές προσφορές, προσφορές και άλλες εκδηλώσεις και επερχόμενες εκδηλώσεις.
- Από καιρό σε καιρό, ενδέχεται να χρησιμοποιήσουμε τα προσωπικά σας στοιχεία για να στείλουμε σημαντικές ειδοποιήσεις και επικοινωνίες.
- Ενδέχεται επίσης να χρησιμοποιήσουμε προσωπικές πληροφορίες για εσωτερικούς σκοπούς, όπως διεξαγωγή ελέγχων, ανάλυση δεδομένων και διάφορες έρευνες, προκειμένου να βελτιώσουμε τις υπηρεσίες που παρέχουμε και να σας παρέχουμε συστάσεις σχετικά με τις υπηρεσίες μας.
- Εάν συμμετέχετε σε κλήρωση, διαγωνισμό ή παρόμοια προσφορά, ενδέχεται να χρησιμοποιήσουμε τις πληροφορίες που παρέχετε για τη διαχείριση τέτοιων προγραμμάτων.
Αποκάλυψη πληροφοριών σε τρίτους
Δεν αποκαλύπτουμε τις πληροφορίες που λαμβάνουμε από εσάς σε τρίτους.
Εξαιρέσεις:
- Εάν είναι απαραίτητο - σύμφωνα με το νόμο, τη δικαστική διαδικασία, σε νομικές διαδικασίες και/ή βάσει δημόσιων αιτημάτων ή αιτημάτων από κυβερνητικές αρχές στην επικράτεια της Ρωσικής Ομοσπονδίας - να αποκαλύψετε τα προσωπικά σας στοιχεία. Ενδέχεται επίσης να αποκαλύψουμε πληροφορίες σχετικά με εσάς εάν κρίνουμε ότι αυτή η αποκάλυψη είναι απαραίτητη ή κατάλληλη για λόγους ασφάλειας, επιβολής του νόμου ή άλλους σκοπούς δημόσιας σημασίας.
- Σε περίπτωση αναδιοργάνωσης, συγχώνευσης ή πώλησης, ενδέχεται να μεταφέρουμε τις προσωπικές πληροφορίες που συλλέγουμε στον αντίστοιχο τρίτο διάδοχο.
Προστασία προσωπικών πληροφοριών
Λαμβάνουμε προφυλάξεις - συμπεριλαμβανομένων διοικητικών, τεχνικών και φυσικών - για την προστασία των προσωπικών σας δεδομένων από απώλεια, κλοπή και κακή χρήση, καθώς και από μη εξουσιοδοτημένη πρόσβαση, αποκάλυψη, τροποποίηση και καταστροφή.
Σεβασμός του απορρήτου σας σε εταιρικό επίπεδο
Για να διασφαλίσουμε ότι τα προσωπικά σας στοιχεία είναι ασφαλή, κοινοποιούμε τα πρότυπα απορρήτου και ασφάλειας στους υπαλλήλους μας και εφαρμόζουμε αυστηρά τις πρακτικές απορρήτου.
Σε αυτό το άρθρο θα μιλήσουμε για παράλληλες γραμμές, θα δώσουμε ορισμούς και θα περιγράψουμε τα σημάδια και τις συνθήκες του παραλληλισμού. Για να κάνουμε το θεωρητικό υλικό πιο ξεκάθαρο, θα χρησιμοποιήσουμε απεικονίσεις και λύσεις σε τυπικά παραδείγματα.
Yandex.RTB R-A-339285-1 Ορισμός 1
Παράλληλες γραμμές σε ένα επίπεδο– δύο ευθείες σε ένα επίπεδο που δεν έχουν κοινά σημεία.
Ορισμός 2
Παράλληλες γραμμές σε τρισδιάστατο χώρο– δύο ευθείες σε τρισδιάστατο χώρο, που βρίσκονται στο ίδιο επίπεδο και δεν έχουν κοινά σημεία.
Είναι απαραίτητο να σημειωθεί ότι για τον προσδιορισμό παράλληλων γραμμών στο χώρο, η διευκρίνιση "που βρίσκεται στο ίδιο επίπεδο" είναι εξαιρετικά σημαντική: δύο γραμμές σε τρισδιάστατο χώρο που δεν έχουν κοινά σημεία και δεν βρίσκονται στο ίδιο επίπεδο δεν είναι παράλληλες. , αλλά διασταυρώνονται.
Για να υποδείξετε παράλληλες γραμμές, συνηθίζεται να χρησιμοποιείτε το σύμβολο ∥. Δηλαδή, εάν οι δεδομένες ευθείες a και b είναι παράλληλες, αυτή η συνθήκη θα πρέπει να γραφεί εν συντομία ως εξής: a ‖ b. Προφορικά, ο παραλληλισμός των ευθειών συμβολίζεται ως εξής: οι ευθείες α και β είναι παράλληλες ή η ευθεία α είναι παράλληλη προς την ευθεία β ή η ευθεία β είναι παράλληλη στην ευθεία α.
Ας διατυπώσουμε μια δήλωση που παίζει σημαντικό ρόλο στο υπό μελέτη θέμα.
Αξίωμα
Από ένα σημείο που δεν ανήκει σε μια δεδομένη ευθεία διέρχεται η μόνη ευθεία παράλληλη προς τη δεδομένη. Αυτή η δήλωση δεν μπορεί να αποδειχθεί με βάση τα γνωστά αξιώματα της επιπεδομετρίας.
Στην περίπτωση που μιλάμε για χώρο, ισχύει το θεώρημα:
Θεώρημα 1
Μέσα από οποιοδήποτε σημείο του χώρου που δεν ανήκει σε μια δεδομένη ευθεία, θα υπάρχει μια ευθεία παράλληλη προς τη δεδομένη.
Αυτό το θεώρημα είναι εύκολο να αποδειχθεί με βάση το παραπάνω αξίωμα (πρόγραμμα γεωμετρίας για τάξεις 10 - 11).
Το κριτήριο του παραλληλισμού είναι επαρκής συνθήκη, η εκπλήρωση της οποίας εγγυάται τον παραλληλισμό των ευθειών. Με άλλα λόγια, η πλήρωση αυτής της προϋπόθεσης αρκεί για να επιβεβαιώσει το γεγονός του παραλληλισμού.
Συγκεκριμένα, υπάρχουν απαραίτητες και επαρκείς προϋποθέσεις για τον παραλληλισμό των γραμμών στο επίπεδο και στο χώρο. Ας εξηγήσουμε: αναγκαίο σημαίνει η συνθήκη της οποίας η εκπλήρωση είναι απαραίτητη για παράλληλες ευθείες. αν δεν εκπληρωθεί, οι γραμμές δεν είναι παράλληλες.
Συνοψίζοντας, απαραίτητη και επαρκής προϋπόθεση για τον παραλληλισμό των ευθειών είναι μια συνθήκη η τήρηση της οποίας είναι απαραίτητη και επαρκής για να είναι παράλληλες μεταξύ τους οι ευθείες. Από τη μία πλευρά, αυτό είναι ένα σημάδι παραλληλισμού, από την άλλη πλευρά, είναι μια ιδιότητα που ενυπάρχει σε παράλληλες γραμμές.
Πριν δώσουμε την ακριβή διατύπωση μιας αναγκαίας και ικανής συνθήκης, ας θυμηθούμε μερικές επιπλέον έννοιες.
Ορισμός 3
Τέμνουσα γραμμή– μια ευθεία που τέμνει καθεμία από δύο δεδομένες μη συμπίπτουσες ευθείες.
Τέμνοντας δύο ευθείες γραμμές, ένα εγκάρσιο σχηματίζει οκτώ μη ανεπτυγμένες γωνίες. Για να διαμορφώσουμε μια απαραίτητη και επαρκή συνθήκη, θα χρησιμοποιήσουμε τέτοιους τύπους γωνιών όπως διασταυρούμενες, αντίστοιχες και μονόπλευρες. Ας τα δείξουμε στην εικόνα:
Θεώρημα 2
Εάν δύο ευθείες σε ένα επίπεδο τέμνονται από ένα εγκάρσιο, τότε για να είναι παράλληλες οι δεδομένες ευθείες είναι απαραίτητο και αρκετό οι τεμνόμενες γωνίες να είναι ίσες ή οι αντίστοιχες γωνίες να είναι ίσες ή το άθροισμα των γωνιών της μίας πλευράς να είναι ίσο με 180 μοίρες.
Ας δείξουμε γραφικά την απαραίτητη και επαρκή συνθήκη για τον παραλληλισμό των ευθειών σε ένα επίπεδο:
Η απόδειξη αυτών των συνθηκών υπάρχει στο πρόγραμμα γεωμετρίας για τις τάξεις 7 - 9.
Γενικά, αυτές οι προϋποθέσεις ισχύουν και για τον τρισδιάστατο χώρο, υπό την προϋπόθεση ότι δύο γραμμές και μια τομή ανήκουν στο ίδιο επίπεδο.
Ας υποδείξουμε μερικά ακόμη θεωρήματα που χρησιμοποιούνται συχνά για να αποδείξουν το γεγονός ότι οι ευθείες είναι παράλληλες.
Θεώρημα 3
Σε ένα επίπεδο, δύο ευθείες παράλληλες σε μια τρίτη είναι παράλληλες μεταξύ τους. Αυτό το χαρακτηριστικό αποδεικνύεται με βάση το αξίωμα του παραλληλισμού που αναφέρθηκε παραπάνω.
Θεώρημα 4
Στον τρισδιάστατο χώρο, δύο ευθείες παράλληλες προς μια τρίτη είναι παράλληλες μεταξύ τους.
Η απόδειξη ενός σημείου μελετάται στο πρόγραμμα σπουδών της Γεωμετρίας της 10ης τάξης.
Ας δώσουμε μια απεικόνιση αυτών των θεωρημάτων:
Ας υποδείξουμε ένα ακόμη ζεύγος θεωρημάτων που αποδεικνύουν τον παραλληλισμό των ευθειών.
Θεώρημα 5
Σε ένα επίπεδο, δύο ευθείες κάθετες σε μια τρίτη είναι παράλληλες μεταξύ τους.
Ας διατυπώσουμε κάτι παρόμοιο για τον τρισδιάστατο χώρο.
Θεώρημα 6
Στον τρισδιάστατο χώρο, δύο ευθείες κάθετες σε μια τρίτη είναι παράλληλες μεταξύ τους.
Ας δείξουμε:
Όλα τα παραπάνω θεωρήματα, σημεία και συνθήκες καθιστούν δυνατή την εύκολη απόδειξη του παραλληλισμού των γραμμών χρησιμοποιώντας τις μεθόδους της γεωμετρίας. Δηλαδή, για να αποδείξει κανείς τον παραλληλισμό των ευθειών, μπορεί να δείξει ότι οι αντίστοιχες γωνίες είναι ίσες ή να αποδείξει το γεγονός ότι δύο δεδομένες ευθείες είναι κάθετες στην τρίτη κ.λπ. Αλλά σημειώστε ότι είναι συχνά πιο βολικό να χρησιμοποιήσετε τη μέθοδο συντεταγμένων για να αποδείξετε τον παραλληλισμό των γραμμών σε ένα επίπεδο ή σε τρισδιάστατο χώρο.
Παραλληλισμός ευθειών σε ορθογώνιο σύστημα συντεταγμένων
Σε ένα δεδομένο ορθογώνιο σύστημα συντεταγμένων, μια ευθεία γραμμή καθορίζεται από την εξίσωση μιας ευθείας γραμμής σε ένα επίπεδο ενός από τους πιθανούς τύπους. Ομοίως, μια ευθεία γραμμή που ορίζεται σε ένα ορθογώνιο σύστημα συντεταγμένων σε τρισδιάστατο χώρο αντιστοιχεί σε ορισμένες εξισώσεις για μια ευθεία γραμμή στο χώρο.
Ας γράψουμε τις απαραίτητες και επαρκείς συνθήκες για τον παραλληλισμό των ευθειών σε ένα ορθογώνιο σύστημα συντεταγμένων ανάλογα με τον τύπο της εξίσωσης που περιγράφει τις δεδομένες ευθείες.
Ας ξεκινήσουμε με την συνθήκη του παραλληλισμού των ευθειών σε ένα επίπεδο. Βασίζεται στους ορισμούς του διανύσματος κατεύθυνσης μιας ευθείας και του κανονικού διανύσματος μιας ευθείας σε ένα επίπεδο.
Θεώρημα 7
Για να είναι δύο μη συμπίπτουσες γραμμές παράλληλες σε ένα επίπεδο, είναι απαραίτητο και αρκετό τα διανύσματα κατεύθυνσης των δεδομένων γραμμών να είναι συγγραμμικά ή τα κανονικά διανύσματα των δεδομένων γραμμών να είναι συγγραμμικά ή το διάνυσμα κατεύθυνσης μιας ευθείας να είναι κάθετο προς το κανονικό διάνυσμα της άλλης γραμμής.
Γίνεται προφανές ότι η συνθήκη παραλληλισμού ευθειών σε ένα επίπεδο βασίζεται στην συνθήκη της συγγραμμικότητας των διανυσμάτων ή στην συνθήκη της καθετότητας δύο διανυσμάτων. Δηλαδή, αν a → = (a x , a y) και b → = (b x , b y) είναι διανύσματα κατεύθυνσης των ευθειών a και b ;
και n b → = (n b x , n b y) είναι κανονικά διανύσματα των γραμμών a και b, τότε γράφουμε την παραπάνω αναγκαία και επαρκή συνθήκη ως εξής: a → = t · b → ⇔ a x = t · b x a y = t · b y ή n a → = t · n b → ⇔ n a x = t · n b x n a y = t · n b y ή a → , n b → = 0 ⇔ a x · n b x + a y · n b y = 0 , όπου t είναι κάποιος πραγματικός αριθμός. Οι συντεταγμένες των οδηγών ή των ευθειών διανυσμάτων καθορίζονται από τις δεδομένες εξισώσεις των ευθειών. Ας δούμε τα κύρια παραδείγματα.
- Η ευθεία α σε ένα ορθογώνιο σύστημα συντεταγμένων καθορίζεται από τη γενική εξίσωση της ευθείας: A 1 x + B 1 y + C 1 = 0; ευθεία b - A 2 x + B 2 y + C 2 = 0. Τότε τα κανονικά διανύσματα των δεδομένων ευθειών θα έχουν συντεταγμένες (A 1, B 1) και (A 2, B 2), αντίστοιχα. Γράφουμε την συνθήκη παραλληλισμού ως εξής:
A 1 = t A 2 B 1 = t B 2
- Η ευθεία α περιγράφεται από την εξίσωση μιας ευθείας με κλίση της μορφής y = k 1 x + b 1 . Ευθεία b - y = k 2 x + b 2. Τότε τα κανονικά διανύσματα των δεδομένων ευθειών θα έχουν συντεταγμένες (k 1, - 1) και (k 2, - 1), αντίστοιχα, και θα γράψουμε τη συνθήκη παραλληλισμού ως εξής:
k 1 = t k 2 - 1 = t (- 1) ⇔ k 1 = t k 2 t = 1 ⇔ k 1 = k 2
Έτσι, εάν οι παράλληλες ευθείες σε ένα επίπεδο σε ένα ορθογώνιο σύστημα συντεταγμένων δίνονται με εξισώσεις με γωνιακούς συντελεστές, τότε οι γωνιακοί συντελεστές των δεδομένων ευθειών θα είναι ίσοι. Και ισχύει η αντίθετη πρόταση: εάν οι μη συμπίπτουσες γραμμές σε ένα επίπεδο σε ένα ορθογώνιο σύστημα συντεταγμένων καθορίζονται από τις εξισώσεις μιας ευθείας με ίδιους γωνιακούς συντελεστές, τότε αυτές οι δεδομένες ευθείες είναι παράλληλες.
- Οι ευθείες a και b σε ένα ορθογώνιο σύστημα συντεταγμένων προσδιορίζονται από τις κανονικές εξισώσεις μιας ευθείας σε ένα επίπεδο: x - x 1 a x = y - y 1 a y και x - x 2 b x = y - y 2 b y ή από παραμετρικές εξισώσεις του μια ευθεία σε ένα επίπεδο: x = x 1 + λ · a x y = y 1 + λ · a y και x = x 2 + λ · b x y = y 2 + λ · b y .
Τότε τα διανύσματα κατεύθυνσης των δεδομένων ευθειών θα είναι: a x, a y και b x, b y, αντίστοιχα, και θα γράψουμε τη συνθήκη παραλληλισμού ως εξής:
a x = t b x a y = t b y
Ας δούμε παραδείγματα.
Παράδειγμα 1
Δίνονται δύο γραμμές: 2 x - 3 y + 1 = 0 και x 1 2 + y 5 = 1. Είναι απαραίτητο να προσδιοριστεί εάν είναι παράλληλες.
Λύση
Ας γράψουμε την εξίσωση μιας ευθείας σε τμήματα με τη μορφή μιας γενικής εξίσωσης:
x 1 2 + y 5 = 1 ⇔ 2 x + 1 5 y - 1 = 0
Βλέπουμε ότι n a → = (2, - 3) είναι το κανονικό διάνυσμα της ευθείας 2 x - 3 y + 1 = 0, και n b → = 2, 1 5 είναι το κανονικό διάνυσμα της ευθείας x 1 2 + y 5 = 1.
Τα διανύσματα που προκύπτουν δεν είναι συγγραμμικά, γιατί δεν υπάρχει τέτοια τιμή tat που να ισχύει η ισότητα:
2 = t 2 - 3 = t 1 5 ⇔ t = 1 - 3 = t 1 5 ⇔ t = 1 - 3 = 1 5
Έτσι, δεν ικανοποιείται η απαραίτητη και επαρκής προϋπόθεση για τον παραλληλισμό των γραμμών σε ένα επίπεδο, πράγμα που σημαίνει ότι οι δεδομένες ευθείες δεν είναι παράλληλες.
Απάντηση:οι δεδομένες γραμμές δεν είναι παράλληλες.
Παράδειγμα 2
Δίνονται οι ευθείες y = 2 x + 1 και x 1 = y - 4 2. Είναι παράλληλοι;
Λύση
Ας μετατρέψουμε την κανονική εξίσωση της ευθείας x 1 = y - 4 2 στην εξίσωση της ευθείας με την κλίση:
x 1 = y - 4 2 ⇔ 1 · (y - 4) = 2 x ⇔ y = 2 x + 4
Βλέπουμε ότι οι εξισώσεις των ευθειών y = 2 x + 1 και y = 2 x + 4 δεν είναι ίδιες (αν ήταν διαφορετικά, οι ευθείες θα συμπίπτουν) και οι γωνιακοί συντελεστές των ευθειών είναι ίσοι, που σημαίνει ότι οι δεδομένες γραμμές είναι παράλληλες.
Ας προσπαθήσουμε να λύσουμε το πρόβλημα διαφορετικά. Αρχικά, ας ελέγξουμε αν οι γραμμές που δίνονται συμπίπτουν. Χρησιμοποιούμε οποιοδήποτε σημείο της ευθείας y = 2 x + 1, για παράδειγμα, (0, 1), οι συντεταγμένες αυτού του σημείου δεν αντιστοιχούν στην εξίσωση της ευθείας x 1 = y - 4 2, που σημαίνει ότι οι ευθείες κάνουν δεν συμπίπτουν.
Το επόμενο βήμα είναι να προσδιοριστεί εάν πληρούται η συνθήκη παραλληλισμού των δεδομένων ευθειών.
Το κανονικό διάνυσμα της ευθείας y = 2 x + 1 είναι το διάνυσμα n a → = (2 , - 1) , και το διάνυσμα κατεύθυνσης της δεύτερης δεδομένης ευθείας είναι b → = (1 , 2) . Το κλιμακωτό γινόμενο αυτών των διανυσμάτων είναι ίσο με μηδέν:
n a → , b → = 2 1 + (- 1) 2 = 0
Έτσι, τα διανύσματα είναι κάθετα: αυτό μας δείχνει την εκπλήρωση της απαραίτητης και ικανής συνθήκης για τον παραλληλισμό των αρχικών γραμμών. Εκείνοι. οι ευθείες που δίνονται είναι παράλληλες.
Απάντηση:αυτές οι γραμμές είναι παράλληλες.
Για να αποδειχθεί ο παραλληλισμός των γραμμών σε ένα ορθογώνιο σύστημα συντεταγμένων τρισδιάστατου χώρου χρησιμοποιείται η παρακάτω απαραίτητη και επαρκής συνθήκη.
Θεώρημα 8
Για να είναι παράλληλες δύο μη συμπίπτουσες γραμμές στον τρισδιάστατο χώρο, είναι απαραίτητο και αρκετό τα διανύσματα κατεύθυνσης αυτών των γραμμών να είναι συγγραμμικά.
Εκείνοι. Δεδομένων των εξισώσεων των γραμμών στον τρισδιάστατο χώρο, η απάντηση στο ερώτημα: είναι παράλληλες ή όχι, βρίσκεται με τον προσδιορισμό των συντεταγμένων των διανυσμάτων κατεύθυνσης των δεδομένων γραμμών, καθώς και με τον έλεγχο της συνθήκης της συγγραμμικότητάς τους. Με άλλα λόγια, αν a → = (a x, a y, a z) και b → = (b x, b y, b z) είναι τα διανύσματα κατεύθυνσης των ευθειών a και b αντίστοιχα, τότε για να είναι παράλληλες, η ύπαρξη ενός τέτοιου πραγματικού αριθμού t είναι απαραίτητο, ώστε να ισχύει η ισότητα:
a → = t b → ⇔ a x = t b x a y = t b y a z = t b z
Παράδειγμα 3
Δίνονται οι ευθείες x 1 = y - 2 0 = z + 1 - 3 και x = 2 + 2 λ y = 1 z = - 3 - 6 λ. Είναι απαραίτητο να αποδειχθεί ο παραλληλισμός αυτών των γραμμών.
Λύση
Οι συνθήκες του προβλήματος δίνονται από τις κανονικές εξισώσεις μιας ευθείας στο χώρο και τις παραμετρικές εξισώσεις μιας άλλης ευθείας στο χώρο. Διανύσματα οδηγών α → και b → οι δεδομένες ευθείες έχουν συντεταγμένες: (1, 0, - 3) και (2, 0, - 6).
1 = t · 2 0 = t · 0 - 3 = t · - 6 ⇔ t = 1 2 , μετά a → = 1 2 · b → .
Κατά συνέπεια, ικανοποιείται η απαραίτητη και επαρκής συνθήκη για τον παραλληλισμό των γραμμών στο χώρο.
Απάντηση:αποδεικνύεται ο παραλληλισμός των δοσμένων ευθειών.
Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter
ΚΕΦΑΛΑΙΟ III.
ΠΑΡΑΛΛΗΛΟΣ ΑΜΕΣΗ
§ 38. ΕΞΑΡΤΗΣΗ ΜΕΤΑΞΥ ΓΩΝΙΩΝ,
ΣΧΗΜΑΤΙΖΟΝΤΑΙ ΑΠΟ ΔΥΟ ΠΑΡΑΛΛΗΛΕΣ ΓΡΑΜΜΕΣ ΚΑΙ ΜΙΑ ΔΕΥΤΕΡΕΥΟΥΣΑ.
Γνωρίζουμε ότι δύο ευθείες είναι παράλληλες εάν, όταν τέμνουν μια τρίτη ευθεία, οι αντίστοιχες γωνίες είναι ίσες ή οι εσωτερικές ή εξωτερικές γωνίες που βρίσκονται εγκάρσια είναι ίσες, ή το άθροισμα των εσωτερικών ή το άθροισμα των εξωτερικών γωνιών μονής όψης είναι ίσο με 2 ρε. Ας αποδείξουμε ότι αληθεύουν και τα αντίστροφα θεωρήματα, δηλαδή:
Εάν δύο παράλληλες ευθείες διασχίζονται από μια τρίτη, τότε:
1) οι αντίστοιχες γωνίες είναι ίσες.
2) οι εσωτερικές εγκάρσιες γωνίες είναι ίσες.
3) οι εξωτερικές εγκάρσιες γωνίες είναι ίσες.
4) το άθροισμα των εσωτερικών μονόπλευρων γωνιών είναι ίσο με 2
ρε
;
5) το άθροισμα των εξωτερικών μονόπλευρων γωνιών είναι ίσο με 2
ρε
.
Ας αποδείξουμε, για παράδειγμα, ότι αν δύο παράλληλες ευθείες τέμνονται από μια τρίτη ευθεία, τότε οι αντίστοιχες γωνίες είναι ίσες.
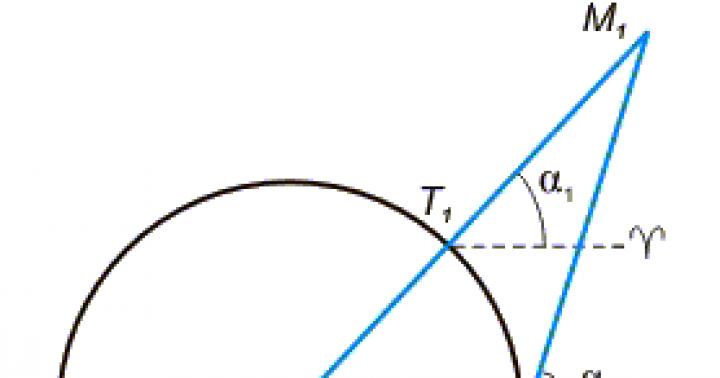
Έστω παράλληλες οι ευθείες ΑΒ και ΓΔ και η τομή τους ΜΝ (Εικ. 202) Ας αποδείξουμε ότι οι αντίστοιχες γωνίες 1 και 2 είναι ίσες μεταξύ τους.
Ας υποθέσουμε ότι / 1 και / 2 δεν είναι ίσα. Τότε στο σημείο Ο μπορούμε να κατασκευάσουμε / ΔΟΕ, αντίστοιχη και ισότιμη / 2 (σχέδιο 203).
Αλλα αν / MOQ = / 2, τότε η ευθεία γραμμή ΟΚ θα είναι παράλληλη με το CD (§ 35).
Βρήκαμε ότι δύο ευθείες γραμμές ΑΒ και ΟΚ σχεδιάστηκαν μέσω του σημείου Ο, παράλληλες στην ευθεία γραμμή CD. Αλλά αυτό δεν μπορεί να είναι (§ 37).
Φτάσαμε σε μια αντίφαση γιατί το υποθέσαμε / 1 και / 2 δεν είναι ίσα. Επομένως, η υπόθεση μας είναι εσφαλμένη και / 1 πρέπει να είναι ίσο / 2, δηλαδή οι αντίστοιχες γωνίες είναι ίσες.
Ας καθορίσουμε τις σχέσεις μεταξύ των υπόλοιπων γωνιών. Έστω οι ευθείες AB και CD να είναι παράλληλες και MN η τομή τους (Εικ. 204).
Μόλις αποδείξαμε ότι στην περίπτωση αυτή οι αντίστοιχες γωνίες είναι ίσες. Ας υποθέσουμε ότι δύο από αυτά έχουν 119° το καθένα. Ας υπολογίσουμε το μέγεθος καθεμιάς από τις άλλες έξι γωνίες. Με βάση τις ιδιότητες γειτονικών και κάθετων γωνιών, διαπιστώνουμε ότι τέσσερις από τις οκτώ γωνίες θα έχουν 119° η καθεμία και οι υπόλοιπες 61° η καθεμία.
Αποδείχθηκε ότι τόσο οι εσωτερικές όσο και οι εξωτερικές εγκάρσιες γωνίες είναι ίσες σε ζεύγη και το άθροισμα των εσωτερικών ή εξωτερικών γωνιών μονής όψης είναι ίσο με 180° (ή 2 ρε).
Το ίδιο θα συμβεί και για οποιαδήποτε άλλη τιμή ίσων αντίστοιχων γωνιών.
Συμπέρασμα 1. Εάν καθεμία από τις δύο ευθείες AB και CD είναι παράλληλη στην ίδια τρίτη γραμμή MN, τότε οι δύο πρώτες ευθείες είναι παράλληλες μεταξύ τους (σχέδιο 205).
Στην πραγματικότητα, σχεδιάζοντας τη διατομή EF (Εικ. 206), παίρνουμε:
ΕΝΑ) /
1 = /
3, αφού ΑΒ || MN; σι) /
2 = /
3, αφού CO || MN.
Που σημαίνει, / 1 = / 2, και αυτές είναι οι γωνίες που αντιστοιχούν στις ευθείες AB και CD και στην τέμνουσα EF, επομένως, οι ευθείες AB και CD είναι παράλληλες.
Συμπέρασμα 2. Εάν μια ευθεία είναι κάθετη σε μία από τις δύο παράλληλες ευθείες, τότε είναι κάθετη και στην άλλη (σχέδιο 207).
Πράγματι, αν EF _|_ AB, τότε / 1 = ρε; αν ΑΒ || CD, λοιπόν / 1 = / 2.
Ως εκ τούτου, / 2 = ρεδηλ. EF _|_ CD .
Αυτό το άρθρο αφορά παράλληλες και παράλληλες ευθείες. Αρχικά, δίνεται ο ορισμός των παράλληλων ευθειών σε επίπεδο και στο διάστημα, εισάγονται σημειώσεις, δίνονται παραδείγματα και γραφικές απεικονίσεις παράλληλων ευθειών. Στη συνέχεια, συζητούνται τα σημάδια και οι προϋποθέσεις για τον παραλληλισμό των ευθειών. Συμπερασματικά, παρουσιάζονται λύσεις σε τυπικά προβλήματα απόδειξης παραλληλισμού ευθειών, οι οποίες δίνονται από ορισμένες εξισώσεις μιας ευθείας σε ένα ορθογώνιο σύστημα συντεταγμένων σε ένα επίπεδο και σε τρισδιάστατο χώρο.
Πλοήγηση στη σελίδα.
Παράλληλες γραμμές - βασικές πληροφορίες.
Ορισμός.
Δύο γραμμές σε ένα επίπεδο ονομάζονται παράλληλο, αν δεν έχουν κοινά σημεία.
Ορισμός.
Δύο γραμμές σε τρισδιάστατο χώρο ονομάζονται παράλληλο, αν βρίσκονται στο ίδιο επίπεδο και δεν έχουν κοινά σημεία.
Σημειώστε ότι η ρήτρα "αν βρίσκονται στο ίδιο επίπεδο" στον ορισμό των παράλληλων ευθειών στο διάστημα είναι πολύ σημαντική. Ας διευκρινίσουμε αυτό το σημείο: δύο ευθείες στον τρισδιάστατο χώρο που δεν έχουν κοινά σημεία και δεν βρίσκονται στο ίδιο επίπεδο δεν είναι παράλληλες, αλλά τέμνουσες.
Ακολουθούν μερικά παραδείγματα παράλληλων ευθειών. Οι απέναντι άκρες του φύλλου σημειωματάριου βρίσκονται σε παράλληλες γραμμές. Οι ευθείες γραμμές κατά τις οποίες το επίπεδο του τοίχου του σπιτιού τέμνει τα επίπεδα της οροφής και του δαπέδου είναι παράλληλες. Οι σιδηροτροχιές σε επίπεδο έδαφος μπορούν επίσης να θεωρηθούν ως παράλληλες γραμμές.
Για να δηλώσετε παράλληλες γραμμές, χρησιμοποιήστε το σύμβολο "". Δηλαδή, αν οι ευθείες a και b είναι παράλληλες, τότε μπορούμε να γράψουμε εν συντομία a b.
Παρακαλώ σημειώστε: εάν οι ευθείες a και b είναι παράλληλες, τότε μπορούμε να πούμε ότι η ευθεία a είναι παράλληλη στην ευθεία b και επίσης ότι η ευθεία b είναι παράλληλη στην ευθεία a.
Ας εκφράσουμε μια δήλωση που παίζει σημαντικό ρόλο στη μελέτη των παράλληλων ευθειών σε ένα επίπεδο: μέσα από ένα σημείο που δεν βρίσκεται σε μια δεδομένη ευθεία, διέρχεται η μόνη ευθεία παράλληλη προς τη δεδομένη. Αυτή η δήλωση γίνεται αποδεκτή ως γεγονός (δεν μπορεί να αποδειχθεί με βάση τα γνωστά αξιώματα της επιπεδομετρίας) και ονομάζεται αξίωμα παράλληλων ευθειών.
Για την περίπτωση στο χώρο, ισχύει το θεώρημα: από οποιοδήποτε σημείο του χώρου που δεν βρίσκεται σε μια δεδομένη ευθεία, διέρχεται μια ευθεία παράλληλη προς τη δεδομένη. Αυτό το θεώρημα αποδεικνύεται εύκολα χρησιμοποιώντας το παραπάνω αξίωμα των παράλληλων ευθειών (μπορείτε να βρείτε την απόδειξή του στο εγχειρίδιο γεωμετρίας για τις τάξεις 10-11, το οποίο παρατίθεται στο τέλος του άρθρου στη λίστα αναφορών).
Για την περίπτωση στο χώρο, ισχύει το θεώρημα: από οποιοδήποτε σημείο του χώρου που δεν βρίσκεται σε μια δεδομένη ευθεία, διέρχεται μια ευθεία παράλληλη προς τη δεδομένη. Αυτό το θεώρημα μπορεί εύκολα να αποδειχθεί χρησιμοποιώντας το παραπάνω αξίωμα της παράλληλης γραμμής.
Παραλληλισμός ευθειών - σημεία και προϋποθέσεις παραλληλισμού.
Σημάδι παραλληλισμού γραμμώνείναι επαρκής προϋπόθεση για να είναι παράλληλες οι ευθείες, δηλαδή προϋπόθεση η εκπλήρωση της οποίας εγγυάται ότι οι ευθείες είναι παράλληλες. Με άλλα λόγια, η εκπλήρωση αυτής της προϋπόθεσης αρκεί για να διαπιστωθεί το γεγονός ότι οι ευθείες είναι παράλληλες.
Υπάρχουν επίσης αναγκαίες και επαρκείς προϋποθέσεις για τον παραλληλισμό των γραμμών σε επίπεδο και σε τρισδιάστατο χώρο.
Ας εξηγήσουμε την έννοια της φράσης «απαραίτητη και επαρκής συνθήκη για παράλληλες ευθείες».
Έχουμε ήδη ασχοληθεί με την επαρκή συνθήκη για παράλληλες γραμμές. Ποια είναι η «απαραίτητη προϋπόθεση για παράλληλες ευθείες»; Από το όνομα "απαραίτητο" είναι σαφές ότι η εκπλήρωση αυτής της προϋπόθεσης είναι απαραίτητη για παράλληλες γραμμές. Με άλλα λόγια, εάν δεν πληρούται η απαραίτητη προϋπόθεση για να είναι παράλληλες οι ευθείες, τότε οι ευθείες δεν είναι παράλληλες. Ετσι, απαραίτητη και επαρκής συνθήκη για παράλληλες γραμμέςείναι μια προϋπόθεση η εκπλήρωση της οποίας είναι και απαραίτητη και επαρκής για παράλληλες ευθείες. Δηλαδή, αφενός, αυτό είναι σημάδι παραλληλισμού ευθειών και αφετέρου, αυτό είναι μια ιδιότητα που έχουν οι παράλληλες ευθείες.
Πριν διατυπώσετε μια απαραίτητη και επαρκή συνθήκη για τον παραλληλισμό των γραμμών, καλό είναι να υπενθυμίσουμε αρκετούς βοηθητικούς ορισμούς.
Τέμνουσα γραμμήείναι μια ευθεία που τέμνει καθεμία από δύο δεδομένες μη συμπίπτουσες ευθείες.
Όταν δύο ευθείες τέμνονται με ένα εγκάρσιο, σχηματίζονται οκτώ μη ανεπτυγμένες. Στη διατύπωση της αναγκαίας και ικανής συνθήκης για τον παραλληλισμό των ευθειών, τα λεγόμενα ξαπλωμένος σταυρωτά, αντίστοιχοςΚαι μονόπλευρες γωνίες. Ας τα δείξουμε στο σχέδιο.
Θεώρημα.
Εάν δύο ευθείες σε ένα επίπεδο τέμνονται από ένα εγκάρσιο, τότε για να είναι παράλληλες είναι απαραίτητο και αρκετό οι τέμνουσες γωνίες να είναι ίσες ή οι αντίστοιχες γωνίες να είναι ίσες ή το άθροισμα των μονόπλευρων γωνιών να είναι ίσο με 180 βαθμούς.
Ας δείξουμε μια γραφική απεικόνιση αυτής της απαραίτητης και ικανής συνθήκης για τον παραλληλισμό των γραμμών σε ένα επίπεδο.
Μπορείτε να βρείτε αποδείξεις αυτών των συνθηκών για τον παραλληλισμό των γραμμών σε εγχειρίδια γεωμετρίας για τις τάξεις 7-9.
Σημειώστε ότι αυτές οι συνθήκες μπορούν επίσης να χρησιμοποιηθούν σε τρισδιάστατο χώρο - το κύριο πράγμα είναι ότι οι δύο ευθείες γραμμές και η τομή βρίσκονται στο ίδιο επίπεδο.
Ακολουθούν μερικά ακόμη θεωρήματα που χρησιμοποιούνται συχνά για να αποδείξουν τον παραλληλισμό των ευθειών.
Θεώρημα.
Εάν δύο ευθείες σε ένα επίπεδο είναι παράλληλες με μια τρίτη γραμμή, τότε είναι παράλληλες. Η απόδειξη αυτού του κριτηρίου προκύπτει από το αξίωμα των παράλληλων ευθειών.
Υπάρχει παρόμοια συνθήκη για παράλληλες γραμμές στον τρισδιάστατο χώρο.
Θεώρημα.
Αν δύο ευθείες στο διάστημα είναι παράλληλες με μια τρίτη γραμμή, τότε είναι παράλληλες. Η απόδειξη αυτού του κριτηρίου συζητείται στα μαθήματα γεωμετρίας στη 10η τάξη.
Ας επεξηγήσουμε τα θεωρήματα που αναφέρθηκαν.
Ας παρουσιάσουμε ένα άλλο θεώρημα που μας επιτρέπει να αποδείξουμε τον παραλληλισμό των ευθειών σε ένα επίπεδο.
Θεώρημα.
Αν δύο ευθείες σε ένα επίπεδο είναι κάθετες σε μια τρίτη γραμμή, τότε είναι παράλληλες.
Υπάρχει ένα παρόμοιο θεώρημα για τις ευθείες στο διάστημα.
Θεώρημα.
Αν δύο ευθείες στον τρισδιάστατο χώρο είναι κάθετες στο ίδιο επίπεδο, τότε είναι παράλληλες.
Ας σχεδιάσουμε εικόνες που αντιστοιχούν σε αυτά τα θεωρήματα.
Όλα τα θεωρήματα, τα κριτήρια και οι απαραίτητες και επαρκείς συνθήκες που διατυπώθηκαν παραπάνω είναι εξαιρετικά για την απόδειξη του παραλληλισμού των ευθειών χρησιμοποιώντας τις μεθόδους της γεωμετρίας. Δηλαδή, για να αποδείξετε τον παραλληλισμό δύο δεδομένων ευθειών, πρέπει να δείξετε ότι είναι παράλληλες με μια τρίτη γραμμή ή να δείξετε την ισότητα των εγκάρσιων γωνιών κ.λπ. Πολλά παρόμοια προβλήματα λύνονται στα μαθήματα γεωμετρίας στο λύκειο. Ωστόσο, πρέπει να σημειωθεί ότι σε πολλές περιπτώσεις είναι βολικό να χρησιμοποιηθεί η μέθοδος συντεταγμένων για να αποδειχθεί ο παραλληλισμός των γραμμών σε ένα επίπεδο ή σε τρισδιάστατο χώρο. Ας διατυπώσουμε τις απαραίτητες και επαρκείς προϋποθέσεις για τον παραλληλισμό των γραμμών που καθορίζονται σε ένα ορθογώνιο σύστημα συντεταγμένων.
Παραλληλισμός ευθειών σε ορθογώνιο σύστημα συντεταγμένων.
Σε αυτή την παράγραφο του άρθρου θα διατυπώσουμε απαραίτητες και επαρκείς προϋποθέσεις για παράλληλες γραμμέςσε ένα ορθογώνιο σύστημα συντεταγμένων, ανάλογα με τον τύπο των εξισώσεων που ορίζουν αυτές τις γραμμές, και θα δώσουμε επίσης λεπτομερείς λύσεις σε χαρακτηριστικά προβλήματα.
Ας ξεκινήσουμε με την συνθήκη του παραλληλισμού δύο ευθειών σε ένα επίπεδο στο ορθογώνιο σύστημα συντεταγμένων Oxy. Η απόδειξή του βασίζεται στον ορισμό του διανύσματος κατεύθυνσης μιας ευθείας και στον ορισμό του κανονικού διανύσματος μιας ευθείας σε ένα επίπεδο.
Θεώρημα.
Για να είναι δύο μη συμπίπτουσες ευθείες παράλληλες σε ένα επίπεδο, είναι απαραίτητο και αρκετό τα διανύσματα κατεύθυνσης αυτών των γραμμών να είναι συγγραμμικά ή τα κανονικά διανύσματα αυτών των γραμμών να είναι συγγραμμικά ή το διάνυσμα κατεύθυνσης μιας ευθείας να είναι κάθετο στην κανονική διάνυσμα της δεύτερης γραμμής.
Προφανώς, η συνθήκη παραλληλισμού δύο ευθειών σε ένα επίπεδο μειώνεται σε (διανύσματα κατεύθυνσης ευθειών ή κανονικά διανύσματα ευθειών) ή σε (διάνυσμα κατεύθυνσης μιας ευθείας και κανονικό διάνυσμα της δεύτερης ευθείας). Έτσι, εάν και είναι διανύσματα κατεύθυνσης των ευθειών a και b, και 
Και 
είναι κανονικά διανύσματα των ευθειών a και b αντίστοιχα, τότε η απαραίτητη και επαρκής συνθήκη για τον παραλληλισμό των γραμμών a και b θα γραφεί ως 
, ή 
, ή , όπου t είναι κάποιος πραγματικός αριθμός. Με τη σειρά τους, οι συντεταγμένες των οδηγών και (ή) των κανονικών διανυσμάτων των γραμμών a και b βρίσκονται χρησιμοποιώντας τις γνωστές εξισώσεις των γραμμών.
Συγκεκριμένα, αν η ευθεία γραμμή a στο ορθογώνιο σύστημα συντεταγμένων Oxy στο επίπεδο ορίζει μια γενική ευθεία εξίσωση της μορφής 
και ευθεία γραμμή β - 
, τότε τα κανονικά διανύσματα αυτών των ευθειών έχουν συντεταγμένες και, αντίστοιχα, και η συνθήκη για παραλληλισμό των ευθειών a και b θα γραφεί ως .
Αν η ευθεία a αντιστοιχεί στην εξίσωση μιας ευθείας με γωνιακό συντελεστή της μορφής, και η ευθεία b-, τότε τα κανονικά διανύσματα αυτών των ευθειών έχουν συντεταγμένες και, και η συνθήκη για παραλληλισμό αυτών των ευθειών παίρνει τη μορφή 
. Κατά συνέπεια, εάν οι ευθείες σε ένα επίπεδο σε ένα ορθογώνιο σύστημα συντεταγμένων είναι παράλληλες και μπορούν να προσδιοριστούν με εξισώσεις ευθειών με γωνιακούς συντελεστές, τότε οι γωνιακοί συντελεστές των ευθειών θα είναι ίσοι. Και το αντίστροφο: εάν οι μη συμπίπτουσες γραμμές σε ένα επίπεδο σε ένα ορθογώνιο σύστημα συντεταγμένων μπορούν να προσδιοριστούν με εξισώσεις μιας ευθείας με ίσους γωνιακούς συντελεστές, τότε τέτοιες ευθείες είναι παράλληλες.
Αν μια ευθεία a και μια ευθεία b σε ένα ορθογώνιο σύστημα συντεταγμένων καθορίζονται από τις κανονικές εξισώσεις μιας ευθείας σε ένα επίπεδο της μορφής 
Και 
, ή παραμετρικές εξισώσεις ευθείας σε επίπεδο της μορφής 
Και 
Συνεπώς, τα διανύσματα κατεύθυνσης αυτών των ευθειών έχουν συντεταγμένες και , και η συνθήκη για παραλληλισμό των ευθειών a και b γράφεται ως .
Ας δούμε λύσεις σε πολλά παραδείγματα.
Παράδειγμα.
Οι ευθείες είναι παράλληλες; 
Και ?
Λύση.
Ας ξαναγράψουμε την εξίσωση μιας γραμμής σε τμήματα με τη μορφή μιας γενικής εξίσωσης μιας γραμμής: 
. Τώρα μπορούμε να δούμε ότι είναι το κανονικό διάνυσμα της γραμμής , το a είναι το κανονικό διάνυσμα της ευθείας. Αυτά τα διανύσματα δεν είναι συγγραμμικά, καθώς δεν υπάρχει πραγματικός αριθμός t για τον οποίο η ισότητα ( 
). Συνεπώς, δεν ικανοποιείται η απαραίτητη και επαρκής προϋπόθεση για τον παραλληλισμό ευθειών σε ένα επίπεδο, επομένως οι δεδομένες ευθείες δεν είναι παράλληλες.
Απάντηση:
Όχι, οι γραμμές δεν είναι παράλληλες.
Παράδειγμα.
Είναι οι ευθείες και παράλληλες;
Λύση.
Ας ανάγουμε την κανονική εξίσωση μιας ευθείας στην εξίσωση μιας ευθείας με γωνιακό συντελεστή: . Προφανώς, οι εξισώσεις των ευθειών και δεν είναι ίδιες (σε αυτή την περίπτωση, οι δεδομένες ευθείες θα ήταν ίδιες) και οι γωνιακοί συντελεστές των ευθειών είναι ίσοι, επομένως, οι αρχικές ευθείες είναι παράλληλες.
Σελίδα 1 από 2
Ερώτηση 1.Να αποδείξετε ότι δύο ευθείες παράλληλες σε μια τρίτη είναι παράλληλες.
Απάντηση. Θεώρημα 4.1. Δύο ευθείες παράλληλες σε μια τρίτη είναι παράλληλες.
Απόδειξη.Έστω οι ευθείες a και b παράλληλες με την ευθεία c. Ας υποθέσουμε ότι τα α και β δεν είναι παράλληλα (Εικ. 69). Τότε δεν τέμνονται σε κάποιο σημείο Γ. Αυτό σημαίνει ότι δύο ευθείες διέρχονται από το σημείο Γ παράλληλα με την ευθεία γ. Αλλά αυτό είναι αδύνατο, αφού μέσα από ένα σημείο που δεν βρίσκεται σε μια δεδομένη ευθεία, μπορείτε να σχεδιάσετε το πολύ μία ευθεία παράλληλη προς τη δεδομένη. Το θεώρημα έχει αποδειχθεί.
Ερώτηση 2.Εξηγήστε ποιες γωνίες ονομάζονται μονόπλευρες εσωτερικές γωνίες. Ποιες γωνίες ονομάζονται εσωτερικές εγκάρσιες γωνίες;
Απάντηση.Τα ζεύγη γωνιών που σχηματίζονται όταν οι γραμμές AB και CD τέμνονται με την τέμνουσα AC έχουν ειδικά ονόματα.
Εάν τα σημεία B και D βρίσκονται στο ίδιο ημιεπίπεδο σε σχέση με την ευθεία γραμμή AC, τότε οι γωνίες BAC και DCA ονομάζονται μονόπλευρες εσωτερικές γωνίες (Εικ. 71, α).
Εάν τα σημεία B και D βρίσκονται σε διαφορετικά ημιεπίπεδα σε σχέση με την ευθεία γραμμή AC, τότε οι γωνίες BAC και DCA ονομάζονται εσωτερικές εγκάρσιες γωνίες (Εικ. 71, β).
Ρύζι. 71
Ερώτηση 3.Αποδείξτε ότι αν οι εσωτερικές γωνίες ενός ζεύγους είναι ίσες, τότε οι εσωτερικές γωνίες του άλλου ζεύγους είναι επίσης ίσες και το άθροισμα των εσωτερικών γωνιών κάθε ζεύγους είναι 180°.
Απάντηση.Το τέμνον AC σχηματίζει με τις ευθείες γραμμές AB και CD δύο ζεύγη εσωτερικών μονόπλευρων γωνιών και δύο ζεύγη εσωτερικών εγκάρσιων γωνιών. Οι εσωτερικές εγκάρσιες γωνίες ενός ζεύγους, για παράδειγμα η γωνία 1 και η γωνία 2, γειτνιάζουν με τις εσωτερικές εγκάρσιες γωνίες ενός άλλου ζεύγους: γωνία 3 και γωνία 4 (Εικ. 72).
Ρύζι. 72
Επομένως, εάν οι εσωτερικές γωνίες ενός ζεύγους είναι ίσες, τότε οι εσωτερικές γωνίες του άλλου ζεύγους είναι επίσης ίσες.
Ένα ζεύγος εσωτερικών εγκάρσιων γωνιών, για παράδειγμα γωνία 1 και γωνία 2, και ένα ζεύγος εσωτερικών γωνιών μονής όψης, για παράδειγμα γωνία 2 και γωνία 3, έχουν μία κοινή γωνία - γωνία 2, και δύο άλλες γωνίες είναι γειτονικές : γωνία 1 και γωνία 3.
Επομένως, εάν οι εσωτερικές εγκάρσιες γωνίες είναι ίσες, τότε το άθροισμα των εσωτερικών γωνιών είναι 180°. Και αντίστροφα: αν το άθροισμα των εσωτερικών τεμνόμενων γωνιών είναι ίσο με 180°, τότε οι τεμνόμενες εσωτερικές γωνίες είναι ίσες. Q.E.D.
Ερώτηση 4.Αποδείξτε μια δοκιμή για παράλληλες ευθείες.
Απάντηση. Θεώρημα 4.2 (δοκιμή για παράλληλες ευθείες).Εάν οι εσωτερικές εγκάρσιες γωνίες είναι ίσες ή το άθροισμα των εσωτερικών μονόπλευρων γωνιών είναι ίσο με 180°, τότε οι ευθείες είναι παράλληλες.
Απόδειξη.Αφήστε τις ευθείες α και β να σχηματίσουν ίσες εσωτερικές εγκάρσιες γωνίες με την τέμνουσα ΑΒ (Εικ. 73, α). Ας πούμε ότι οι ευθείες a και b δεν είναι παράλληλες, που σημαίνει ότι τέμνονται σε κάποιο σημείο C (Εικ. 73, β).
Ρύζι. 73
Η τέμνουσα ΑΒ διαιρεί το επίπεδο σε δύο ημιεπίπεδα. Σε ένα από αυτά βρίσκεται το σημείο C. Ας κατασκευάσουμε ένα τρίγωνο BAC 1, ίσο με το τρίγωνο ABC, με κορυφή C 1 σε άλλο ημιεπίπεδο. Κατά συνθήκη, οι εσωτερικές εγκάρσιες γωνίες για την παράλληλη a, b και την τέμνουσα ΑΒ είναι ίσες. Εφόσον οι αντίστοιχες γωνίες των τριγώνων ABC και BAC 1 με κορυφές Α και Β είναι ίσες, συμπίπτουν με τις εσωτερικές γωνίες που βρίσκονται εγκάρσια. Αυτό σημαίνει ότι η ευθεία AC 1 συμπίπτει με την ευθεία a και η ευθεία BC 1 συμπίπτει με τη γραμμή b. Αποδεικνύεται ότι δύο διαφορετικές ευθείες γραμμές a και b διέρχονται από τα σημεία C και C 1. Και αυτό είναι αδύνατο. Αυτό σημαίνει ότι οι ευθείες a και b είναι παράλληλες.
Αν οι ευθείες α και β και το εγκάρσιο ΑΒ έχουν το άθροισμα των εσωτερικών γωνιών μονής όψης ίσο με 180°, τότε, όπως γνωρίζουμε, οι εσωτερικές γωνίες που βρίσκονται εγκάρσια είναι ίσες. Αυτό σημαίνει, σύμφωνα με όσα αποδείχθηκαν παραπάνω, οι ευθείες α και β είναι παράλληλες. Το θεώρημα έχει αποδειχθεί.
Ερώτηση 5.Εξηγήστε ποιες γωνίες ονομάζονται αντίστοιχες γωνίες. Να αποδείξετε ότι αν οι εσωτερικές εγκάρσιες γωνίες είναι ίσες, τότε και οι αντίστοιχες γωνίες είναι ίσες και αντίστροφα.
Απάντηση.Αν για ένα ζεύγος εσωτερικών εγκάρσιων γωνιών μια γωνία αντικατασταθεί από μια κατακόρυφη, τότε παίρνουμε ένα ζεύγος γωνιών που ονομάζονται αντίστοιχες γωνίες αυτών των ευθειών με εγκάρσια. Αυτό που έπρεπε να εξηγηθεί.
Από την ισότητα των εσωτερικών γωνιών που βρίσκονται σταυρωτά προκύπτει η ισότητα των αντίστοιχων γωνιών και αντίστροφα. Ας υποθέσουμε ότι έχουμε δύο παράλληλες ευθείες (αφού κατά συνθήκη, οι εσωτερικές γωνίες που βρίσκονται η μία απέναντι από την άλλη είναι ίσες) και μια εγκάρσια, που σχηματίζουν τις γωνίες 1, 2, 3. Οι γωνίες 1 και 2 είναι ίσες με τις εσωτερικές γωνίες που βρίσκονται μεταξύ τους. Και οι γωνίες 2 και 3 είναι ίσες ως κατακόρυφες. Παίρνουμε: \(\γωνία\)1 = \(\γωνία\)2 και \(\γωνία\)2 = \(\γωνία\)3. Από την ιδιότητα της μεταβατικότητας του πρόσημου ίσου προκύπτει ότι \(\γωνία\)1 = \(\γωνία\)3. Η αντίστροφη δήλωση μπορεί να αποδειχθεί με παρόμοιο τρόπο.
Από αυτό παίρνουμε το πρόσημο ότι οι ευθείες γραμμές είναι παράλληλες στις αντίστοιχες γωνίες. Δηλαδή: οι ευθείες είναι παράλληλες αν οι αντίστοιχες γωνίες είναι ίσες. Q.E.D.
Ερώτηση 6.Αποδείξτε ότι μέσα από ένα σημείο που δεν βρίσκεται σε μια δεδομένη ευθεία μπορείτε να σχεδιάσετε μια γραμμή παράλληλη με αυτό. Πόσες ευθείες παράλληλες σε μια δεδομένη ευθεία μπορούν να συρθούν μέσα από ένα σημείο που δεν βρίσκεται σε αυτήν την ευθεία;
Απάντηση.Πρόβλημα (8). Δίνεται μια ευθεία ΑΒ και ένα σημείο Γ που δεν βρίσκεται σε αυτή την ευθεία. Αποδείξτε ότι μέσω του σημείου Γ μπορείτε να σχεδιάσετε μια ευθεία παράλληλη στην ευθεία ΑΒ.
Λύση. Η γραμμή AC διαιρεί το επίπεδο σε δύο ημιεπίπεδα (Εικ. 75). Το σημείο Β βρίσκεται σε ένα από αυτά. Ας προσθέσουμε γωνία ACD από την ημιευθεία CA σε ένα άλλο ημιεπίπεδο, ίσο με τη γωνία CAB. Τότε οι ευθείες AB και CD θα είναι παράλληλες. Στην πραγματικότητα, για αυτές τις γραμμές και το τέμνον AC, οι εσωτερικές γωνίες BAC και DCA βρίσκονται σταυρωτά. Και αφού είναι ίσες, οι ευθείες ΑΒ και ΓΔ είναι παράλληλες. Q.E.D.
Συγκρίνοντας τη δήλωση του προβλήματος 8 και του αξιώματος IX (η κύρια ιδιότητα των παράλληλων ευθειών), καταλήγουμε σε ένα σημαντικό συμπέρασμα: μέσω ενός σημείου που δεν βρίσκεται σε μια δεδομένη ευθεία, είναι δυνατό να σχεδιάσουμε μια ευθεία παράλληλη προς αυτήν και μόνο μία.
Ερώτηση 7.Να αποδείξετε ότι αν δύο ευθείες τέμνονται από μια τρίτη γραμμή, τότε οι τεμνόμενες εσωτερικές γωνίες είναι ίσες και το άθροισμα των εσωτερικών μονόπλευρων γωνιών είναι 180°.
Απάντηση. Θεώρημα 4.3(το αντίστροφο του Θεωρήματος 4.2). Εάν δύο παράλληλες ευθείες τέμνονται με μια τρίτη ευθεία, τότε οι τεμνόμενες εσωτερικές γωνίες είναι ίσες και το άθροισμα των εσωτερικών γωνιών μονής όψης είναι 180°.
Απόδειξη.Έστω η a και η b παράλληλες ευθείες και η c μια ευθεία που τις τέμνει στα σημεία A και B. Ας τραβήξουμε μια ευθεία a 1 έως το σημείο A έτσι ώστε οι εσωτερικές εγκάρσιες γωνίες που σχηματίζονται από το εγκάρσιο c με τις ευθείες a 1 και b να είναι ίσες (Εικ. 76).
Σύμφωνα με την αρχή του παραλληλισμού των ευθειών, οι ευθείες a 1 και b είναι παράλληλες. Και εφόσον μόνο μία ευθεία διέρχεται από το σημείο Α, παράλληλη προς την ευθεία b, τότε η ευθεία a συμπίπτει με την ευθεία a 1.
Αυτό σημαίνει ότι οι εσωτερικές εγκάρσιες γωνίες που σχηματίζονται από ένα εγκάρσιο με
οι παράλληλες ευθείες α και β είναι ίσες. Το θεώρημα έχει αποδειχθεί.
Ερώτηση 8.Να αποδείξετε ότι δύο ευθείες κάθετες σε μια τρίτη είναι παράλληλες. Αν μια ευθεία είναι κάθετη σε μία από τις δύο παράλληλες ευθείες, τότε είναι κάθετη και στην άλλη.
Απάντηση.Από το Θεώρημα 4.2 προκύπτει ότι δύο ευθείες κάθετες σε μια τρίτη είναι παράλληλες.
Ας υποθέσουμε ότι οποιεσδήποτε δύο ευθείες είναι κάθετες σε μια τρίτη γραμμή. Αυτό σημαίνει ότι αυτές οι γραμμές τέμνονται με την τρίτη γραμμή υπό γωνία ίση με 90°.
Από την ιδιότητα των γωνιών που σχηματίζονται όταν οι παράλληλες ευθείες τέμνονται με μια εγκάρσια, προκύπτει ότι αν μια ευθεία είναι κάθετη σε μια από τις παράλληλες ευθείες, τότε είναι και κάθετη στην άλλη.
Ερώτηση 9.Να αποδείξετε ότι το άθροισμα των γωνιών ενός τριγώνου είναι 180°.
Απάντηση. Θεώρημα 4.4.Το άθροισμα των γωνιών ενός τριγώνου είναι 180°.
Απόδειξη.Έστω ABC το δοσμένο τρίγωνο. Ας τραβήξουμε μια ευθεία στην κορυφή Β παράλληλη στην ευθεία AC. Ας σημειώσουμε το σημείο D πάνω του έτσι ώστε τα σημεία Α και Δ να βρίσκονται σε αντίθετες πλευρές της ευθείας BC (Εικ. 78).
Οι γωνίες DBC και ACB είναι ίσες ως εσωτερικές εγκάρσιες που σχηματίζονται από το εγκάρσιο BC με παράλληλες γραμμές AC και BD. Επομένως, το άθροισμα των γωνιών ενός τριγώνου στις κορυφές Β και Γ είναι ίσο με τη γωνία ΑΒΔ.
Και το άθροισμα και των τριών γωνιών ενός τριγώνου είναι ίσο με το άθροισμα των γωνιών ABD και BAC. Εφόσον πρόκειται για μονόπλευρες εσωτερικές γωνίες για παράλληλες AC και BD και τέμνουσες AB, το άθροισμά τους είναι 180°. Το θεώρημα έχει αποδειχθεί.
Ερώτηση 10.Να αποδείξετε ότι οποιοδήποτε τρίγωνο έχει τουλάχιστον δύο οξείες γωνίες.
Απάντηση.Πράγματι, ας υποθέσουμε ότι το τρίγωνο έχει μόνο μία οξεία γωνία ή καθόλου οξείες γωνίες. Τότε αυτό το τρίγωνο έχει δύο γωνίες, καθεμία από τις οποίες είναι τουλάχιστον 90°. Το άθροισμα αυτών των δύο γωνιών δεν είναι μικρότερο από 180°. Αυτό όμως είναι αδύνατο, αφού το άθροισμα όλων των γωνιών ενός τριγώνου είναι 180°. Q.E.D.
