Matematica este ceea ceoamenii controlează natura și pe ei înșiși.
Matematicianul sovietic, academicianul A.N. Kolmogorov
Progresie geometrică.
Alături de sarcinile pentru progresii aritmetice, sarcinile legate de conceptul de progresie geometrică sunt, de asemenea, frecvente la testele de admitere la matematică. Pentru a rezolva cu succes astfel de probleme, trebuie să cunoașteți proprietățile unei progresii geometrice și să aveți bune abilități în utilizarea lor.
Acest articol este dedicat prezentării principalelor proprietăți ale unei progresii geometrice. De asemenea, oferă exemple de rezolvare a unor probleme tipice, împrumutat din sarcinile probelor de admitere la matematică.
Să notăm în prealabil principalele proprietăți ale unei progresii geometrice și să amintim cele mai importante formule și enunțuri, asociat cu acest concept.
Definiție. O succesiune numerică se numește progresie geometrică dacă fiecare dintre numerele sale, începând de la al doilea, este egal cu precedentul, înmulțit cu același număr. Numărul se numește numitorul unei progresii geometrice.
Pentru o progresie geometricăformulele sunt valabile
, (1)
Unde . Formula (1) se numește formula termenului general al unei progresii geometrice, iar formula (2) este proprietatea principală a unei progresii geometrice: fiecare membru al progresiei coincide cu media geometrică a membrilor săi vecini și .
Notă, că tocmai din cauza acestei proprietăţi progresia în cauză se numeşte „geometrică”.
Formulele (1) și (2) de mai sus sunt rezumate după cum urmează:
, (3)
Pentru a calcula suma primul membrii unei progresii geometricese aplica formula
Dacă desemnăm
Unde . Deoarece , formula (6) este o generalizare a formulei (5).
În cazul când și progresie geometricăeste în scădere infinită. Pentru a calcula sumadintre toți membrii unei progresii geometrice infinit descrescătoare, se utilizează formula
. (7)
De exemplu , folosind formula (7), se poate arăta, ce
Unde . Aceste egalități se obțin din formula (7) cu condiția ca , (prima egalitate) și , (a doua egalitate).
Teorema. Daca atunci
Dovada. Daca atunci ,
Teorema a fost demonstrată.
Să trecem la luarea în considerare a exemplelor de rezolvare a problemelor pe tema „Progresiune geometrică”.
Exemplul 1 Având în vedere: , și . A găsi .
Decizie. Dacă se aplică formula (5), atunci
Răspuns: .
Exemplul 2 Lasă și . A găsi .
Decizie. Deoarece și , folosim formulele (5), (6) și obținem sistemul de ecuații
Dacă a doua ecuație a sistemului (9) este împărțită la prima, apoi sau . Din aceasta rezultă . Să luăm în considerare două cazuri.
1. Dacă , atunci din prima ecuație a sistemului (9) avem.
2. Dacă , atunci .
Exemplul 3 Să , și . A găsi .
Decizie. Din formula (2) rezultă că sau . De când , atunci sau .
După condiție. Cu toate acestea , prin urmare . Pentru că și, atunci aici avem un sistem de ecuații
Dacă a doua ecuație a sistemului este împărțită la prima, atunci sau .
Deoarece , ecuația are o singură rădăcină adecvată . În acest caz, prima ecuație a sistemului implică .
Ținând cont de formula (7), obținem.
Răspuns: .
Exemplul 4 Având în vedere: și . A găsi .
Decizie. De atunci .
Pentru că, atunci sau
Conform formulei (2), avem . În acest sens, din egalitatea (10) obținem sau .
Cu toate acestea, prin condiție, prin urmare.
Exemplul 5 Se știe că . A găsi .
Decizie. Conform teoremei, avem două egalități
De când , atunci sau . Pentru că atunci .
Răspuns: .
Exemplul 6 Având în vedere: și . A găsi .
Decizie.Ținând cont de formula (5), obținem
De atunci . De când , și , atunci .
Exemplul 7 Lasă și . A găsi .
Decizie. Conform formulei (1), putem scrie
Prin urmare, avem sau . Se știe că și , prin urmare și .
Răspuns: .
Exemplul 8 Aflați numitorul unei progresii geometrice descrescătoare infinite dacă
și .
Decizie. Din formula (7) rezultăși . De aici și din starea problemei, obținem sistemul de ecuații
Dacă prima ecuație a sistemului este la pătrat, și apoi împărțiți ecuația rezultată la a doua ecuație, apoi primim
Sau .
Răspuns: .
Exemplul 9 Găsiți toate valorile pentru care șirul , , este o progresie geometrică.
Decizie. Să , și . Conform formulei (2), care definește proprietatea principală a unei progresii geometrice, putem scrie sau .
De aici obținem ecuația pătratică, ale căror rădăcini suntși .
Să verificăm: dacă, apoi , și ; dacă , atunci , și .
În primul caz avemși , iar în al doilea - și .
Răspuns: , .
Exemplul 10rezolva ecuatia
, (11)
unde si .
Decizie. Partea stângă a ecuației (11) este suma unei progresii geometrice descrescătoare infinite, în care și , cu condiția: și .
Din formula (7) rezultă, ce . În acest sens, ecuația (11) ia forma sau . rădăcină potrivită ecuația pătratică este
Răspuns: .
Exemplul 11. P succesiune de numere pozitiveformează o progresie aritmetică, A - progresie geometrică, ce legatura are cu . A găsi .
Decizie. La fel de succesiune aritmetică, apoi (proprietatea principală a unei progresii aritmetice). În măsura în care, apoi sau . Asta implică , că progresia geometrică este. Conform formulei (2), apoi scriem asta .
De când și , atunci . În acest caz, expresia ia forma sau . După condiție, deci din ecuațieobţinem soluţia unică a problemei luate în considerare, adică .
Răspuns: .
Exemplul 12. Calculați suma
. (12)
Decizie. Înmulțiți ambele părți ale egalității (12) cu 5 și obțineți
Dacă scădem (12) din expresia rezultată, apoi
sau .
Pentru a calcula, înlocuim valorile în formula (7) și obținem . De atunci .
Răspuns: .
Exemplele de rezolvare a problemelor prezentate aici vor fi utile candidaților în pregătirea examenelor de admitere. Pentru un studiu mai profund al metodelor de rezolvare a problemelor, asociat cu o progresie geometrică, puteți folosi tutorialele din lista de literatură recomandată.
1. Culegere de sarcini la matematică pentru solicitanții la universitățile tehnice / Ed. M.I. Scanavi. – M.: Mir i Obrazovanie, 2013. – 608 p.
2. Suprun V.P. Matematică pentru liceeni: secțiuni suplimentare din programa școlară. – M.: Lenand / URSS, 2014. - 216 p.
3. Medynsky M.M. Un curs complet de matematică elementară în sarcini și exerciții. Cartea 2: Secvențe de numere și progresii. – M.: Editus, 2015. - 208 p.
Aveti vreo intrebare?
Pentru a obține ajutorul unui tutore - înregistrați-vă.
site, cu copierea integrală sau parțială a materialului, este necesară un link către sursă.
Lecție aferentă „Progresie geometrică în scădere infinită”
Scopul lecției: introducerea elevilor într-un nou tip de succesiune – o progresie geometrică în scădere infinită.
Sarcini:
formularea ideii inițiale a limitei succesiunii numerice; cunoașterea unui alt mod de conversie a fracțiilor periodice infinite în fracții obișnuite folosind formula pentru suma unei progresii geometrice infinit descrescătoare;
dezvoltarea calităților intelectuale ale personalității școlarilor, cum ar fi gândirea logică, capacitatea de acțiuni evaluative, generalizare;
educaţia activităţii, asistenţa reciprocă, colectivismul, interesul pentru subiect.
Echipament: clasa de calculatoare, proiector, ecran.
Tip de lecție: Lecție - stăpânirea unui subiect nou.
În timpul orelor
eu . Org. moment. Mesaj despre subiectul și scopul lecției.
II . Actualizarea cunoștințelor elevilor.1. Verificarea temelor.
1) Verificarea formulelor de bază referitoare la progresiile aritmetice și geometrice. Doi elevi notează formule la tablă.
2) Restul elevilor o fac dictare matematică pe tema „Formulele sumei”.
Sarcini:
№1. Găsiți suma primilor cinci membri ai unei progresii aritmetice dacă primul său membru este 6 (prima opțiune), -20 (a doua opțiune), iar al cincilea membru este -6 (prima opțiune), 20 (a doua opțiune).
№2. Găsiți suma primilor cinci membri ai unei progresii aritmetice dacă primul ei membru este -20 (prima opțiune), 6 (a doua opțiune), iar diferența este 10 (prima opțiune), -3 (a doua opțiune).
№3. Aflați suma primilor cinci termeni ai unei progresii geometrice dacă primul său termen este 1 (prima opțiune), -1 (a doua opțiune), iar numitorul este -2 (prima opțiune), 2 (a doua opțiune).
La sfârșitul dictatului, selectiv, se verifică lucrările a doi elevi pentru evaluare, restul efectuează autoexaminare după soluții gata făcute scrise pe reverele tablei.
Solutii:

Sarcini
1. Progresia aritmetică este dată de formula A n = 7 – 4 n. Găsi A 10 . (-33)
2. Progresie aritmetică A 3 = 7 și A 5 = 1 . Găsi A 4 . (4)
3. Progresie aritmetică A 3 = 7 și A 5 = 1 . Găsi A 17 . (-35)
4. Progresie aritmetică A 3 = 7 și A 5 = 1 . Găsi S 17 . (-187)
5. Pentru o progresie geometrică  găsiți al cincilea termen.
găsiți al cincilea termen. 
6. Pentru o progresie geometrică  găsi n-al-lea membru.
găsi n-al-lea membru. 
7. Exponenţial b 3 = 8 și b 5 = 2 . Găsi b 4 . (4)
8. Exponenţial b
3
= 8
și b
5
= 2
. Găsi b
1
și
q
. 
9. Exponenţial b 3 = 8 și b 5 = 2 . Găsi S 5 . (62)
III . Explorarea unui subiect nou(prezentare demonstrativă).

Să considerăm un pătrat cu latura egală cu 1. Să desenăm un alt pătrat, a cărui latură este jumătate din primul pătrat, apoi altul, a cărui latură este jumătate din al doilea, apoi următorul și așa mai departe. De fiecare dată când latura noului pătrat este jumătate din cea precedentă.
Ca rezultat, am obținut o succesiune de laturi ale pătratelor  formând o progresie geometrică cu numitor .
formând o progresie geometrică cu numitor .
Și, ceea ce este foarte important, cu cât construim mai multe astfel de pătrate, cu atât latura pătratului va fi mai mică. de exemplu,

Acestea. pe măsură ce numărul n crește, termenii progresiei se apropie de zero.
Cu ajutorul acestei figuri, mai poate fi luată în considerare o secvență.

De exemplu, succesiunea ariilor pătratelor:

 . Și, din nou, dacă n crește la nesfârșit, apoi zona se apropie de zero în mod arbitrar aproape.
. Și, din nou, dacă n crește la nesfârșit, apoi zona se apropie de zero în mod arbitrar aproape.
Să luăm în considerare încă un exemplu. Un triunghi echilateral cu latura de 1 cm. Să construim următorul triunghi cu vârfuri în punctele mijlocii ale laturilor primului triunghi, conform teoremei liniei mediane a triunghiului - latura celui de-al 2-lea este egală cu jumătatea laturii primului, latura celui de-al 3-lea este jumătatea laturii lui. al 2-lea etc. Din nou obținem o succesiune de lungimi ale laturilor triunghiurilor.
 la
la  .
.
Dacă luăm în considerare o progresie geometrică cu numitor negativ.
Apoi, din nou, cu un număr tot mai mare n termenii progresiei se apropie de zero.
Să fim atenți la numitorii acestor secvențe. Peste tot numitorii au fost mai mici de 1 modulo.
Putem concluziona: o progresie geometrică va fi infinit descrescătoare dacă modulul numitorului ei este mai mic de 1.
Lucru din față.
Definiție:
Se spune că o progresie geometrică este infinit descrescătoare dacă modulul numitorului său este mai mic de unu.  .
.
Cu ajutorul definiției, este posibil să se rezolve întrebarea dacă o progresie geometrică este în scădere infinit sau nu.
Sarcină
Este succesiunea o progresie geometrică infinit descrescătoare dacă este dată de formula:
 ;
;  .
.
Decizie:
 . Sa gasim q
.
. Sa gasim q
.
 ;
;  ;
;  ;
;  .
.
această progresie geometrică este infinit în scădere.
b) această succesiune nu este o progresie geometrică infinit descrescătoare.

Luați în considerare un pătrat cu latura egală cu 1. Împărțiți-l în jumătate, una dintre jumătăți din nou în jumătate și așa mai departe. ariile tuturor dreptunghiurilor rezultate formează o progresie geometrică infinit descrescătoare: ![]()
Suma ariilor tuturor dreptunghiurilor obținute în acest fel va fi egală cu aria primului pătrat și egală cu 1. ![]()
Dar în partea stângă a acestei egalități se află suma unui număr infinit de termeni.
Luați în considerare suma primilor n termeni. ![]()
Conform formulei pentru suma primilor n termeni ai unei progresii geometrice, este egal cu  .
.
În cazul în care un n crește la nesfârșit, atunci
sau  . Asa de
. Asa de  , adică
, adică  .
.
Suma unei progresii geometrice infinit descrescătoare există o limită de secvență S 1 , S 2 , S 3 , …, S n , … .
De exemplu, pentru o progresie  ,
,
 La fel de
La fel de 
Suma unei progresii geometrice infinit descrescătoare poate fi găsit folosind formula 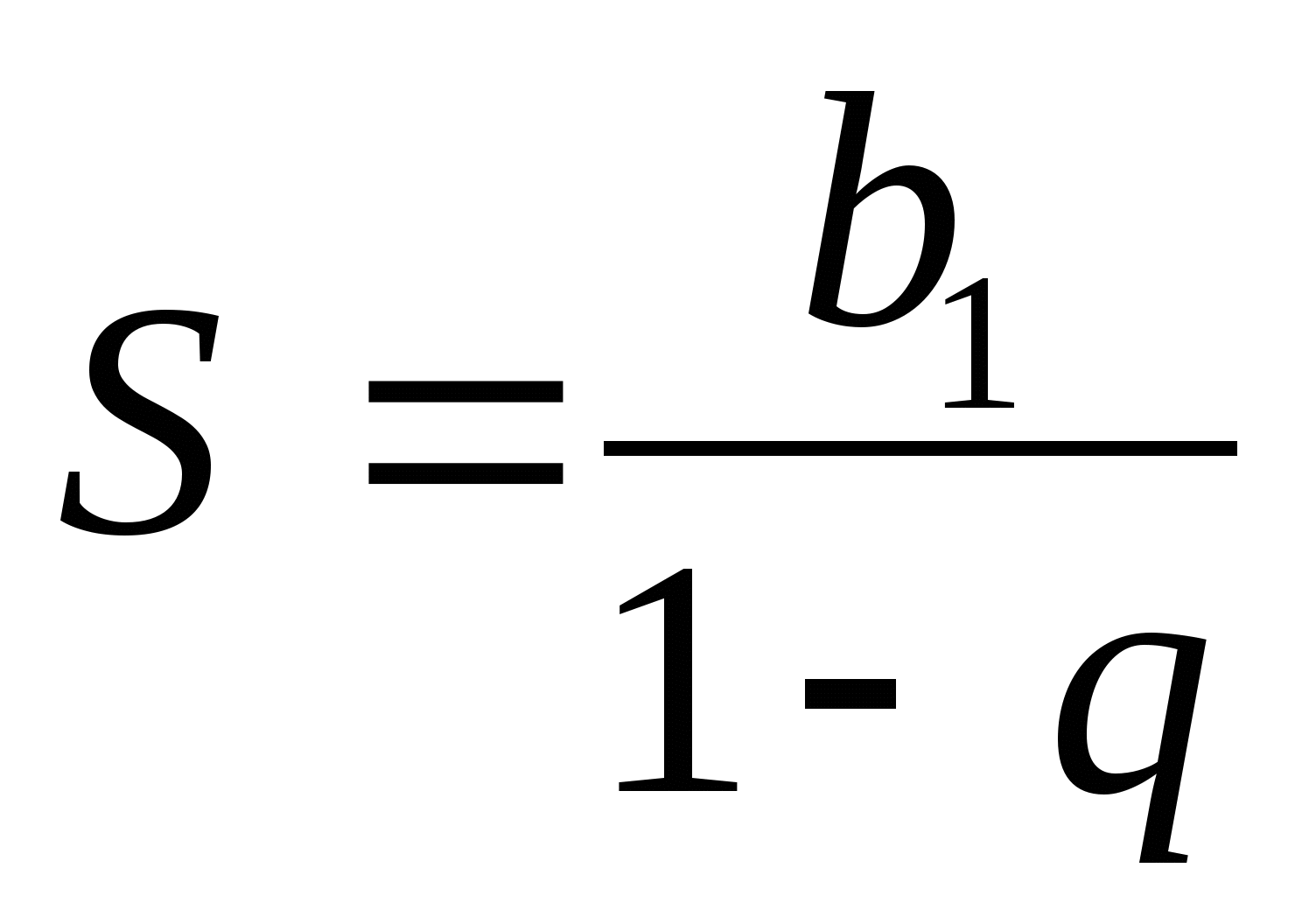 .
.
III . Reflecție și consolidare(finalizarea sarcinilor).
Sarcina numărul 2. Aflați suma unei progresii geometrice infinit descrescătoare cu primul termen 3, al doilea 0,3.
Decizie:
Sarcina numărul 3. manual, p. 160, nr. 433(1)
Aflați suma unei progresii geometrice infinit descrescătoare:
Decizie:

Sarcina numărul 4. Scrieți fracția zecimală periodică infinită 0,(5) ca o fracție comună.
1-a cale. Fie x = 0, (5) = 0,555 ... / 10 Metoda a 2-a. 0,(5)=0,555…=

Sarcina numărul 5. manual, p. 162, nr. 445(3) (decizie independentă)
Scrieți fracția zecimală periodică infinită 0,(12) ca o fracție comună.
Răspuns: 0,(12)=4/33.
IV . Rezumând.
Ce secvență v-ați întâlnit astăzi?
Definiți o progresie geometrică infinit descrescătoare.
Cum se demonstrează că o progresie geometrică este în scădere infinită?
Dați formula pentru suma unei progresii geometrice infinit descrescătoare.
V . Teme pentru acasă.
Lecție și prezentare pe tema: „Secvențe de numere. Progresie geometrică”
Materiale suplimentare
Dragi utilizatori, nu uitați să lăsați comentariile, feedback-ul, sugestiile voastre! Toate materialele sunt verificate de un program antivirus.
Mijloace și simulatoare didactice în magazinul online „Integral” pentru clasa a 9-a
Puteri și rădăcini Funcții și grafice
Băieți, astăzi ne vom familiariza cu un alt tip de progresie.
Tema lecției de astăzi este progresia geometrică.
Progresie geometrică
Definiție. O succesiune numerică în care fiecare termen, începând de la al doilea, este egal cu produsul celui precedent și un număr fix, se numește progresie geometrică.Să definim secvența noastră recursiv: $b_(1)=b$, $b_(n)=b_(n-1)*q$,
unde b și q sunt anumite numere date. Numărul q se numește numitorul progresiei.
Exemplu. 1,2,4,8,16… Progresie geometrică, în care primul membru este egal cu unu și $q=2$.
Exemplu. 8,8,8,8... O progresie geometrică al cărei prim termen este opt,
și $q=1$.
Exemplu. 3,-3,3,-3,3... O progresie geometrică al cărei prim termen este trei,
și $q=-1$.
Progresia geometrică are proprietățile monotonității.
Dacă $b_(1)>0$, $q>1$,
atunci secvența crește.
Dacă $b_(1)>0$, $0 Secvența este de obicei notă ca: $b_(1), b_(2), b_(3), ..., b_(n), ...$.
La fel ca într-o progresie aritmetică, dacă numărul de elemente dintr-o progresie geometrică este finit, atunci progresia se numește progresie geometrică finită.
$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$.
Rețineți că dacă șirul este o progresie geometrică, atunci șirul de termeni pătrați este, de asemenea, o progresie geometrică. A doua secvență are primul termen $b_(1)^2$ și numitorul $q^2$.
Formula celui de-al n-lea membru al unei progresii geometrice
Progresia geometrică poate fi specificată și sub formă analitică. Să vedem cum se face:$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$.
$b_(4)=b_(3)*q=b_(1)*q^3$.
$b_(5)=b_(4)*q=b_(1)*q^4$.
Putem vedea cu ușurință modelul: $b_(n)=b_(1)*q^(n-1)$.
Formula noastră se numește „formula celui de-al n-lea membru al unei progresii geometrice”.
Să revenim la exemplele noastre.
Exemplu. 1,2,4,8,16... O progresie geometrică al cărei prim termen este egal cu unu,
și $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$.
Exemplu. 16,8,4,2,1,1/2… O progresie geometrică al cărei prim termen este șaisprezece și $q=\frac(1)(2)$.
$b_(n)=16*(\frac(1)(2))^(n-1)$.
Exemplu. 8,8,8,8... O progresie geometrică în care primul termen este opt și $q=1$.
$b_(n)=8*1^(n-1)=8$.
Exemplu. 3,-3,3,-3,3... O progresie geometrică al cărei prim termen este trei și $q=-1$.
$b_(n)=3*(-1)^(n-1)$.
Exemplu. Având în vedere o progresie geometrică $b_(1), b_(2), …, b_(n), … $.
a) Se știe că $b_(1)=6, q=3$. Găsiți $b_(5)$.
b) Se știe că $b_(1)=6, q=2, b_(n)=768$. Găsiți n.
c) Se știe că $q=-2, b_(6)=96$. Găsiți $b_(1)$.
d) Se știe că $b_(1)=-2, b_(12)=4096$. Găsiți q.
Decizie.
a) $b_(5)=b_(1)*q^4=6*3^4=486$.
b) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$.
$2^(n-1)=\frac(768)(6)=128$ deoarece $2^7=128 => n-1=7; n=8$.
c) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$.
d) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.
Exemplu. Diferența dintre al șaptelea și al cincilea membru al progresiei geometrice este 192, suma celui de-al cincilea și al șaselea membru al progresiei este 192. Aflați al zecelea membru al acestei progresii.
Decizie.
Știm că: $b_(7)-b_(5)=192$ și $b_(5)+b_(6)=192$.
Mai știm: $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Apoi:
$b_(1)*q^6-b_(1)*q^4=192$.
$b_(1)*q^4+b_(1)*q^5=192$.
Avem un sistem de ecuații:
$\begin(cases)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\end(cases)$.
Echivalând, ecuațiile noastre obțin:
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
Avem două soluții q: $q_(1)=2, q_(2)=-1$.
Înlocuiți succesiv în a doua ecuație:
$b_(1)*2^4*3=192 => b_(1)=4$.
$b_(1)*(-1)^4*0=192 =>$ nicio soluție.
Am obținut că: $b_(1)=4, q=2$.
Să găsim al zecelea termen: $b_(10)=b_(1)*q^9=4*2^9=2048$.
Suma unei progresii geometrice finite
Să presupunem că avem o progresie geometrică finită. Să calculăm, ca și pentru o progresie aritmetică, suma membrilor săi.Să fie dată o progresie geometrică finită: $b_(1),b_(2),…,b_(n-1),b_(n)$.
Să introducem notația pentru suma termenilor săi: $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$.
În cazul în care $q=1$. Toți membrii progresiei geometrice sunt egali cu primul membru, atunci este evident că $S_(n)=n*b_(1)$.
Luați în considerare acum cazul $q≠1$.
Înmulțiți suma de mai sus cu q.
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$.
Notă:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$.
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$.
$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2) )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$.
$S_(n)(q-1)=b_(n)*q-b_(1)$.
$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.
$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$.
Am obținut formula pentru suma unei progresii geometrice finite.
Exemplu.
Aflați suma primilor șapte termeni ai unei progresii geometrice al cărei prim termen este 4 și numitorul este 3.
Decizie.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$.
Exemplu.
Aflați al cincilea membru al progresiei geometrice, care este cunoscut: $b_(1)=-3$; $b_(n)=-3072$; $S_(n)=-4095$.
Decizie.
$b_(n)=(-3)*q^(n-1)=-3072$.
$q^(n-1)=1024$.
$q^(n)=1024q$.
$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$.
$-4095(q-1)=-3*(q^(n)-1)$.
$-4095(q-1)=-3*(1024q-1)$.
$1365q-1365=1024q-1$.
341$ q=1364$.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$.
Proprietatea caracteristică a unei progresii geometrice
Băieți, având în vedere o progresie geometrică. Să luăm în considerare cei trei membri consecutivi ai săi: $b_(n-1),b_(n),b_(n+1)$.Noi stim aia:
$\frac(b_(n))(q)=b_(n-1)$.
$b_(n)*q=b_(n+1)$.
Apoi:
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$.
Dacă progresia este finită, atunci această egalitate este valabilă pentru toți termenii, cu excepția primului și ultimului.
Dacă nu se știe dinainte ce fel de succesiune are șirul, dar se știe că: $b_(n)^(2)=b_(n-1)*b_(n+1)$.
Apoi putem spune cu siguranță că aceasta este o progresie geometrică.
O secvență de numere este o progresie geometrică numai atunci când pătratul fiecăruia dintre termenii săi este egal cu produsul celor doi termeni vecini ai progresiei. Nu uitați că pentru o progresie finită această condiție nu este îndeplinită pentru primul și ultimul termen.
Să ne uităm la această identitate: $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$.
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
$\sqrt(a*b)$ se numește media geometrică a lui a și b.
Modulul oricărui membru al unei progresii geometrice este egal cu media geometrică a celor două elemente adiacente acestuia.
Exemplu.
Găsiți x astfel încât $x+2; 2x+2; 3x+3$ au fost trei membri consecutivi ai unei progresii geometrice.
Decizie.
Să folosim proprietatea caracteristică:
$(2x+2)^2=(x+2)(3x+3)$.
$4x^2+8x+4=3x^2+3x+6x+6$.
$x^2-x-2=0$.
$x_(1)=2$ și $x_(2)=-1$.
Înlocuiți secvențial în expresia originală, soluțiile noastre:
Cu $x=2$, am obținut succesiunea: 4;6;9 este o progresie geometrică cu $q=1.5$.
Cu $x=-1$, avem succesiunea: 1;0;0.
Răspuns: $x=2.$
Sarcini pentru soluție independentă
1. Aflați al optulea prim membru al progresiei geometrice 16; -8; 4; -2 ....2. Aflați al zecelea membru al progresiei geometrice 11,22,44….
3. Se știe că $b_(1)=5, q=3$. Găsiți $b_(7)$.
4. Se știe că $b_(1)=8, q=-2, b_(n)=512$. Găsiți n.
5. Aflați suma primilor 11 membri ai progresiei geometrice 3;12;48….
6. Găsiți x astfel încât $3x+4; 2x+4; x+5$ sunt trei membri consecutivi ai unei progresii geometrice.
SECVENȚE NUMERICE VI
§ l48. Suma unei progresii geometrice infinit descrescătoare
Până acum, vorbind de sume, am presupus întotdeauna că numărul de termeni din aceste sume este finit (de exemplu, 2, 15, 1000 etc.). Dar atunci când rezolvi unele probleme (în special matematica superioară), trebuie să te ocupi de sumele unui număr infinit de termeni
S= A 1 + A 2 + ... + A n + ... . (1)
Care sunt aceste sume? A-prioriu suma unui număr infinit de termeni A 1 , A 2 , ..., A n , ... se numește limita sumei S n primul P numere când P -> ∞ :
S=S n = (A 1 + A 2 + ... + A n ). (2)
Limita (2), desigur, poate exista sau nu. În consecință, se spune că suma (1) există sau nu există.
Cum să aflăm dacă suma (1) există în fiecare caz particular? O soluție generală la această întrebare depășește cu mult scopul programului nostru. Cu toate acestea, există un caz special important pe care trebuie să îl luăm în considerare acum. Vom vorbi despre însumarea termenilor unei progresii geometrice infinit descrescătoare.
Lasa A 1 , A 1 q , A 1 q 2 , ... este o progresie geometrică infinit descrescătoare. Aceasta înseamnă că | q |< 1. Сумма первых P membrii acestei progresii este egal cu
![]()
Din teoremele de bază privind limitele variabilelor (vezi § 136) obținem:

Dar 1 = 1, a q n = 0. Prin urmare

Deci, suma unei progresii geometrice infinit descrescătoare este egală cu primul termen al acestui progres împărțit la unu minus numitorul acestei progresii.
1) Suma progresiei geometrice 1, 1/3, 1/9, 1/27, ... este

iar suma unei progresii geometrice este 12; -6; 3; - 3 / 2 , ... egal

2) O fracție periodică simplă 0,454545 ... se transformă într-una obișnuită.
Pentru a rezolva această problemă, reprezentăm această fracție ca o sumă infinită:
Partea dreaptă a acestei egalități este suma unei progresii geometrice infinit descrescătoare, al cărei prim termen este 45/100, iar numitorul este 1/100. Asa de

În modul descris, se poate obține și regula generală pentru transformarea fracțiilor periodice simple în fracții obișnuite (vezi Capitolul II, § 38):
Pentru a converti o fracție periodică simplă într-una obișnuită, trebuie să procedați după cum urmează: puneți perioada fracției zecimale la numărător, iar la numitor - un număr format din nouă luate de câte ori există cifre în perioadă. a fracției zecimale.
3) Fracția periodică mixtă 0,58333 .... se transformă într-o fracție obișnuită.
Să reprezentăm această fracție ca o sumă infinită:
În partea dreaptă a acestei egalități, toți termenii, începând de la 3/1000, formează o progresie geometrică infinit descrescătoare, al cărei prim termen este 3/1000, iar numitorul este 1/10. Asa de

În modul descris, se poate obține și regula generală pentru conversia fracțiilor periodice mixte în fracții obișnuite (vezi Capitolul II, § 38). Nu îl includem în mod deliberat aici. Nu este nevoie să memorezi această regulă greoaie. Este mult mai util să știm că orice fracție periodică mixtă poate fi reprezentată ca suma unei progresii geometrice infinit descrescătoare și a unui număr. Și formula
pentru suma unei progresii geometrice infinit descrescătoare, trebuie, desigur, să ne amintim.
Ca exercițiu, vă invităm, pe lângă problemele nr. 995-1000 de mai jos, să apelați din nou la problema nr. 301 § 38.
Exerciții
995. Ce se numește suma unei progresii geometrice infinit descrescătoare?
996. Găsiți sume ale progresiilor geometrice infinit descrescătoare:

997. Pentru ce valori X progresie
![]()
scade la infinit? Găsiți suma unei astfel de progresii.
998. Într-un triunghi echilateral cu o latură A un nou triunghi este înscris prin conectarea punctelor medii ale laturilor sale; un nou triunghi este înscris în acest triunghi în același mod și așa mai departe la infinit.
a) suma perimetrelor tuturor acestor triunghiuri;
b) suma suprafețelor acestora.
999. Într-un pătrat cu o latură A un nou pătrat este înscris prin conectarea punctelor medii ale laturilor sale; un pătrat este înscris în acest pătrat în același mod și așa mai departe la infinit. Aflați suma perimetrelor tuturor acestor pătrate și suma ariilor lor.
1000. Faceți o progresie geometrică infinit descrescătoare, astfel încât suma ei să fie egală cu 25 / 4, iar suma pătratelor termenilor săi să fie egală cu 625 / 24.
O progresie geometrică este un nou tip de succesiune de numere cu care trebuie să ne cunoaștem. Pentru o cunoștință de succes, nu strică măcar să cunoască și să înțeleagă. Atunci nu va fi nicio problemă cu progresia geometrică.)
Ce este o progresie geometrică? Conceptul de progresie geometrică.
Începem turul, ca de obicei, cu elementul. Scriu o succesiune neterminată de numere:
1, 10, 100, 1000, 10000, …
Poți să prinzi un model și să spui ce numere vor urma? Ardeiul este limpede, numerele 100000, 1000000 și așa mai departe vor merge mai departe. Chiar și fără prea mult stres mental, totul este clar, nu?)
BINE. Alt exemplu. Scriu următoarea succesiune:
1, 2, 4, 8, 16, …
Puteți spune ce numere vor urma, după numărul 16 și numele Al optulea membru al secvenței? Dacă ți-ai dat seama că ar fi numărul 128, atunci foarte bine. Deci, jumătate din bătălie este în înțelegere sensși puncte cheie progresie geometrică deja făcută. Puteți crește mai departe.)
Și acum trecem din nou de la senzații la matematică riguroasă.
Momente cheie ale unei progresii geometrice.
Momentul cheie #1
Progresia geometrică este succesiune de numere. La fel și progresia. Nimic complicat. Tocmai aranjat această secvență diferit. Prin urmare, desigur, are un alt nume, da...
Momentul cheie #2
Cu al doilea punct cheie, întrebarea va fi mai complicată. Să ne întoarcem puțin și să ne amintim proprietatea cheie a unei progresii aritmetice. Iată-l: fiecare membru este diferit de cel precedent cu aceeași sumă.
Este posibil să se formuleze o proprietate cheie similară pentru o progresie geometrică? Gândiți-vă puțin... Uitați-vă la exemplele date. Ghicit? Da! Într-o progresie geometrică (oricare!) fiecare dintre membrii săi diferă de cel precedent in acelasi numar de ori. Mereu!
În primul exemplu, acest număr este zece. Indiferent de termenul secvenței pe care îl luați, acesta este mai mare decât cel precedent de zece ori.
În al doilea exemplu, acesta este un doi: fiecare membru este mai mare decât precedentul. de două ori.
În acest punct cheie, progresia geometrică diferă de cea aritmetică. Într-o progresie aritmetică, se obține fiecare termen următor adăugând de aceeași valoare cu termenul anterior. Si aici - multiplicare termenul anterior cu aceeași sumă. Asta este diferența.)
Momentul cheie #3
Acest punct cheie este complet identic cu cel pentru o progresie aritmetică. Și anume: fiecare membru al progresiei geometrice este la locul lui. Totul este exact la fel ca în progresia aritmetică, iar comentariile cred că sunt inutile. Există primul termen, există o sută primul și așa mai departe. Să rearanjam cel puțin doi membri - modelul (și odată cu el progresia geometrică) va dispărea. Ceea ce rămâne este doar o succesiune de numere fără nicio logică.
Asta e tot. Acesta este întregul punct al progresiei geometrice.
Termeni și denumiri.
Și acum, după ce ne-am ocupat de semnificația și punctele cheie ale progresiei geometrice, putem trece la teorie. Altfel, ce este o teorie fără a înțelege sensul, nu?
Ce este o progresie geometrică?
Cum se scrie o progresie geometrică în termeni generali? Nici o problema! Fiecare membru al progresiei este scris și sub formă de scrisoare. Numai pentru progresia aritmetică, litera este de obicei folosită "A", pentru geometric - litera „b”. Numarul membrului, ca de obicei, este indicat index dreapta jos. Membrii progresiei înșiși sunt enumerați pur și simplu, separați prin virgule sau punct și virgulă.
Ca aceasta:
b1,b 2 , b 3 , b 4 , b 5 , b 6 , …
Pe scurt, o astfel de progresie este scrisă după cum urmează: (b n) .
Sau astfel, pentru progresii finite:
b 1 , b 2 , b 3 , b 4 , b 5 , b 6 .
b 1 , b 2 , ..., b 29 , b 30 .
Sau, pe scurt:
(b n), n=30 .
Acestea sunt, de fapt, toate desemnările. Totul este la fel, doar litera este diferită, da.) Și acum trecem direct la definiție.
Definirea unei progresii geometrice.
O progresie geometrică este o succesiune numerică, al cărei prim termen este diferit de zero și fiecare termen ulterior este egal cu termenul anterior înmulțit cu același număr diferit de zero.
Asta e toată definiția. Majoritatea cuvintelor și expresiilor vă sunt clare și familiare. Dacă, desigur, nu înțelegeți sensul unei progresii geometrice „pe degete” și în general. Există însă și câteva fraze noi asupra cărora aș dori să atrag o atenție deosebită.
În primul rând, cuvintele: „al cărui prim termen diferit de zero".
Această restricție asupra primului termen nu a fost introdusă întâmplător. Ce crezi că se va întâmpla dacă primul mandat b 1 se dovedește a fi zero? Care va fi al doilea termen dacă fiecare termen este mai mare decât precedentul de acelasi numar de ori? Să spunem de trei ori? Să vedem... Înmulțiți primul termen (adică 0) cu 3 și obțineți... zero! Și al treilea membru? De asemenea, zero! Și al patrulea termen este, de asemenea, zero! etc…
Obținem doar o pungă de covrigi o secvență de zerouri:
0, 0, 0, 0, …
Desigur, o astfel de secvență are dreptul la viață, dar nu are niciun interes practic. Totul este atât de clar. Oricare dintre membrii săi este zero. Suma oricărui număr de membri este, de asemenea, zero... Ce lucruri interesante poți face cu el? Nimic…
Următoarele cuvinte cheie: „înmulțit cu același număr diferit de zero”.
Același număr are și propriul nume special - numitorul unei progresii geometrice. Să începem să ne întâlnim.)
Numitorul unei progresii geometrice.
Totul este simplu.
Numitorul unei progresii geometrice este un număr (sau o valoare) diferit de zero De câte orifiecare membru al progresiei mai mult decât precedentul.
Din nou, prin analogie cu progresia aritmetică, cuvântul cheie la care trebuie să acordați atenție în această definiție este cuvântul "Mai mult". Înseamnă că se obține fiecare termen al unei progresii geometrice multiplicare chiar la acest numitor membru anterior.
Explic.
Pentru a calcula, să zicem al doilea membru să ia primul membru și multiplica ea la numitor. Pentru calcul al zecelea membru să ia nouălea membru și multiplica ea la numitor.
Numitorul progresiei geometrice în sine poate fi orice. Absolut oricine! Număr întreg, fracțional, pozitiv, negativ, irațional - toată lumea. În afară de zero. Despre asta ne spune cuvântul „non-zero” din definiție. De ce este nevoie de acest cuvânt aici - mai multe despre asta mai târziu.
Numitorul unei progresii geometrice notată de obicei printr-o literă q.
Cum să-l găsesc pe acesta q? Nici o problema! Trebuie să luăm orice termen al progresiei și împărțiți la termenul anterior. Diviziunea este fracțiune. De aici și numele - „numitorul progresiei”. Numitorul, de obicei se află într-o fracție, da ...) Deși, logic, valoarea q ar trebui chemat privat progresie geometrică, asemănătoare cu diferență pentru o progresie aritmetică. Dar a fost de acord să sun numitor. Și nici nu vom reinventa roata.)
Să definim, de exemplu, valoarea q pentru această progresie geometrică:
2, 6, 18, 54, …
Totul este elementar. Luăm orice număr de secvență. Ceea ce vrem este ceea ce luăm. În afară de primul. De exemplu, 18. Și împărțiți la numărul anterior. Adică la 6.
Primim:
q = 18/6 = 3
Asta e tot. Acesta este răspunsul corect. Pentru o anumită progresie geometrică, numitorul este trei.
Să găsim numitorul q pentru o altă progresie geometrică. De exemplu, așa:
1, -2, 4, -8, 16, …
Tot la fel. Indiferent de semnele pe care membrii înșiși le au, noi încă luăm orice numărul de ordine (de exemplu, 16) și împărțiți cu numărul anterior(adică -8).
Primim:
d = 16/(-8) = -2
Și asta este.) De data aceasta, numitorul progresiei s-a dovedit a fi negativ. Minus doi. S-a întâmplat.)
Să luăm această progresie:
1, 1/3, 1/9, 1/27, …
Și din nou, indiferent de tipul de numere din șir (chiar și numere întregi, chiar fracționale, chiar negative, chiar iraționale), luăm orice număr (de exemplu, 1/9) și împărțim la numărul anterior (1/3). Conform regulilor operațiunilor cu fracții, desigur.
Primim:
Asta e tot.) Aici numitorul s-a dovedit a fi fracționar: q = 1/3.
Dar o astfel de „progresie” ca tine?
3, 3, 3, 3, 3, …
Evident aici q = 1 . Formal, aceasta este și o progresie geometrică, doar cu aceiași membri.) Dar astfel de progresii nu sunt interesante pentru studiu și aplicare practică. La fel ca progresiile cu zerouri solide. Prin urmare, nu le vom lua în considerare.
După cum puteți vedea, numitorul progresiei poate fi orice - întreg, fracționar, pozitiv, negativ - orice! Nu poate fi doar zero. Nu ai ghicit de ce?
Ei bine, să ne uităm la un exemplu specific, ce se va întâmpla dacă luăm ca numitor q zero.) Să avem, de exemplu b 1 = 2 , A q = 0 . Care va fi atunci al doilea mandat?
Noi credem:
b 2 = b 1 · q= 2 0 = 0
Și al treilea membru?
b 3 = b 2 · q= 0 0 = 0
Tipuri și comportament ale progresiilor geometrice.
Cu totul era mai mult sau mai puțin clar: dacă diferența în progresie d este pozitiv, progresia este în creștere. Dacă diferența este negativă, atunci progresia scade. Există doar două opțiuni. Nu există a treia.)
Dar cu comportamentul unei progresii geometrice, totul va fi mult mai interesant și mai divers!)
De îndată ce membrii se comportă aici: cresc și scad, și se apropie la infinit de zero, și chiar schimbă semnele, grăbindu-se alternativ fie la „plus”, fie la „minus”! Și în toată această diversitate trebuie să poți înțelege bine, da...
Înțelegem?) Să începem cu cel mai simplu caz.
Numitorul este pozitiv ( q >0)
Cu un numitor pozitiv, în primul rând, membrii unei progresii geometrice pot intra în plus infinit(adică crește pe termen nelimitat) și poate intra în minus infinitul(adică scăderea pe termen nelimitat). Ne-am obișnuit deja cu un astfel de comportament al progresiilor.
De exemplu:
(b n): 1, 2, 4, 8, 16, …
Totul este simplu aici. Fiecare membru al progresiei este mai mult decât precedentul. Și fiecare membru primește multiplicare membru anterior pe pozitiv numărul +2 (adică q = 2 ). Comportamentul unei astfel de progresii este evident: toți membrii progresiei cresc la infinit, mergând în spațiu. Plus infinitul...
Acum iată progresia:
(b n): -1, -2, -4, -8, -16, …
Și aici se obține fiecare termen al progresiei multiplicare membru anterior pe pozitiv numărul +2. Dar comportamentul unei astfel de progresii este deja direct opus: fiecare membru al progresiei este obținut mai puțin decât anterior, iar toți termenii săi scad la infinit, ajungând la minus infinit.
Acum să ne gândim: ce au aceste două progresii în comun? Așa este, numitor! Aici si acolo q = +2 . Număr pozitiv. Egalitate de puncte. Si aici comportament Aceste două progresii sunt fundamental diferite! Nu ai ghicit de ce? Da! Este vorba despre primul membru! El este, după cum se spune, cel care comandă muzica.) Vedeți singur.
În primul caz, primul termen al progresiei pozitiv(+1) și, prin urmare, toți termenii următori obținuți prin înmulțirea cu pozitiv numitor q = +2 , va de asemenea pozitiv.
Dar în al doilea caz, primul termen negativ(-unu). Prin urmare, toți membrii ulterioare ai progresiei obținute prin înmulțirea cu pozitiv q = +2 , se va obtine de asemenea negativ. Pentru „minus” la „plus” dă întotdeauna „minus”, da.)
După cum puteți vedea, spre deosebire de o progresie aritmetică, o progresie geometrică se poate comporta în moduri complet diferite, nu numai în funcție de de la numitorq, dar și în funcție de la primul membru, Da.)
Amintiți-vă: comportamentul unei progresii geometrice este determinat în mod unic de primul ei membru b 1 și numitorulq .
Și acum începem analiza unor cazuri mai puțin familiare, dar mult mai interesante!
Luați, de exemplu, următoarea secvență:
(b n): 1, 1/2, 1/4, 1/8, 1/16, …
Această secvență este și o progresie geometrică! Se obține și fiecare membru al acestei progresii multiplicare termenul anterior, cu același număr. Doar numărul este fractionar: q = +1/2 . Sau +0,5 . Și numărul (important!), unul mai mic:q = 1/2<1.
Ce este interesant la această progresie geometrică? Unde merg membrii săi? Să aruncăm o privire:
1/2 = 0,5;
1/4 = 0,25;
1/8 = 0,125;
1/16 = 0,0625;
…….
Ce este interesant aici? În primul rând, scăderea membrilor progresiei este imediat izbitoare: fiecare dintre membrii săi mai mici precedentul exact de 2 ori. Sau, conform definiției unei progresii geometrice, fiecare termen Mai mult anterior de 1/2 ori, deoarece numitorul de progresie q = 1/2 . Și de la înmulțirea cu un număr pozitiv mai mic de unu, rezultatul scade de obicei, da ...
Ce Mai mult se poate observa în comportamentul acestei progresii? Membrii săi dispar? nelimitat, merge la minus infinit? Nu! Ele dispar într-un mod special. La început scad destul de repede, apoi din ce în ce mai încet. Și tot timpul stând pozitiv. Deși foarte, foarte mic. Și pentru ce se străduiesc? Nu ai ghicit? Da! Ei tind la zero!) Și, atenție, membrii progresiei noastre nu ajunge niciodată! Numai infinit aproape de el. Este foarte important.)
O situație similară va fi într-o astfel de progresie:
(b n): -1, -1/2, -1/4, -1/8, -1/16, …
Aici b 1 = -1 , A q = 1/2 . Totul este la fel, doar că acum membrii se vor apropia de zero din cealaltă parte, de jos. Stau tot timpul negativ.)
O astfel de progresie geometrică, ai cărei membri apropiindu-se de zero la infinit.(nu contează, pe partea pozitivă sau negativă), în matematică are un nume special - progresie geometrică infinit descrescătoare. Această progresie este atât de interesantă și neobișnuită încât chiar va fi lecție separată .)
Deci, am considerat tot posibilul pozitiv numitorii sunt atât mari, cât și mai mici. Nu îl considerăm pe cel în sine drept numitor din motivele expuse mai sus (amintiți-vă exemplul cu succesiunea triplelor...)
A rezuma:
pozitivși mai mult de o (q>1), apoi membrii progresiei:
A) crește la nesfârșit (dacăb 1 >0);
b) scade pe termen nelimitat (dacab 1 <0).
Dacă numitorul unei progresii geometrice pozitiv și mai putin de unul (0< q<1), то члены прогрессии:
a) infinit aproape de zero de mai sus(dacăb 1 >0);
b) infinit aproape de zero de desubt(dacăb 1 <0).
Rămâne acum să luăm în considerare cazul numitor negativ.
Numitorul este negativ ( q <0)
Nu vom merge departe pentru un exemplu. De ce, de fapt, bunica shaggy?!) Să fie, de exemplu, primul membru al progresiei b 1 = 1 , și luați numitorul q = -2.
Obținem următoarea secvență:
(b n): 1, -2, 4, -8, 16, …
Și așa mai departe.) Se obține fiecare termen al progresiei multiplicare membru anterior pe un număr negativ-2. În acest caz, toți membrii aflați pe locuri impare (primul, al treilea, al cincilea etc.) vor fi pozitiv, și în locuri pare (al doilea, al patrulea etc.) - negativ. Semnele sunt strict intercalate. Plus-minus-plus-minus ... O astfel de progresie geometrică se numește - semn crescător alternând.
Unde merg membrii săi? Și nicăieri.) Da, în valoare absolută (adică modulo) termenii progresiei noastre cresc la nesfârşit (de unde şi denumirea de „în creştere”). Dar, în același timp, fiecare membru al progresiei îl aruncă alternativ în căldură, apoi în frig. Fie plus, fie minus. Progresia noastră fluctuează... Mai mult, gama de fluctuații crește rapid cu fiecare pas, da.) Prin urmare, aspirațiile membrilor progresiei de a merge undeva specific Aici Nu. Nici la plus infinit, nici la minus infinit, nici la zero - nicăieri.
Luați în considerare acum un numitor fracțional între zero și minus unu.
De exemplu, lasă-l să fie b 1 = 1 , A q = -1/2.
Apoi obținem progresia:
(b n): 1, -1/2, 1/4, -1/8, 1/16, …
Și din nou avem o alternanță de semne! Dar, spre deosebire de exemplul precedent, aici există deja o tendință clară ca termenii să se apropie de zero.) Numai că de data aceasta termenii noștri se apropie de zero nu strict de sus sau de jos, ci din nou. ezitând. Luând alternativ valori pozitive sau negative. Dar în același timp ei module sunt din ce în ce mai aproape de prețul zero.)
Această progresie geometrică se numește semn alternant descrescator infinit.
De ce sunt interesante aceste două exemple? Și faptul că în ambele cazuri are loc caractere alternante! Un astfel de cip este tipic doar pentru progresiile cu numitor negativ, da.) Prin urmare, dacă într-o anumită sarcină vedeți o progresie geometrică cu membri alternanți, atunci veți ști deja că numitorul său este 100% negativ și nu vă veți înșela. în semn.)
Apropo, în cazul unui numitor negativ, semnul primului termen nu afectează deloc comportamentul progresiei în sine. Oricare ar fi semnul primului membru al progresiei, în orice caz, se va respecta semnul alternanței membrilor. Întreaga întrebare este justă in ce locuri(par sau impar) vor fi membri cu semne specifice.
Tine minte:
Dacă numitorul unei progresii geometrice negativ , atunci semnele termenilor progresiei sunt întotdeauna alterna.
În același timp, membrii înșiși:
a) crește pe termen nelimitatmodulo, dacăq<-1;
b) se apropie de zero la infinit dacă -1< q<0 (прогрессия бесконечно убывающая).
Asta e tot. Toate cazurile tipice sunt analizate.)
În procesul de analiză a unei varietăți de exemple de progresii geometrice, am folosit periodic cuvintele: "tinde spre zero", „tinde spre plus infinit”, tinde spre minus infinit... Este în regulă.) Aceste rânduri de vorbire (și exemplele specifice) sunt doar o cunoaștere inițială cu comportament diverse secvențe de numere. Un exemplu de progresie geometrică.
De ce trebuie să cunoaștem comportamentul de progresie? Ce diferență are unde merge ea? La zero, la plus infinit, la minus infinit... Ce ne pasă de asta?
Chestia este că deja la universitate, în cursul matematicii superioare, veți avea nevoie de capacitatea de a lucra cu o varietate de secvențe numerice (cu orice, nu doar progresii!) Și capacitatea de a vă imagina exact cum se comportă cutare sau cutare secvență. - dacă crește este nelimitat, dacă scade, dacă tinde către un anumit număr (și nu neapărat către zero), sau chiar nu tinde spre nimic... O întreagă secțiune este dedicată acestui subiect în cursul analiza matematica - teoria limitei. Puțin mai concret, conceptul limita succesiunii de numere. Foarte interesant subiectul! Are sens să mergi la facultate și să-ți dai seama.)
Câteva exemple din această secțiune (secvențe care au o limită) și în special, progresie geometrică infinit descrescătoareîncepe să învețe la școală. Se obișnuiește.)
Mai mult decât atât, capacitatea de a studia bine comportamentul secvențelor în viitor va juca foarte mult în mâini și va fi foarte utilă în cercetarea funcţiei. Cele mai variate. Dar capacitatea de a lucra cu competență cu funcții (a calcula derivate, a le explora în întregime, a le construi grafice) vă crește deja dramatic nivelul matematic! Îndoială? Nu este nevoie. Amintește-ți și cuvintele mele.)
Să ne uităm la o progresie geometrică în viață?
În viața din jurul nostru, întâlnim o progresie exponențială foarte, foarte des. Fără să știe.)
De exemplu, diverse microorganisme care ne înconjoară peste tot în cantități uriașe și pe care nici măcar nu le vedem fără microscop se înmulțesc tocmai în progresie geometrică.
Să presupunem că o bacterie se reproduce prin împărțirea în jumătate, dând urmași în 2 bacterii. La rândul lor, fiecare dintre ei, înmulțindu-se, se împarte și la jumătate, dând un descendent comun de 4 bacterii. Următoarea generație va da 8 bacterii, apoi 16 bacterii, 32, 64 și așa mai departe. Cu fiecare generație succesivă, numărul bacteriilor se dublează. Un exemplu tipic de progresie geometrică.)
De asemenea, unele insecte - afidele, muștele - se înmulțesc exponențial. Și uneori și iepurii, apropo.)
Un alt exemplu de progresie geometrică, mai apropiată de viața de zi cu zi, este așa-numita interes compus. Un astfel de fenomen interesant se găsește adesea în depozitele bancare și se numește capitalizarea dobânzii. Ce este?
Tu însuți ești încă, desigur, tânăr. Înveți la școală, nu aplici la bănci. Dar părinții tăi sunt adulți și oameni independenți. Ei merg la muncă, câștigă bani pentru pâinea lor zilnică și pun o parte din bani în bancă, făcând economii.)
Să presupunem că tatăl tău vrea să economisească o anumită sumă de bani pentru o vacanță de familie în Turcia și să pună 50.000 de ruble în bancă la 10% pe an pentru o perioadă de trei ani cu capitalizare anuală a dobânzii. Mai mult, nimic nu se poate face cu depozitul în toată această perioadă. Nu puteți nici să reîncărcați depozitul și nici să retrageți bani din cont. Ce profit va face în acești trei ani?
Ei bine, în primul rând, trebuie să vă dați seama ce este 10% pe an. Înseamnă că intr-un an 10% va fi adăugat la suma inițială a depozitului de către bancă. De la ce? Desigur, de la suma inițială a depozitului.
Calculați suma contului într-un an. Dacă suma inițială a depozitului a fost de 50.000 de ruble (adică 100%), atunci într-un an câtă dobândă va fi pe cont? Așa e, 110%! De la 50.000 de ruble.
Deci luăm în considerare 110% din 50.000 de ruble:
50.000 1,1 \u003d 55.000 de ruble.
Sper că înțelegeți că găsirea a 110% din valoare înseamnă înmulțirea acestei valori cu numărul 1,1? Dacă nu înțelegeți de ce este așa, amintiți-vă de clasele a cincea și a șasea. Și anume - relația procentelor cu fracțiile și părțile.)
Astfel, creșterea pentru primul an va fi de 5000 de ruble.
Câți bani vor fi în cont după doi ani? 60.000 de ruble? Din păcate (sau mai bine zis, din fericire), nu este atât de simplu. Întregul truc al capitalizării dobânzii este că, cu fiecare nouă dobândă acumulată, aceleași dobânzi vor fi deja luate în considerare din noua sumă! De la cel care deja este pe cont Pentru moment. Iar dobânda acumulată pentru termenul anterior se adaugă la suma inițială a depozitului și, astfel, ei înșiși participă la calculul dobânzii noi! Adică devin o parte integrală a contului total. sau generală capital. De aici și numele - capitalizarea dobânzii.
Este în economie. Și în matematică se numesc astfel de procente interes compus. Sau procente din procente.) Trucul lor este că în calculul secvenţial, procentele sunt calculate de fiecare dată din noua valoare. Nu din original...
Prin urmare, pentru a calcula suma prin doi ani, trebuie să calculăm 110% din suma care va fi în cont intr-un an. Adică, deja de la 55.000 de ruble.
Considerăm 110% din 55.000 de ruble:
55000 1,1 \u003d 60500 ruble.
Aceasta înseamnă că creșterea procentuală pentru al doilea an va fi deja de 5.500 de ruble, iar timp de doi ani - 10.500 de ruble.
Acum puteți deja ghici că în trei ani suma din cont va fi de 110% din 60.500 de ruble. Adică din nou 110% din precedentul (anul trecut) sume.
Aici luăm în considerare:
60500 1,1 \u003d 66550 ruble.
Și acum ne construim sumele monetare pe ani în succesiune:
50000;
55000 = 50000 1,1;
60500 = 55000 1,1 = (50000 1,1) 1,1;
66550 = 60500 1,1 = ((50000 1,1) 1,1) 1,1
Așa cum? De ce nu o progresie geometrică? Primul membru b 1 = 50000 , și numitorul q = 1,1 . Fiecare termen este strict de 1,1 ori mai mare decât cel anterior. Totul este în strictă conformitate cu definiția.)
Și câte bonusuri procentuale suplimentare va „va introduce” tatăl tău în timp ce cele 50.000 de ruble ale sale au fost în contul bancar timp de trei ani?
Noi credem:
66550 - 50000 = 16550 ruble
E rău, desigur. Dar asta dacă suma inițială a contribuției este mică. Dacă sunt mai multe? Să spunem, nu 50, ci 200 de mii de ruble? Apoi, creșterea timp de trei ani va fi deja de 66.200 de ruble (dacă socotiți). Ceea ce este deja foarte bun.) Și dacă contribuția este și mai mare? Asta e...
Concluzie: cu cât contribuția inițială este mai mare, cu atât capitalizarea dobânzii devine mai profitabilă. De aceea depozitele cu capitalizare de dobanda sunt asigurate de banci pe perioade lungi. Să zicem cinci ani.
De asemenea, tot felul de boli rele precum gripa, rujeola și boli chiar mai teribile (același SARS la începutul anilor 2000 sau ciuma în Evul Mediu) le place să se răspândească exponențial. De aici amploarea epidemilor, da...) Și totul din cauza faptului că o progresie geometrică cu întreg numitor pozitiv (q>1) - un lucru care crește foarte repede! Amintiți-vă de reproducerea bacteriilor: dintr-o bacterie se obțin două, din două - patru, din patru - opt și așa mai departe ... Odată cu răspândirea oricărei infecții, totul este la fel.)
Cele mai simple probleme de progresie geometrică.
Să începem, ca întotdeauna, cu o simplă problemă. Pur și simplu pentru a înțelege sensul.
1. Se știe că al doilea termen al unei progresii geometrice este 6, iar numitorul este -0,5. Găsiți primul, al treilea și al patrulea termen.
Deci ni se dau fără sfârşit progresie geometrică, binecunoscută al doilea membru această progresie:
b2 = 6
În plus, știm și noi numitorul de progresie:
q = -0,5
Și trebuie să găsești primul, al treileași Al patrulea membri ai acestei progresii.
Aici acționăm. Scriem succesiunea în funcție de starea problemei. Direct în termeni generali, unde al doilea membru este cei șase:
b1,6,b 3 , b 4 , …
Acum să începem să căutăm. Începem, ca întotdeauna, cu cele mai simple. Puteți calcula, de exemplu, al treilea termen b 3? Poate sa! Știm deja (direct în sensul unei progresii geometrice) că al treilea termen (b 3) mai mult de o secundă (b 2 ) în "q" o singura data!
Deci scriem:
b 3 =b 2 · q
Înlocuim cele șase în această expresie în loc de b 2și -0,5 în schimb qși gândim. Și nici minusul nu este ignorat, desigur...
b 3 \u003d 6 (-0,5) \u003d -3
Ca aceasta. Al treilea termen s-a dovedit a fi negativ. Nu e de mirare: numitorul nostru q- negativ. Și plusul înmulțit cu minus, va fi, desigur, minus.)
Acum luăm în considerare următorul, al patrulea termen al progresiei:
b 4 =b 3 · q
b 4 \u003d -3 (-0,5) \u003d 1,5
Al patrulea termen este din nou cu un plus. Al cincilea termen va fi din nou cu un minus, al șaselea cu un plus și așa mai departe. Semne - alternativ!
Deci, al treilea și al patrulea membru au fost găsiți. Rezultatul este următoarea succesiune:
b1; 6; -3; 1,5; …
Rămâne acum să găsim primul termen b 1 după binecunoscuta secundă. Pentru a face acest lucru, pășim în cealaltă direcție, spre stânga. Aceasta înseamnă că, în acest caz, nu trebuie să înmulțim al doilea termen al progresiei cu numitorul, ci acțiune.
Împărțim și obținem:
![]()
Asta e tot.) Răspunsul la problemă va fi următorul:
-12; 6; -3; 1,5; …
După cum puteți vedea, principiul soluției este același ca în . Noi stim orice membru și numitor progresie geometrică – putem găsi orice alt termen. Orice ne dorim, vom găsi unul.) Singura diferență este că adunarea/scăderea este înlocuită cu înmulțirea/împărțirea.
Amintiți-vă: dacă cunoaștem cel puțin un membru și un numitor al unei progresii geometrice, atunci putem găsi întotdeauna orice alt membru al acestei progresii.
Următoarea sarcină, conform tradiției, este din versiunea reală a OGE:
2.
…; 150; X; 6; 1,2; …
Așa cum? De data aceasta nu există un prim termen, nici un numitor q, se dă doar o secvență de numere... Ceva familiar deja, nu? Da! O problemă similară a fost deja tratată în progresia aritmetică!
Aici nu ne este frică. Tot la fel. Întoarce-ți capul și amintește-ți semnificația elementară a unei progresii geometrice. Ne uităm cu atenție la secvența noastră și ne dăm seama ce parametri ai progresiei geometrice a celor trei principale (primul membru, numitorul, numărul membrului) sunt ascunși în ea.
Numerele membrilor? Nu există numere de membri, da... Dar sunt patru succesiv numerele. Ce înseamnă acest cuvânt, nu văd rostul să explic în acest stadiu.) Are there two numere cunoscute vecine? Există! Acestea sunt 6 și 1.2. Deci putem găsi numitorul de progresie. Deci luăm numărul 1,2 și împărțim la numărul anterior. Pentru șase.
Primim:
Primim:
X= 150 0,2 = 30
Răspuns: X = 30 .
După cum puteți vedea, totul este destul de simplu. Principala dificultate constă doar în calcule. Este deosebit de dificil în cazul numitorilor negativi și fracționali. Deci cei care au probleme, repeta aritmetica! Cum să lucrezi cu fracții, cum să lucrezi cu numere negative și așa mai departe... În caz contrar, vei încetini fără milă aici.
Acum să schimbăm puțin problema. Acum va deveni interesant! Să eliminăm ultimul număr 1.2 din el. Să rezolvăm această problemă acum:
3. Se scriu mai mulți termeni consecutivi ai unei progresii geometrice:
…; 150; X; 6; …
Găsiți termenul progresiei, notat cu litera x.
Totul este la fel, doar două vecine celebru nu mai avem membri ai progresiei. Aceasta este problema principală. Pentru că amploarea q prin doi termeni vecini, putem deja determina cu ușurință nu putem. Avem șansa de a face față provocării? Cu siguranță!
Să scriem termenul necunoscut „ X„Direct în sensul unei progresii geometrice! În termeni generali.
Da Da! Direct cu numitor necunoscut!
Pe de o parte, pentru x putem scrie următorul raport:
X= 150q
Pe de altă parte, avem tot dreptul să pictăm același X Următorul membru, prin cei sase! Împărțiți șase la numitor.
Ca aceasta:
X = 6/ q
Evident, acum putem echivala ambele aceste rapoarte. Din moment ce ne exprimăm aceeași valoarea (x), dar două căi diferite.
Obtinem ecuatia:
Înmulțind totul cu q, simplificând, reducând, obținem ecuația:
q 2 \u003d 1/25
Rezolvăm și obținem:
q = ±1/5 = ±0,2
Hopa! Numitorul este dublu! +0,2 și -0,2. Și pe care să o aleg? Capat de drum?
Calm! Da, problema chiar are doua solutii! Nimic în neregulă cu asta. Se întâmplă.) Nu ești surprins când, de exemplu, obții două rădăcini rezolvând obișnuitul? Este aceeași poveste aici.)
Pentru q = +0,2 vom lua:
X \u003d 150 0,2 \u003d 30
Si pentru q = -0,2 voi:
X = 150 (-0,2) = -30
Primim un răspuns dublu: X = 30; X = -30.
Ce înseamnă acest fapt interesant? Și ce există două progresii, satisfacand starea problemei!
Ca acestea:
…; 150; 30; 6; …
…; 150; -30; 6; …
Ambele sunt potrivite.) Care crezi că este motivul bifurcării răspunsurilor? Doar din cauza eliminării unui membru specific al progresiei (1,2), care vine după șase. Și cunoscând doar membrii anterioare (n-1) și ulterioare (n+1) ale progresiei geometrice, nu mai putem spune fără echivoc nimic despre al n-lea membru care se află între ei. Există două opțiuni - plus și minus.
Dar nu contează. De regulă, în sarcinile pentru o progresie geometrică există informații suplimentare care oferă un răspuns fără ambiguitate. Să spunem cuvintele: „progresie alternantă cu semne” sau "progresie cu numitor pozitiv"și așa mai departe... Aceste cuvinte ar trebui să servească drept indiciu care semn, plus sau minus, ar trebui să fie ales atunci când se face răspunsul final. Dacă nu există astfel de informații, atunci - da, sarcina va avea doua solutii.)
Și acum decidem singuri.
4. Stabiliți dacă numărul 20 va fi membru al unei progresii geometrice:
4 ; 6; 9; …
5. Se dă o progresie geometrică alternativă:
…; 5; X ; 45; …
Găsiți termenul progresiei indicat de literă X .
6. Găsiți al patrulea termen pozitiv al progresiei geometrice:
625; -250; 100; …
7. Al doilea termen al progresiei geometrice este -360, iar al cincilea termen este 23,04. Găsiți primul termen al acestei progresii.
Răspunsuri (în dezordine): -15; 900; Nu; 2,56.
Felicitari daca totul a iesit!
Ceva nu se potrivește? Există undeva un răspuns dublu? Citim cu atentie conditiile misiunii!
Ultimul puzzle nu merge? Nimic complicat acolo.) Lucrăm direct după semnificația unei progresii geometrice. Ei bine, poți desena o imagine. Ajută.)
După cum puteți vedea, totul este elementar. Dacă progresia este scurtă. Dacă e lung? Sau numărul membrului dorit este foarte mare? Aș dori, prin analogie cu o progresie aritmetică, să obțin cumva o formulă convenabilă care să o facă ușor de găsit orice membru al oricărei progresii geometrice după numărul lui. Fără a înmulți de multe, de multe ori cu q. Și există o astfel de formulă!) Detalii - în lecția următoare.


