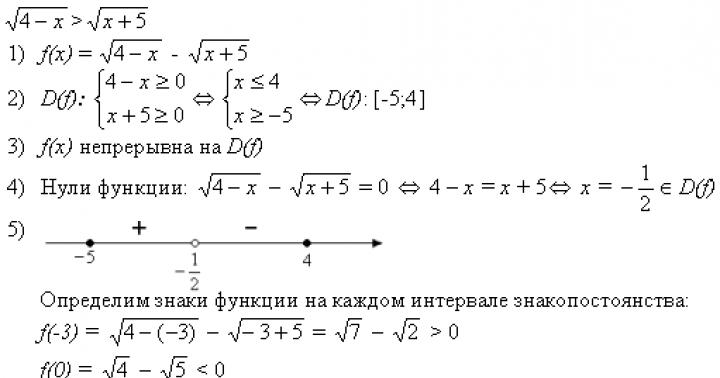Μέθοδοι επίλυσης παράλογων ανισοτήτων με αναλυτική λύση. Παράλογες ανισότητες. Προστασία προσωπικών πληροφοριών

Στόχοι:

1. Γενική εκπαίδευση: συστηματοποίηση, γενίκευση, διεύρυνση των γνώσεων και των δεξιοτήτων των μαθητών που σχετίζονται με την εφαρμογή μεθόδων επίλυσης ανισοτήτων.
2. Αναπτυξιακή: ανάπτυξη στους μαθητές της ικανότητας να ακούν μια διάλεξη, γράφοντάς τη συνοπτικά σε ένα σημειωματάριο.
3. Εκπαιδευτικό: για τη δημιουργία γνωστικών κινήτρων για τη μελέτη των μαθηματικών.

Κατά τη διάρκεια των μαθημάτων

I. Εισαγωγική συνομιλία:

Τελειώσαμε το θέμα «Επίλυση παράλογων εξισώσεων» και σήμερα αρχίζουμε να μαθαίνουμε πώς να λύνουμε παράλογες ανισότητες.

Αρχικά, ας θυμηθούμε ποιους τύπους ανισοτήτων μπορείτε να λύσετε και με ποιες μεθόδους;

Απάντηση: Γραμμικό, τετράγωνο, ορθολογικό, τριγωνομετρικό. Οι γραμμικές λύνονται με βάση τις ιδιότητες των ανισώσεων, οι τριγωνομετρικές ανάγονται στις απλούστερες τριγωνομετρικές, επιλύονται με τριγωνομετρικό κύκλο και οι υπόλοιπες, κυρίως με τη μέθοδο των διαστημάτων.

Ερώτηση: Σε ποια δήλωση βασίζεται η μέθοδος των διαστημάτων;

Απάντηση: Σε ένα θεώρημα που δηλώνει ότι μια συνεχής συνάρτηση που δεν εξαφανίζεται σε κάποιο διάστημα διατηρεί το πρόσημό της σε αυτό το διάστημα.

II.Ας θεωρήσουμε μια παράλογη ανισότητα όπως >

Ερώτηση: Είναι δυνατόν να εφαρμοστεί η μέθοδος διαστήματος για την επίλυσή του;

Απάντηση: Ναι, από τη λειτουργία y=- συνεχής ενεργοποίηση D(y).

Λύνουμε αυτήν την ανισότητα μέθοδος διαστήματος .

Συμπέρασμα: λύσαμε πολύ εύκολα αυτήν την παράλογη ανισότητα με τη μέθοδο του διαστήματος, μειώνοντάς την στην επίλυση μιας παράλογης εξίσωσης.

Ας προσπαθήσουμε να λύσουμε μια άλλη ανισότητα με αυτή τη μέθοδο.

3)f(x)συνεχής ενεργή Δ(στ)

4) Μηδενικά συναρτήσεων:

• Μακρά αναζήτηση Δ(στ).
• Είναι δύσκολο να υπολογιστούν τα σημεία διακοπής.

Τίθεται το ερώτημα: «Υπάρχουν άλλοι τρόποι να λυθεί αυτή η ανισότητα;».

Προφανώς, υπάρχει και τώρα θα τους γνωρίσουμε.

III.Ετσι, θέμα σημερινή μάθημα: «Μέθοδοι επίλυσης παράλογων ανισοτήτων».

Το μάθημα θα διεξαχθεί σε μορφή διάλεξης, αφού το σχολικό βιβλίο δεν περιέχει λεπτομερή ανάλυση όλων των μεθόδων. Επομένως, το σημαντικό μας καθήκον είναι να συντάξουμε μια λεπτομερή περίληψη αυτής της διάλεξης.

IV.Έχουμε ήδη μιλήσει για την πρώτη μέθοδο επίλυσης παράλογων ανισοτήτων.

Αυτό - μέθοδος διαστήματος , μια καθολική μέθοδος για την επίλυση όλων των τύπων ανισοτήτων. Αλλά δεν οδηγεί πάντα στον στόχο με σύντομο και απλό τρόπο.

v.Όταν λύνετε παράλογες ανισώσεις, μπορείτε να χρησιμοποιήσετε τις ίδιες ιδέες όπως όταν λύνετε παράλογες εξισώσεις, αλλά επειδή η απλή επαλήθευση των λύσεων είναι αδύνατη (εξάλλου, οι λύσεις των ανισώσεων είναι συνήθως ακέραια αριθμητικά διαστήματα), είναι απαραίτητο να χρησιμοποιήσετε ισοδυναμία.

Παρουσιάζουμε σχήματα για την επίλυση των κύριων τύπων παράλογων ανισοτήτων μέθοδος ισοδύναμων μεταβάσεωναπό μια ανισότητα σε ένα σύστημα ανισοτήτων.

2. Αποδεικνύεται ομοίως ότι

Ας γράψουμε αυτά τα διαγράμματα στον πίνακα αναφοράς. Σκεφτείτε τις αποδείξεις τύπου 3 και 4 στο σπίτι, θα τις συζητήσουμε στο επόμενο μάθημα.

VI.Ας λύσουμε την ανισότητα με έναν νέο τρόπο.

Η αρχική ανισότητα είναι ισοδύναμη με ένα σύνολο συστημάτων.

VII.Και υπάρχει μια τρίτη μέθοδος που συχνά βοηθά στην επίλυση πολύπλοκων παράλογων ανισοτήτων. Έχουμε ήδη μιλήσει για αυτό σε σχέση με ανισότητες με συντελεστή. το μέθοδος αντικατάστασης συνάρτησης (αντικατάσταση πολλαπλασιαστή). Επιτρέψτε μου να σας υπενθυμίσω ότι η ουσία της μεθόδου αντικατάστασης είναι ότι η διαφορά στις τιμές των μονοτονικών συναρτήσεων μπορεί να αντικατασταθεί από τη διαφορά στις τιμές των ορισμάτων τους.

Σκεφτείτε μια παράλογη ανισότητα της μορφής<,

αυτό είναι -< 0.

Θεωρητικά, αν p(x)αυξάνεται σε κάποιο διάστημα στο οποίο ανήκουν ένακαι σι, και ένα>σι, μετά οι ανισότητες p(a) – p(b) > 0 και α-β> 0 ισοδυναμούν με D(p), αυτό είναι

VIII.Επιλύουμε την ανισότητα με τη μέθοδο των μεταβαλλόμενων παραγόντων.

Επομένως, αυτή η ανισότητα είναι ισοδύναμη με το σύστημα

Έτσι, είδαμε ότι η χρήση της μεθόδου αντικατάστασης παραγόντων για τη μείωση της λύσης μιας ανισότητας στη μέθοδο των διαστημάτων μειώνει σημαντικά την ποσότητα εργασίας.

IX.Τώρα που καλύψαμε τις τρεις βασικές μεθόδους για την επίλυση εξισώσεων, ας το κάνουμε ανεξάρτητη εργασία με αυτοεξέταση.

Είναι απαραίτητο να εκτελέσετε τους ακόλουθους αριθμούς (σύμφωνα με το εγχειρίδιο του A. M. Mordkovich): 1790 (α) - λύστε_ με τη μέθοδο_ ισοδύναμων μεταβάσεων,_ 1791 (α) - επίλυση με τη μέθοδο αντικατάστασης παραγόντων. Για επίλυση παράλογων ανισοτήτων, προτείνεται να χρησιμοποιηθούν οι μέθοδοι που αναλύθηκαν προηγουμένως κατά την επίλυση παράλογων εξισώσεων:

• αλλαγή μεταβλητών?
• χρήση ODZ.
• χρήση ιδιοτήτων μονοτονίας συναρτήσεων.

Η ολοκλήρωση της μελέτης του θέματος είναι τεστ.

Η ανάλυση της εργασίας ελέγχου δείχνει:

• Τα τυπικά λάθη των αδύναμων μαθητών, εκτός από τα αριθμητικά και τα αλγεβρικά, είναι εσφαλμένες ισοδύναμες μεταβάσεις σε ένα σύστημα ανισοτήτων.
• η μέθοδος υποκατάστασης παραγόντων χρησιμοποιείται με επιτυχία μόνο από δυνατούς μαθητές.

T.D. Ιβάνοβα

ΜΕΘΟΔΟΙ ΕΠΙΛΥΣΗΣ ΠΑΡΑΟΡΘΩΝ ΑΝΙΣΟΤΗΤΩΝ

CDO και NIT SRPTL

UDC 511 (O75.3)

BBC 22. 1Y72

Συντάχθηκε από την T.D. Ivanova

Κριτής: Baisheva M.I.– Υποψήφιος Παιδαγωγικών Επιστημών, Αναπληρωτής Καθηγητής του Τμήματος

Μαθηματική Ανάλυση Μαθηματική Σχολή

Ινστιτούτο Μαθηματικών και Πληροφορικής του Γιακούτσκ

κρατικό Πανεπιστήμιο

Μέθοδοι επίλυσης παράλογων ανισοτήτων: Μεθοδολογικός οδηγός

M 34 για μαθητές των τάξεων 9-11 / συζ. Ivanova T.D. από το Suntar Suntarsky ulus

RS (Y): TsDO NIT SRPTL, 2007, - 56 p.

Το εγχειρίδιο απευθύνεται σε μαθητές γυμνασίου δευτεροβάθμιας εκπαίδευσης, καθώς και σε όσους εισέρχονται σε πανεπιστήμια ως μεθοδολογικός οδηγός για την επίλυση παράλογων ανισοτήτων. Το εγχειρίδιο αναλύει λεπτομερώς τις κύριες μεθόδους για την επίλυση παράλογων ανισοτήτων, δίνει παραδείγματα επίλυσης παράλογων ανισοτήτων με παραμέτρους και προσφέρει επίσης παραδείγματα για μια ανεξάρτητη λύση. Οι εκπαιδευτικοί μπορούν να χρησιμοποιήσουν το εγχειρίδιο ως διδακτικό υλικό για ανεξάρτητη εργασία, με επισκόπηση επανάληψης του θέματος «Παράλογες ανισότητες».

Το εγχειρίδιο αντικατοπτρίζει την εμπειρία του δασκάλου στη μελέτη του θέματος «Παράλογες ανισότητες» με τους μαθητές.

Οι εργασίες προέρχονται από το υλικό των εισαγωγικών εξετάσεων, μεθοδικές εφημερίδες και περιοδικά, σχολικά βιβλία, ο κατάλογος των οποίων δίνεται στο τέλος του εγχειριδίου

UDC 511 (O75.3)

BBC 22. 1Y72

 T.D. Ivanova, σύντ., 2006.

 CDO NIT SRPTL, 2007.

Πρόλογος 5

Εισαγωγή 6

Ενότητα Ι. Παραδείγματα επίλυσης των απλούστερων παράλογων ανισώσεων 7

Ενότητα ΙΙ. Ανισότητες της μορφής
>g(x), g(x), g(x) 9

Ενότητα III. Ανισότητες της μορφής
;
;

;
13

Ενότητα IV. Ανισώσεις που περιέχουν πολλές ζυγές ρίζες 16

Ενότητα V. Μέθοδος αντικατάστασης (εισαγωγή νέας μεταβλητής) 20

Ενότητα VI. Ανισώσεις της μορφής f(x)
0; f(x)0;

Ενότητα VII. Ανισότητες της μορφής
25

Ενότητα VIII. Χρήση ριζικών μετασχηματισμών

σε παράλογες ανισότητες 26

Ενότητα IX. Γραφική επίλυση παράλογων ανισοτήτων 27

Ενότητα Χ. Ανισώσεις μικτού τύπου 31

Ενότητα XI. Χρησιμοποιώντας την ιδιότητα μονοτονίας μιας συνάρτησης 41

Ενότητα XII. Μέθοδος αντικατάστασης λειτουργίας 43

Ενότητα XIII. Παραδείγματα άμεσης επίλυσης ανισοτήτων

Μέθοδος διαστήματος 45

Ενότητα XIV. Παραδείγματα επίλυσης παράλογων ανισοτήτων με παραμέτρους 46

Λογοτεχνία 56

ΑΝΑΣΚΟΠΗΣΗ

Αυτό το εγχειρίδιο προορίζεται για μαθητές των τάξεων 10-11. Όπως δείχνει η πρακτική, οι μαθητές, οι αιτούντες αντιμετωπίζουν ιδιαίτερες δυσκολίες στην επίλυση παράλογων ανισοτήτων. Αυτό οφείλεται στο γεγονός ότι στα σχολικά μαθηματικά αυτή η ενότητα θεωρείται ανεπαρκώς, διάφορες μέθοδοι για την επίλυση τέτοιων ανισοτήτων δεν εξετάζονται εκτενέστερα. Οι δάσκαλοι των σχολείων αισθάνονται επίσης έλλειψη μεθοδολογικής βιβλιογραφίας, η οποία εκδηλώνεται σε περιορισμένο όγκο υλικού εργασίας που υποδεικνύει διάφορες προσεγγίσεις και μεθόδους επίλυσης.

Το εγχειρίδιο εξετάζει μεθόδους για την επίλυση παράλογων ανισοτήτων. Ivanova T.D. στην αρχή κάθε ενότητας εισάγει τους μαθητές στην κύρια ιδέα της μεθόδου, στη συνέχεια παρουσιάζονται παραδείγματα με επεξηγήσεις και προτείνονται εργασίες για ανεξάρτητη λύση.

Ο μεταγλωττιστής χρησιμοποιεί τις πιο «θεαματικές» μεθόδους για την επίλυση παράλογων ανισοτήτων που εμφανίζονται κατά την είσοδο σε ανώτατα εκπαιδευτικά ιδρύματα με αυξημένες απαιτήσεις για τις γνώσεις των μαθητών.

Οι μαθητές, έχοντας διαβάσει αυτό το εγχειρίδιο, μπορούν να αποκτήσουν ανεκτίμητη εμπειρία και δεξιότητες στην επίλυση περίπλοκων παράλογων ανισοτήτων. Πιστεύω ότι αυτό το εγχειρίδιο θα είναι χρήσιμο και σε καθηγητές μαθηματικών που εργάζονται σε εξειδικευμένες τάξεις, καθώς και σε προγραμματιστές μαθημάτων επιλογής.

Υποψήφιος Παιδαγωγικών Επιστημών, Αναπληρωτής Καθηγητής, Τμήμα Μαθηματικής Ανάλυσης, Μαθηματική Σχολή, Ινστιτούτο Μαθηματικών και Πληροφορικής, Κρατικό Πανεπιστήμιο Yakut

Baisheva M.I.

ΠΡΟΛΟΓΟΣ

Το εγχειρίδιο απευθύνεται σε μαθητές γυμνασίου δευτεροβάθμιας εκπαίδευσης, καθώς και σε όσους εισέρχονται σε πανεπιστήμια ως μεθοδολογικός οδηγός για την επίλυση παράλογων ανισοτήτων. Το εγχειρίδιο αναλύει λεπτομερώς τις κύριες μεθόδους για την επίλυση παράλογων ανισοτήτων, δίνει υποδειγματικά μοτίβα για την επίλυση παράλογων ανισοτήτων, δίνει παραδείγματα επίλυσης παράλογων ανισοτήτων με παραμέτρους και προσφέρει επίσης παραδείγματα για μια ανεξάρτητη λύση, για ορισμένες από αυτές δίνονται σύντομες απαντήσεις και οδηγίες.

Κατά την ανάλυση παραδειγμάτων, επιλύοντας ανεξάρτητα ανισώσεις, θεωρείται ότι ο μαθητής είναι σε θέση να λύσει γραμμικές, τετράγωνες και άλλες ανισώσεις, κατέχει διάφορες μεθόδους για την επίλυση ανισώσεων, ιδίως τη μέθοδο των διαστημάτων. Προτείνεται η επίλυση της ανισότητας με διάφορους τρόπους.

Οι εκπαιδευτικοί μπορούν να χρησιμοποιήσουν το εγχειρίδιο ως διδακτικό υλικό για ανεξάρτητη εργασία, με επισκόπηση επανάληψης του θέματος «Παράλογες ανισότητες».

Το εγχειρίδιο αντικατοπτρίζει την εμπειρία του δασκάλου στη μελέτη του θέματος «Παράλογες ανισότητες» με τους μαθητές.

Οι εργασίες επιλέγονται από το υλικό των εισαγωγικών εξετάσεων στα ανώτατα εκπαιδευτικά ιδρύματα, τις μεθοδολογικές εφημερίδες και τα μαθηματικά περιοδικά "Πρώτη Σεπτεμβρίου", "Μαθηματικά στο σχολείο", "Quantum", σχολικά βιβλία, μια λίστα των οποίων δίνεται στο τέλος του εγχειριδίου .

ΕΙΣΑΓΩΓΗ

Παράλογες είναι οι ανισότητες στις οποίες οι μεταβλητές ή μια συνάρτηση μιας μεταβλητής μπαίνουν κάτω από το πρόσημο της ρίζας.

Η κύρια τυπική μέθοδος για την επίλυση παράλογων ανισοτήτων είναι η διαδοχική αύξηση και των δύο τμημάτων της ανισότητας σε μια ισχύ προκειμένου να απαλλαγούμε από τη ρίζα. Όμως αυτή η επέμβαση συχνά οδηγεί στην εμφάνιση ξένων ριζών ή ακόμα και στην απώλεια ριζών, δηλ. οδηγεί σε μια ανισότητα που δεν είναι ισοδύναμη με την αρχική. Επομένως, είναι απαραίτητο να παρακολουθείται προσεκτικά η ισοδυναμία των μετασχηματισμών και να λαμβάνονται υπόψη μόνο εκείνες οι τιμές της μεταβλητής για τις οποίες έχει νόημα η ανισότητα:

αν η ρίζα είναι άρτιας βαθμίδας, τότε η ριζική έκφραση πρέπει να είναι μη αρνητική και η τιμή της ρίζας πρέπει επίσης να είναι μη αρνητικός αριθμός.

αν η ρίζα του βαθμού είναι περιττός αριθμός, τότε η ριζική έκφραση μπορεί να πάρει οποιονδήποτε πραγματικό αριθμό και το πρόσημο της ρίζας συμπίπτει με το πρόσημο της ριζικής έκφρασης.

Είναι δυνατό να αυξήσετε και τα δύο μέρη της ανισότητας σε άρτια ισχύ μόνο αφού πρώτα βεβαιωθείτε ότι είναι μη αρνητικά.

Η αύξηση και των δύο πλευρών μιας ανισότητας στην ίδια περιττή δύναμη είναι πάντα ένας ισοδύναμος μετασχηματισμός.

ΚεφάλαιοΕγώ. Παραδείγματα επίλυσης των απλούστερων παράλογων ανισοτήτων

Παραδείγματα 1- 6:

Λύση:

1. α)
.

σι)
.

2. α)

σι)

3. α)
.

σι)
.

4. α)

σι)

5. α)
.

σι)

6. α)
.

σι)
.

7.

8. α)
.

σι)

9. α)
.

σι)

11.

12. Να βρείτε τον μικρότερο θετικό ακέραιο x που ικανοποιεί την ανίσωση

13. α) Να βρείτε το μέσο του διαστήματος λύσης της ανίσωσης

β) Να βρείτε τον αριθμητικό μέσο όρο όλων των ακέραιων τιμών του x για τις οποίες η ανίσωση έχει λύση 4

14. Να βρείτε τη μικρότερη αρνητική λύση της ανίσωσης

15. α)
;

σι)

Ενότητα II. Ανισώσεις της μορφής >g(x), g(x),g(x)

Ομοίως, όπως και στην επίλυση των παραδειγμάτων 1-4, επιχειρηματολογούμε όταν λύνουμε ανισώσεις του υποδεικνυόμενου τύπου.

Παράδειγμα 7 : Λύστε την ανισότητα
> Χ + 1

Λύση: Ανισότητες OHS: Χ-3. Για τη δεξιά πλευρά, υπάρχουν δύο πιθανές περιπτώσεις:

ένα) Χ+ 10 (η δεξιά πλευρά είναι μη αρνητική) ή β) Χ + 1

Σκεφτείτε α) Αν Χ+10, δηλ. Χ- 1, τότε και τα δύο μέρη της ανισότητας είναι μη αρνητικά. Ας τετραγωνίσουμε και τις δύο πλευρές: Χ + 3 >Χ+ 2Χ+ 1. Παίρνουμε την τετραγωνική ανισότητα Χ+ Χ – 2 Χ x - 1, παίρνουμε -1

Θεωρήστε β) Αν Χ+1 x x -3

Συνδυάζοντας τις λύσεις της περίπτωσης α) -1 και β) Χ-3, γράψε την απάντηση: Χ
.

Είναι βολικό να γράψετε όλα τα ορίσματα για την επίλυση του Παραδείγματος 7 ως εξής:

Η αρχική ανισότητα είναι ισοδύναμη με το σύνολο των συστημάτων ανισοτήτων
.

Χ

Απάντηση: .

Συλλογισμός κατά την επίλυση ανισώσεων της μορφής

1.> σολ(Χ); 2. σολ(Χ); 3. σολ(Χ); 4. σολ(Χ) μπορεί να γραφτεί εν συντομία ως τα ακόλουθα διαγράμματα:

ΕΓΩ. > σολ(Χ)

2. σολ(Χ)

3. σολ(Χ)

4. σολ(Χ)
.

Παράδειγμα 8 :
Χ.

Λύση: Η αρχική ανισότητα είναι ισοδύναμη με το σύστημα

x>0

Απάντηση: Χ
.

Εργασίες για ανεξάρτητη λύση:

σι)

σι)
.

σι)

σι)

20. α)
Χ

σι)

21. α)

Οποιαδήποτε ανισότητα, που περιλαμβάνει μια συνάρτηση κάτω από τη ρίζα, ονομάζεται παράλογος. Υπάρχουν δύο τύποι τέτοιων ανισοτήτων:

Στην πρώτη περίπτωση, η ρίζα είναι μικρότερη από τη συνάρτηση g (x), στη δεύτερη - περισσότερο. Αν g(x) - συνεχής, η ανισότητα απλοποιείται δραματικά. Σημειώστε ότι εξωτερικά αυτές οι ανισότητες είναι πολύ παρόμοιες, αλλά τα σχήματα επίλυσής τους είναι θεμελιωδώς διαφορετικά.

Σήμερα θα μάθουμε πώς να λύνουμε παράλογες ανισότητες του πρώτου τύπου - είναι οι πιο απλές και κατανοητές. Το σύμβολο της ανισότητας μπορεί να είναι αυστηρό ή μη. Η ακόλουθη δήλωση ισχύει για αυτούς:

Θεώρημα. Κάθε παράλογη ανισότητα της μορφής

Ισοδυναμεί με το σύστημα των ανισοτήτων:

Δεν είναι αδύναμο; Ας δούμε από πού προέρχεται ένα τέτοιο σύστημα:

1. f (x) ≤ g 2 (x) - όλα είναι ξεκάθαρα εδώ. Αυτή είναι η αρχική ανισότητα στο τετράγωνο.
2. f(x) ≥ 0 είναι το ODZ της ρίζας. Να σας θυμίσω: η αριθμητική τετραγωνική ρίζα υπάρχει μόνο από μη αρνητικόαριθμοί?
3. g(x) ≥ 0 είναι το εύρος της ρίζας. Τετραγωνίζοντας την ανισότητα, καίμε τα μειονεκτήματα. Ως αποτέλεσμα, μπορεί να εμφανιστούν επιπλέον ρίζες. Η ανισότητα g (x) ≥ 0 τα κόβει.

Πολλοί μαθητές «πάνε σε κύκλους» στην πρώτη ανισότητα του συστήματος: f (x) ≤ g 2 (x) - και ξεχνάνε τελείως τις άλλες δύο. Το αποτέλεσμα είναι προβλέψιμο: λάθος απόφαση, χαμένοι βαθμοί.

Δεδομένου ότι οι παράλογες ανισότητες είναι ένα αρκετά περίπλοκο θέμα, ας αναλύσουμε 4 παραδείγματα ταυτόχρονα. Από στοιχειώδες έως πραγματικά πολύπλοκο. Όλες οι εργασίες λαμβάνονται από τις εισαγωγικές εξετάσεις του Κρατικού Πανεπιστημίου της Μόσχας. M. V. Lomonosov.

Παραδείγματα επίλυσης προβλημάτων

Μια εργασία. Λύστε την ανισότητα:

Έχουμε ένα κλασικό παράλογη ανισότητα: f(x) = 2x + 3; g(x) = 2 είναι σταθερά. Εχουμε:

Μόνο δύο από τις τρεις ανισότητες παρέμειναν μέχρι το τέλος της λύσης. Επειδή η ανίσωση 2 ≥ 0 ισχύει πάντα. Ας τέμνουμε τις υπόλοιπες ανισότητες:

Άρα, x ∈ [−1,5; 0,5]. Όλα τα σημεία είναι σκιασμένα γιατί οι ανισότητες δεν είναι αυστηρές.

Μια εργασία. Λύστε την ανισότητα:

Εφαρμόζουμε το θεώρημα:

Λύνουμε την πρώτη ανισότητα. Για να γίνει αυτό, θα ανοίξουμε το τετράγωνο της διαφοράς. Εχουμε:

2x 2 − 18x + 16< (x − 4) 2 ;
2x 2 − 18x + 16< x 2 − 8x + 16:
x 2 − 10x< 0;
x (x − 10)< 0;
x ∈ (0; 10).

Τώρα ας λύσουμε τη δεύτερη ανισότητα. Εκεί επίσης τετράγωνο τριώνυμο:

2x 2 − 18x + 16 ≥ 0;
x 2 − 9x + 8 ≥ 0;
(x − 8)(x − 1) ≥ 0;
x ∈ (−∞; 1]∪∪∪∪)