|
Prima limită remarcabilă. Derivarea primei limite remarcabile este de interes din punct de vedere al aplicării teoriei limitelor și de aceea ți-o oferim aproape în întregime. Să luăm în considerare comportamentul funcției |
la 
. Pentru a face acest lucru, luați în considerare un cerc cu raza 1; să notăm unghiul central al MOB prin X, în care 
.Apoi în mod clar zona DMOA< площадь сектора МОА < площадьDСОА (см. рис. 1).
S D MOA = 
S MOA = 
=
S D C OA = 
Revenind la inegalitatea menționată și dublând-o, obținem:
păcat X < X < tg X.
După împărţirea pe termen sin X:
sau 
Deoarece 
, apoi variabila 
se incheie intre doua marimi care au aceeasi limita, i.e. , pe baza teoremei privind limita funcției intermediare din paragraful anterior, avem:
-prima limită minunată .
Exemplu. Calculați limitele funcțiilor folosind prima limită remarcabilă:
Răspuns. 1) 1, 2) 0, 3)
Exercițiu: Calculați limita unei funcții folosind prima limită remarcabilă:
Raspuns: -2.
A doua limită remarcabilă.
Pentru a deriva a doua limită remarcabilă, introducem definiția numărului e:
Definiție.
Limită variabilă 
la 
numit un număre
:
- A doua limită minunată
Număr e- număr irațional. Valoarea sa la zece zecimale adevărate este de obicei rotunjită la o zecimală adevărată:
e= 2,7182818284..."2,7.
Teorema. Funcţie 
laX
tinde spre infinit, tinde spre limităe
:
Exemplu. Calculați limitele funcțiilor:
Soluţie.
Conform proprietăților limitelor, limita gradului este egală cu gradul limitei, adică:
Mai mult, într-un mod similar se poate dovedi că 
Răspuns. 1)e 3 , 2)e 2 , 3)e 4 .
Exercițiu. Calculați limita funcției folosind a doua limită remarcabilă:
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
DESPRE 
răspuns: e -5
Continuitatea unei funcții Continuitatea unei funcții într-un punct
Definiție. Funcţief ( X ), X Î ( A ; b ) X O Î ( A ; b ), dacă limita funcţieif ( X ) la punctX O există și este egală cu valoarea funcției în acest moment:
.
Conform acestei definiții, continuitatea funcției f(X) la punct X Oînseamnă că sunt îndeplinite următoarele condiții:
funcţie f(X) trebuie definit la punct X O ;
funcția y f(X) trebuie să existe o limită la punct X O ;
limita unei funcții f(X) la punct X O trebuie să se potrivească cu valoarea funcției în acest moment.
Exemplu.
Funcţie f(X)
=
X 2
definite pe întreaga dreaptă numerică și continuă într-un punct X= 1 deoarece f( 1)
= 1 și 
Continuitatea unei funcții pe un set
Definiție. Funcţief(x), se numeste continuu pe interval(a; b), dacă este continuă în fiecare punct al acestui interval.
Dacă o funcție este continuă la un moment dat, atunci acest punct se numește punctul de continuitate al acestei funcții. În cazurile în care limita unei funcții într-un punct dat nu există sau valoarea acesteia nu coincide cu valoarea funcției într-un punct dat, atunci funcția se numește discontinuă în acest punct, iar punctul însuși se numește discontinuitate. punct al funcției f(x).
Proprietățile funcțiilor continue.
1) Suma unui număr finit de funcții continue într-un punct A,
2) Produsul unui număr finit de funcții continue într-un punct A, există o funcție care este continuă în acest punct.
3) Raportul unui număr finit de funcții continue într-un punct A, este o funcție care este continuă în acest punct dacă valoarea funcției din numitor este diferită de zero în acest punct A.
Exemplu.
Funcţie f(X) = X P, Unde n Î N, este continuă pe întreaga linie numerică. Acest fapt poate fi demonstrat folosind proprietatea 2 și continuitatea funcției f(X) = X.
Funcţie f(X) = sX P (Cu– constantă) este continuă pe întreaga dreaptă numerică, pe baza proprietății 2 și exemplului 1.
Teorema 1. Un polinom este o funcție care este continuă pe întreaga dreaptă numerică.
Teorema 2 . Orice funcție rațională fracțională este continuă în fiecare punct al domeniului său de definiție.
Exemplu.
Definiție
Funcţief
(
X
)
numit continuu intr-un punctx = a
, dacă în acest moment crește 
tinde spre zero atunci când argumentul crește 
tinde spre zero, sau cu alte cuvinte: funcțief
(X)
numit continuu intr-un punctx = a
, dacă în acest moment un increment infinitezimal al argumentului corespunde unui increment infinitezimal al funcției, adică dacă 
Există mai multe limite remarcabile, dar cele mai cunoscute sunt prima și a doua limite remarcabile. Lucrul remarcabil la aceste limite este că sunt utilizate pe scară largă și cu ajutorul lor se pot găsi și alte limite întâlnite în numeroase probleme. Aceasta este ceea ce vom face în partea practică a acestei lecții. Pentru a rezolva probleme reducându-le la prima sau a doua limită remarcabilă, nu este nevoie să dezvăluie incertitudinile conținute în ele, deoarece valorile acestor limite au fost deduse mult timp de marii matematicieni.
Prima limită remarcabilă se numește limita raportului dintre sinusul unui arc infinitezimal și același arc, exprimat în radiani:
Să trecem la rezolvarea problemelor la prima limită remarcabilă. Notă: dacă există o funcție trigonometrică sub semnul limită, acesta este un semn aproape sigur că această expresie poate fi redusă la prima limită remarcabilă.
Exemplul 1. Găsiți limita.
Soluţie. Înlocuire în schimb X zero duce la incertitudine:
.
Numitorul este sinus, prin urmare, expresia poate fi adusă la prima limită remarcabilă. Să începem transformarea:
.
Numitorul este sinusul a trei X, dar numărătorul are doar un X, ceea ce înseamnă că trebuie să obțineți trei X la numărător. Pentru ce? A introduce 3 X = Ași obțineți expresia .
Și ajungem la o variație a primei limite remarcabile:
pentru că nu contează ce literă (variabilă) din această formulă este în locul lui X.
Înmulțim X cu trei și împărțim imediat:
.
În conformitate cu prima limită remarcabilă observată, înlocuim expresia fracțională:
Acum putem rezolva în sfârșit această limită:
.
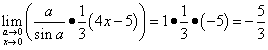Exemplul 2. Găsiți limita.
Soluţie. Substituția directă duce din nou la incertitudinea „zero împărțit la zero”:
.
Pentru a obține prima limită remarcabilă, este necesar ca x sub semnul sinus la numărător și doar x la numitor să aibă același coeficient. Fie acest coeficient egal cu 2. Pentru a face acest lucru, imaginați-vă coeficientul curent pentru x ca mai jos, efectuând operații cu fracții, obținem:
.
Exemplul 3. Găsiți limita.
Soluţie. Când înlocuim, obținem din nou incertitudinea „zero împărțit la zero”:
.
Probabil că deja înțelegeți că din expresia originală puteți obține prima limită minunată înmulțită cu prima limită minunată. Pentru a face acest lucru, descompunem pătratele lui x la numărător și sinusul la numitor în factori identici, iar pentru a obține aceiași coeficienți pentru x și sinus, împărțim x din numărător cu 3 și imediat înmulțim cu 3. Obținem:
.
Exemplul 4. Găsiți limita.
Soluţie. Din nou, obținem incertitudinea „zero împărțit la zero”:
.
Putem obține raportul dintre primele două limite remarcabile. Împărțim atât numărătorul cât și numitorul cu x. Apoi, astfel încât coeficienții pentru sinusuri și axe să coincidă, înmulțim x superior cu 2 și împărțim imediat cu 2 și înmulțim x inferior cu 3 și împărțim imediat cu 3. Obținem:
Exemplul 5. Găsiți limita.
Soluţie. Și din nou incertitudinea „zero împărțit la zero”:
Ne amintim din trigonometrie că tangenta este raportul dintre sinus și cosinus, iar cosinusul lui zero este egal cu unu. Efectuăm transformările și obținem:
.
Exemplul 6. Găsiți limita.
Soluţie. Funcția trigonometrică sub semnul unei limite sugerează din nou utilizarea primei limite remarcabile. O reprezentăm ca raportul dintre sinus și cosinus.
Prima limită remarcabilă este următoarea egalitate:
\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)
Deoarece pentru $\alpha\to(0)$ avem $\sin\alpha\to(0)$, se spune că prima limită remarcabilă dezvăluie o incertitudine de forma $\frac(0)(0)$. În general, în formula (1), în locul variabilei $\alpha$, orice expresie poate fi plasată sub semnul sinus și la numitor, atâta timp cât sunt îndeplinite două condiții:
- Expresiile de sub semnul sinus și din numitor tind simultan spre zero, adică. există incertitudinea formei $\frac(0)(0)$.
- Expresiile de sub semnul sinus și la numitor sunt aceleași.
Corolarele din prima limită remarcabilă sunt, de asemenea, adesea folosite:
\begin(equation) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(ecuație)
Unsprezece exemple sunt rezolvate pe această pagină. Exemplul nr. 1 este dedicat demonstrarii formulelor (2)-(4). Exemplele nr. 2, nr. 3, nr. 4 și nr. 5 conțin soluții cu comentarii detaliate. Exemplele nr. 6-10 conțin soluții practic fără comentarii, deoarece explicațiile detaliate au fost date în exemplele anterioare. Soluția folosește câteva formule trigonometrice care pot fi găsite.
Permiteți-mi să observ că prezența funcțiilor trigonometrice cuplate cu incertitudinea $\frac (0) (0)$ nu înseamnă neapărat aplicarea primei limite remarcabile. Uneori sunt suficiente transformări trigonometrice simple - de exemplu, vezi.
Exemplul nr. 1
Demonstrați că $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
a) Deoarece $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, atunci:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
Deoarece $\lim_(\alpha\to(0))\cos(0)=1$ și $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$, Acea:
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$
b) Să facem schimbarea $\alpha=\sin(y)$. Deoarece $\sin(0)=0$, atunci din condiția $\alpha\to(0)$ avem $y\to(0)$. În plus, există o vecinătate de zero în care $\arcsin\alpha=\arcsin(\sin(y))=y$, deci:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$
Egalitatea $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ a fost dovedită.
c) Să facem înlocuirea $\alpha=\tg(y)$. Deoarece $\tg(0)=0$, atunci condițiile $\alpha\to(0)$ și $y\to(0)$ sunt echivalente. În plus, există o vecinătate de zero în care $\arctg\alpha=\arctg\tg(y))=y$, prin urmare, pe baza rezultatelor punctului a), vom avea:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\la(0))\frac(y)(\tg(y)) =\lim_(y\la(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
Egalitatea $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ a fost dovedită.
Egalitățile a), b), c) sunt adesea folosite împreună cu prima limită remarcabilă.
Exemplul nr. 2
Calculați limita $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4) ( x+7))$.
Deoarece $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ și $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, i.e. si atat numaratorul cat si numitorul fractiei tind simultan spre zero, atunci aici avem de-a face cu o incertitudine de forma $\frac(0)(0)$, i.e. Terminat. În plus, este clar că expresiile de sub semnul sinus și din numitor coincid (adică și este satisfăcut):
Deci, ambele condiții enumerate la începutul paginii sunt îndeplinite. De aici rezultă că formula este aplicabilă, i.e. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7 ))=1$.
Răspuns: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.
Exemplul nr. 3
Găsiți $\lim_(x\to(0))\frac(\sin(9x))(x)$.
Deoarece $\lim_(x\to(0))\sin(9x)=0$ și $\lim_(x\to(0))x=0$, atunci avem de-a face cu o incertitudine de forma $\frac (0 )(0)$, adică Terminat. Cu toate acestea, expresiile de sub semnul sinus și din numitor nu coincid. Aici trebuie să ajustați expresia din numitor la forma dorită. Avem nevoie ca expresia $9x$ să fie la numitor, atunci va deveni adevărată. În esență, ne lipsește un factor de $9$ în numitor, care nu este atât de greu de introdus – doar înmulțiți expresia din numitor cu $9$. Desigur, pentru a compensa înmulțirea cu $9$, va trebui să împărțiți imediat la $9$:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$
Acum, expresiile de la numitor și de sub semnul sinus coincid. Ambele condiții pentru limita $\lim_(x\to(0))\frac(\sin(9x))(9x)$ sunt îndeplinite. Prin urmare, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. Și asta înseamnă că:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Răspuns: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Exemplul nr. 4
Găsiți $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.
Deoarece $\lim_(x\to(0))\sin(5x)=0$ și $\lim_(x\to(0))\tg(8x)=0$, aici avem de-a face cu incertitudinea formei $\frac(0)(0)$. Cu toate acestea, forma primei limite remarcabile este încălcată. Un numărător care conține $\sin(5x)$ necesită un numitor de $5x$. În această situație, cel mai simplu mod este să împărțiți numărătorul cu $5x$ și să înmulțiți imediat cu $5x$. În plus, vom efectua o operație similară cu numitorul, înmulțind și împărțind $\tg(8x)$ la $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
Reducând cu $x$ și luând constanta $\frac(5)(8)$ în afara semnului limită, obținem:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Rețineți că $\lim_(x\to(0))\frac(\sin(5x))(5x)$ îndeplinește pe deplin cerințele pentru prima limită remarcabilă. Pentru a găsi $\lim_(x\to(0))\frac(\tg(8x))(8x)$ se aplică următoarea formulă:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Răspuns: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Exemplul nr. 5
Găsiți $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.
Deoarece $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (rețineți că $\cos(0)=1$) și $\ lim_(x\to(0))x^2=0$, atunci avem de-a face cu incertitudinea de forma $\frac(0)(0)$. Totuși, pentru a aplica prima limită remarcabilă, ar trebui să scăpați de cosinusul din numărător, trecând la sinusuri (pentru a aplica apoi formula) sau tangente (pentru a aplica apoi formula). Acest lucru se poate face cu următoarea transformare:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$
Să revenim la limită:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$
Fracția $\frac(\sin^2(5x))(x^2)$ este deja apropiată de forma necesară pentru prima limită remarcabilă. Să lucrăm puțin cu fracția $\frac(\sin^2(5x))(x^2)$, ajustând-o la prima limită remarcabilă (rețineți că expresiile din numărător și sub sinus trebuie să se potrivească):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$
Să revenim la limita în cauză:
$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0) ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Răspuns: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Exemplul nr. 6
Găsiți limita $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.
Deoarece $\lim_(x\to(0))(1-\cos(6x))=0$ și $\lim_(x\to(0))(1-\cos(2x))=0$, atunci avem de-a face cu incertitudinea $\frac(0)(0)$. Să o dezvăluim cu ajutorul primei limite remarcabile. Pentru a face acest lucru, să trecem de la cosinus la sinusuri. Deoarece $1-\cos(2\alpha)=2\sin^2(\alpha)$, atunci:
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Trecând la sinusuri în limita dată, vom avea:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) = 9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Răspuns: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Exemplul nr. 7
Calculați limita $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ sub rezerva $\alpha\neq \ beta$.
Explicații detaliate au fost date mai devreme, dar aici pur și simplu observăm că din nou există incertitudine $\frac(0)(0)$. Să trecem de la cosinus la sinus folosind formula
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Folosind această formulă, obținem:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\dreapta| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta) )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x) \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$
Răspuns: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alfa^2)(2)$.
Exemplul nr. 8
Găsiți limita $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.
Deoarece $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (rețineți că $\sin(0)=\tg(0)=0$) și $\ lim_(x\to(0))x^3=0$, atunci aici avem de-a face cu incertitudinea de forma $\frac(0)(0)$. Să-l defalcăm după cum urmează:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1) ) =\frac(1)(2). $$
Răspuns: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Exemplul nr. 9
Găsiți limita $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.
Deoarece $\lim_(x\to(3))(1-\cos(x-3))=0$ și $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, atunci există incertitudinea formei $\frac(0)(0)$. Înainte de a trece la extinderea acesteia, este convenabil să faceți o schimbare de variabilă în așa fel încât noua variabilă să tinde spre zero (rețineți că în formule variabila $\alpha \to 0$). Cel mai simplu mod este introducerea variabilei $t=x-3$. Cu toate acestea, pentru comoditatea transformărilor ulterioare (acest beneficiu poate fi văzut în cursul soluției de mai jos), merită să faceți următoarea înlocuire: $t=\frac(x-3)(2)$. Remarc că ambele înlocuiri sunt aplicabile în acest caz, doar că a doua înlocuire vă va permite să lucrați mai puțin cu fracții. Din moment ce $x\la(3)$, atunci $t\la(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\dreapta| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Răspuns: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Exemplul nr. 10
Găsiți limita $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2)$.
Încă o dată avem de-a face cu incertitudinea $\frac(0)(0)$. Înainte de a trece la extinderea acesteia, este convenabil să faceți o schimbare de variabilă în așa fel încât noua variabilă să tindă spre zero (rețineți că în formule variabila este $\alpha\to(0)$). Cel mai simplu mod este să introduceți variabila $t=\frac(\pi)(2)-x$. Deoarece $x\la\frac(\pi)(2)$, atunci $t\la(0)$:
$$ \lim_(x\la\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\stânga|\frac(0)(0)\dreapta| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Răspuns: $\lim_(x\la\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.
Exemplul nr. 11
Găsiți limitele $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2) \ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
În acest caz nu trebuie să folosim prima limită minunată. Vă rugăm să rețineți că atât prima cât și a doua limită conțin numai funcții și numere trigonometrice. Adesea în exemple de acest fel este posibilă simplificarea expresiei situate sub semnul limită. Mai mult, după simplificarea și reducerea menționată mai sus a unor factori, incertitudinea dispare. Am dat acest exemplu doar cu un singur scop: să arăt că prezența funcțiilor trigonometrice sub semnul limită nu înseamnă neapărat utilizarea primei limite remarcabile.
Deoarece $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (rețineți că $\sin\frac(\pi)(2)=1$ ) și $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (permiteți-mi să vă reamintesc că $\cos\frac(\pi)(2)=0$), atunci avem care se ocupă de incertitudinea formei $\frac(0)(0)$. Totuși, asta nu înseamnă că va trebui să folosim prima limită minunată. Pentru a dezvălui incertitudinea, este suficient să luăm în considerare faptul că $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\la\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
Există o soluție similară în cartea de soluții a lui Demidovich (nr. 475). În ceea ce privește a doua limită, ca și în exemplele anterioare din această secțiune, avem o incertitudine de forma $\frac(0)(0)$. De ce apare? Apare deoarece $\tg\frac(2\pi)(3)=-\sqrt(3)$ și $2\cos\frac(2\pi)(3)=-1$. Folosim aceste valori pentru a transforma expresiile în numărător și numitor. Scopul acțiunilor noastre este de a nota suma în numărător și numitor ca produs. Apropo, adesea în cadrul unui tip similar este convenabil să se schimbe o variabilă, făcută în așa fel încât noua variabilă să tinde spre zero (vezi, de exemplu, exemplele nr. 9 sau nr. 10 de pe această pagină). Totuși, în acest exemplu nu are rost să înlocuiești, deși, dacă se dorește, înlocuirea variabilei $t=x-\frac(2\pi)(3)$ nu este dificil de implementat.
$$ \lim_(x\la\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ la\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\la\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$
După cum puteți vedea, nu a trebuit să aplicăm prima limită minunată. Desigur, puteți face acest lucru dacă doriți (vezi nota de mai jos), dar nu este necesar.
Care este soluția folosind prima limită remarcabilă? arată ascunde
Folosind prima limită remarcabilă obținem:
$$ \lim_(x\la\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ dreapta))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3)) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$
Răspuns: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\la\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.
Prima limită remarcabilă este adesea folosită pentru a calcula limitele care conțin sinus, arcsinus, tangentă, arctangentă și incertitudinile rezultate ale zero împărțit la zero.
Formulă
Formula pentru prima limită remarcabilă este: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$
Observăm că pentru $ \alpha\to 0 $ obținem $ \sin\alpha \to 0 $, astfel avem zerouri în numărător și numitor. Astfel, formula primei limite remarcabile este necesară pentru a releva incertitudinile $ \frac(0)(0) $.
Pentru a aplica formula, trebuie îndeplinite două condiții:
- Expresiile conținute în sinus și numitorul fracției sunt aceleași
- Expresiile din sinusul și numitorul unei fracții tind spre zero
Atenţie! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Deși expresiile de sub sinus și la numitor sunt aceleași, totuși $ 2x ^2+1 = 1 $, pentru $ x\la 0 $. A doua condiție nu este îndeplinită, așa că NU POȚI aplica formula!
Consecințe
Destul de rar în sarcini puteți vedea o primă limită minunată pură, în care puteți nota imediat răspunsul. În practică, totul pare puțin mai complicat, dar pentru astfel de cazuri va fi util să cunoaștem consecințele primei limite remarcabile. Datorită acestora, puteți calcula rapid limitele necesare.
$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$
$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$
Exemple de soluții
Să luăm în considerare prima limită remarcabilă, exemple ale soluției sale pentru calcularea limitelor care conțin funcții trigonometrice și incertitudine $ \bigg[\frac(0)(0)\bigg] $
| Exemplul 1 |
| Calculați $ \lim_(x\to 0) \frac(\sin2x)(4x) $ |
| Soluţie |
|
Să ne uităm la limită și să observăm că conține un sinus. Apoi, înlocuim $ x = 0 $ în numărător și numitor și obținem incertitudinea zero împărțit la zero: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)(0) ) $$ Deja două semne că trebuie să aplicăm o limită minunată, dar există o mică nuanță: nu putem aplica imediat formula, deoarece expresia de sub semnul sinus diferă de expresia din numitor. Și avem nevoie de ei să fie egali. Prin urmare, folosind transformări elementare ale numărătorului, îl vom transforma în $2x$. Pentru a face acest lucru, le vom scoate pe cele două din numitorul fracției ca factor separat. Arată astfel: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ Vă rugăm rețineți că la sfârșit $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ a fost obținut după formula. Dacă nu vă puteți rezolva problema, trimiteți-ne-o. Vom oferi o soluție detaliată. Veți putea vizualiza progresul calculului și veți obține informații. Acest lucru vă va ajuta să obțineți nota de la profesorul dvs. în timp util! |
| Răspuns |
| $$ \lim_(x\la 0) \frac(\sin2x)(4x) =\frac(1)(2) $$ |
| Exemplul 2 |
| Găsiți $ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ |
| Soluţie |
|
Ca întotdeauna, mai întâi trebuie să cunoașteți tipul de incertitudine. Dacă este zero împărțit la zero, atunci acordăm atenție prezenței unui sinus: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ Această incertitudine ne permite să folosim formula primei limite remarcabile, dar expresia de la numitor nu este egală cu argumentul sinusului? Prin urmare, formula nu poate fi aplicată „direct”. Este necesar să înmulțiți și să împărțiți fracția cu argumentul sinusului: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x -x^4)(x ^3+2x)) = $$ Acum notăm proprietățile limitelor: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x -x^4)\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ A doua limită se potrivește exact formulei și este egală la unu: $$ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x )(2x-x^4) = $$ Înlocuim din nou $ x = 0 $ într-o fracție și obținem incertitudinea $ \frac(0)(0) $. Pentru a o elimina, este suficient să scoateți $ x $ din paranteze și să-l reduceți cu: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2 )(2) = 1 $$ |
| Răspuns |
| $$ \lim_(x\la 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$ |
| Exemplul 4 |
| Calculați $ \lim_(x\to0) \frac(\sin2x)(tg3x) $ |
| Soluţie |
|
Să începem calculul cu înlocuirea $ x=0 $. Ca rezultat, obținem incertitudinea $ \frac(0)(0) $. Limita conține un sinus și o tangentă, care sugerează o posibilă desfășurare a situației folosind formula primei limite remarcabile. Să transformăm numărătorul și numitorul fracției într-o formulă și consecință: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Acum vedem că în numărător și numitor există expresii care se potrivesc formulei și consecințelor. Argumentul sinus și argumentul tangentei sunt aceleași pentru numitorii corespunzători $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$ |
| Răspuns |
| $$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$ |
Articolul: „Prima limită remarcabilă, exemple de soluții” a vorbit despre cazuri în care este indicat să se folosească această formulă și consecințele ei.
Acest articol: „A doua limită remarcabilă” este dedicat dezvăluirii în limitele incertitudinilor de forma:
$ \bigg[\frac(\infty)(\infty)\bigg]^\infty $ și $ ^\infty $.
De asemenea, astfel de incertitudini pot fi relevate folosind logaritmul funcției exponențiale, dar aceasta este o altă metodă de soluție, care va fi tratată într-un alt articol.
Formula și consecințele
Formulă a doua limită remarcabilă se scrie astfel: $$ \lim_(x \to \infty) \bigg (1+\frac(1)(x)\bigg)^x = e, \text( where ) e \approx 2.718 $$
Rezultă din formulă consecințe, care sunt foarte convenabile de utilizat pentru rezolvarea exemplelor cu limite: $$ \lim_(x \to \infty) \bigg (1 + \frac(k)(x) \bigg)^x = e^k, \text( unde ) k \in \mathbb(R) $$ $$ \lim_(x \to \infty) \bigg (1 + \frac(1)(f(x)) \bigg)^(f(x)) = e $ $ $$ \lim_(x \to 0) \bigg (1 + x \bigg)^\frac(1)(x) = e $$
Este de remarcat faptul că a doua limită remarcabilă nu poate fi aplicată întotdeauna unei funcții exponențiale, ci numai în cazurile în care baza tinde spre unitate. Pentru a face acest lucru, mai întâi calculați mental limita bazei și apoi trageți concluzii. Toate acestea vor fi discutate în soluții de exemplu.
Exemple de soluții
Să ne uităm la exemple de soluții folosind formula directă și consecințele acesteia. Vom analiza și cazurile în care formula nu este necesară. Este suficient să scrieți doar un răspuns gata.
| Exemplul 1 |
| Găsiți limita $ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) $ |
| Soluţie |
|
Să substituim infinitul în limită și să ne uităm la incertitudine: $$ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) = \bigg (\frac (\infty)(\infty)\bigg)^\infty $$ Să găsim limita bazei: $$ \lim_(x\to\infty) \frac(x+4)(x+3)= \lim_(x\to\infty) \frac(x(1+\frac) (4)() x)))(x(1+\frac(3)(x))) = 1 $$ Am obținut o bază egală cu unu, ceea ce înseamnă că putem aplica deja a doua limită remarcabilă. Pentru a face acest lucru, să ajustăm baza funcției la formula scăzând și adăugând una: $$ \lim_(x\to\infty) \bigg(1 + \frac(x+4)(x+3) - 1 \bigg)^(x+3) = \lim_(x\to\infty) \ bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = $$ Să ne uităm la al doilea corolar și să scriem răspunsul: $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ Dacă nu vă puteți rezolva problema, trimiteți-ne-o. Vom oferi o soluție detaliată. Veți putea vizualiza progresul calculului și veți obține informații. Acest lucru vă va ajuta să obțineți nota de la profesorul dvs. în timp util! |
| Răspuns |
| $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ |
| Exemplul 4 |
| Rezolvați limita $ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) $ |
| Soluţie |
|
Găsim limita bazei și vedem că $ \lim_(x\to\infty) \frac(3x^2+4)(3x^2-2) = 1 $, ceea ce înseamnă că putem aplica a doua limită remarcabilă. Conform planului standard, adunăm și scădem unul din baza gradului: $$ \lim_(x\la \infty) \bigg (1+\frac(3x^2+4)(3x^2-2)-1 \bigg) ^(3x) = \lim_(x\to \infty ) \bigg (1+\frac(6)(3x^2-2) \bigg) ^(3x) = $$ Ajustăm fracția la formula notei a 2-a. limită: $$ = \lim_(x\la \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(3x) = $$ Acum, să ajustăm gradul. Puterea trebuie să conțină o fracție egală cu numitorul bazei $ \frac(3x^2-2)(6) $. Pentru a face acest lucru, înmulțiți și împărțiți gradul cu acesta și continuați să rezolvați: $$ = \lim_(x\la \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(\frac(3x^2-2) (6) \cdot \frac(6)(3x^2-2)\cdot 3x) = \lim_(x\to \infty) e^(\frac(18x)(3x^2-2)) = $$ Limita situată în puterea la $ e $ este egală cu: $ \lim_(x\to \infty) \frac(18x)(3x^2-2) = 0 $. Așadar, continuând soluția avem: |
| Răspuns |
| $$ \lim_(x\la \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) = 1 $$ |
Să examinăm cazurile în care problema este similară cu cea de-a doua limită remarcabilă, dar poate fi rezolvată fără ea.
În articolul: „A doua limită remarcabilă: exemple de soluții” au fost analizate formula, consecințele acesteia și au fost prezentate tipuri comune de probleme pe această temă.
