Calculator de fracții conceput pentru calcularea rapidă a operațiunilor cu fracții, vă va ajuta să adăugați, înmulțiți, împărțiți sau scădeți cu ușurință fracții.
Școlarii moderni încep să studieze fracțiile deja în clasa a V-a, iar exercițiile cu acestea devin din ce în ce mai complicate în fiecare an. Termenii și cantitățile matematice pe care le învățăm la școală ne pot fi foarte rar folositori în viața de adult. Cu toate acestea, fracțiile, spre deosebire de logaritmi și puteri, se găsesc destul de des în viața de zi cu zi (măsurarea distanțelor, cântărirea mărfurilor etc.). Calculatorul nostru este conceput pentru operații rapide cu fracții.
Mai întâi, să definim ce sunt fracțiile și ce sunt acestea. Fracțiile sunt raportul dintre un număr și altul; este un număr format dintr-un număr întreg de fracții ale unei unități.
Tipuri de fracții:
- Comun
- Zecimal
- Amestecat
Exemplu fracții ordinare:
Valoarea de sus este numărătorul, cea de jos este numitorul. Linia ne arată că numărul de sus este divizibil cu numărul de jos. În locul acestui format de scriere, când liniuța este orizontală, puteți scrie diferit. Puteți pune o linie înclinată, de exemplu:
1/2, 3/7, 19/5, 32/8, 10/100, 4/1
zecimale sunt cele mai populare tipuri de fracții. Ele constau dintr-o parte întreagă și o parte fracțională, separate prin virgulă.
Exemplu de fracții zecimale:
0,2 sau 6,71 sau 0,125
Constă dintr-un număr întreg și o parte fracțională. Pentru a afla valoarea acestei fracții, trebuie să adăugați numărul întreg și fracția.
Exemplu de fracții mixte:

Calculatorul de fracții de pe site-ul nostru web poate efectua rapid orice operație matematică cu fracții online:
- Plus
- Scădere
- Multiplicare
- Divizia
Pentru a efectua calculul, trebuie să introduceți numere în câmpuri și să selectați o acțiune. Pentru fracții, trebuie să completați numărătorul și numitorul; este posibil ca numărul întreg să nu fie scris (dacă fracția este obișnuită). Nu uitați să faceți clic pe butonul „egal”.
Este convenabil ca calculatorul să ofere imediat procesul de rezolvare a unui exemplu cu fracții și nu doar un răspuns gata făcut. Datorită soluției detaliate puteți folosi acest material pentru a rezolva problemele școlare și pentru a stăpâni mai bine materialul acoperit.
Trebuie să efectuați exemplul de calcul:
După introducerea indicatorilor în câmpurile formularului, obținem:

Pentru a face propriul calcul, introduceți datele în formular.
Acum că am învățat cum să adunăm și să înmulțim fracții individuale, ne putem uita la mai multe desene complexe. De exemplu, ce se întâmplă dacă aceeași problemă implică adunarea, scăderea și înmulțirea fracțiilor?
În primul rând, trebuie să convertiți toate fracțiile în fracțiuni necorespunzătoare. Apoi efectuăm acțiunile necesare în mod succesiv - în aceeași ordine ca și pentru numerele obișnuite. Și anume:
- Exponentiarea se face mai intai - scapa de toate expresiile care contin exponenti;
- Apoi - împărțirea și înmulțirea;
- Ultimul pas este adunarea și scăderea.
Desigur, dacă în expresie există paranteze, ordinea operațiilor se schimbă - tot ce se află în paranteze trebuie numărat mai întâi. Și amintiți-vă despre fracțiile improprii: trebuie să evidențiați întreaga parte numai atunci când toate celelalte acțiuni au fost deja finalizate.
Să convertim toate fracțiile din prima expresie în cele improprii și apoi să efectuăm următorii pași:

Acum să găsim valoarea celei de-a doua expresii. Nu există fracții cu o parte întreagă, dar există paranteze, așa că mai întâi facem adunarea și abia apoi împărțirea. Rețineți că 14 = 7 · 2. Apoi:
În cele din urmă, luați în considerare al treilea exemplu. Există paranteze și un grad aici - este mai bine să le numărați separat. Având în vedere că 9 = 3 3, avem:
Atenție la ultimul exemplu. Pentru a ridica o fracție la o putere, trebuie să ridicați separat numărătorul la această putere și separat, numitorul.
Puteți decide altfel. Dacă ne amintim definiția unui grad, problema se va reduce la înmulțirea obișnuită a fracțiilor:
Fracții cu mai multe etaje
Până acum am considerat doar fracții „pure”, când numărătorul și numitorul sunt numere obișnuite. Acest lucru este destul de în concordanță cu definiția unei fracții numerice dată în prima lecție.
Dar dacă puneți un obiect mai complex la numărător sau numitor? De exemplu, o altă fracție numerică? Astfel de construcții apar destul de des, mai ales când se lucrează cu expresii lungi. Iată câteva exemple:
Există o singură regulă pentru a lucra cu fracții cu mai multe niveluri: trebuie să scapi de ele imediat. Îndepărtarea podelelor „în plus” este destul de simplă, dacă vă amintiți că slash înseamnă operația standard de divizare. Prin urmare, orice fracție poate fi rescrisă după cum urmează:
Folosind acest fapt și urmând procedura, putem reduce cu ușurință orice fracție cu mai multe etaje la una obișnuită. Aruncă o privire la exemple:
Sarcină. Convertiți fracțiile cu mai multe etaje în fracții obișnuite:
În fiecare caz, rescriem fracția principală, înlocuind linia de despărțire cu un semn de diviziune. De asemenea, amintiți-vă că orice număr întreg poate fi reprezentat ca o fracție cu numitorul 1. Adică 12 = 12/1; 3 = 3/1. Primim:

În ultimul exemplu, fracțiile au fost anulate înainte de înmulțirea finală.
Specificul lucrului cu fracții cu mai multe niveluri
Există o subtilitate în fracțiile cu mai multe niveluri care trebuie reținută întotdeauna, altfel puteți obține răspunsul greșit, chiar dacă toate calculele au fost corecte. Aruncă o privire:
- Numătorul este un singur număr 7, iar numitorul este fracția 12/5;
- Numătorul conține fracția 7/12, iar numitorul conține numărul separat 5.
Deci, pentru o înregistrare am primit două interpretări complet diferite. Dacă numărați, răspunsurile vor fi și ele diferite:
Pentru a vă asigura că înregistrarea este întotdeauna citită fără ambiguitate, utilizați o regulă simplă: linia de despărțire a fracției principale trebuie să fie mai lungă decât linia fracției imbricate. De preferat de mai multe ori.
Dacă urmați această regulă, atunci fracțiile de mai sus ar trebui scrise după cum urmează:
Da, probabil că este inestetic și ocupă prea mult spațiu. Dar vei număra corect. În cele din urmă, câteva exemple în care apar efectiv fracții cu mai multe etaje:
Sarcină. Găsiți semnificațiile expresiilor:
Deci, să lucrăm cu primul exemplu. Să convertim toate fracțiile în fracții improprii și apoi să efectuăm operații de adunare și împărțire:

Să facem același lucru cu al doilea exemplu. Să convertim toate fracțiile în fracții improprii și să efectuăm operațiile necesare. Pentru a nu plictisi cititorul, voi omite câteva calcule evidente. Avem:

Datorită faptului că numărătorul și numitorul fracțiilor de bază conțin sume, regula de scriere fracții cu mai multe etaje este observat automat. De asemenea, în ultimul exemplu, am lăsat intenționat 46/1 sub formă de fracție pentru a efectua împărțirea.
De asemenea, voi observa că în ambele exemple bara de fracțiuni înlocuiește de fapt parantezele: în primul rând, am găsit suma și abia apoi coeficientul.
Unii vor spune că trecerea la fracții improprii în al doilea exemplu a fost în mod clar redundantă. Poate că acest lucru este adevărat. Dar făcând acest lucru ne asigurăm împotriva greșelilor, pentru că data viitoare exemplul se poate dovedi mult mai complicat. Alegeți singur ceea ce este mai important: viteza sau fiabilitatea.
Acest articol examinează operațiunile pe fracții. Se vor forma și justifica reguli de adunare, scădere, înmulțire, împărțire sau exponențiere a fracțiilor de forma A B, unde A și B pot fi numere, expresii numerice sau expresii cu variabile. În concluzie, vor fi luate în considerare exemple de soluții cu descrieri detaliate.
Yandex.RTB R-A-339285-1
Reguli pentru efectuarea operaţiilor cu fracţii numerice generale
Fracții numerice vedere generala au un numărător și un numitor în care există numere întregi sau expresii numerice. Dacă luăm în considerare fracții precum 3 5, 2, 8 4, 1 + 2 3 4 (5 - 2), 3 4 + 7 8 2, 3 - 0, 8, 1 2 2, π 1 - 2 3 + π, 2 0, 5 ln 3, atunci este clar că numărătorul și numitorul pot avea nu numai numere, ci și expresii de diferite tipuri.
Definiția 1
Există reguli prin care se efectuează acțiuni fracții obișnuite. Este potrivit și pentru fracții generale:
- La scăderea fracțiilor cu numitori similari se adună doar numărătorii, iar numitorul rămâne același, și anume: a d ± c d = a ± c d, valorile a, c și d ≠ 0 sunt niște numere sau expresii numerice.
- La adunarea sau scăderea unei fracții cu numitori diferiți, este necesar să o reduceți la un numitor comun, apoi să adăugați sau scădeți fracțiile rezultate cu aceiași exponenți. Literal, arată astfel: a b ± c d = a · p ± c · r s, unde valorile a, b ≠ 0, c, d ≠ 0, p ≠ 0, r ≠ 0, s ≠ 0 sunt numere realeși b · p = d · r = s . Când p = d și r = b, atunci a b ± c d = a · d ± c · d b · d.
- La înmulțirea fracțiilor, acțiunea se realizează cu numărători, după care cu numitori, atunci obținem a b · c d = a · c b · d, unde a, b ≠ 0, c, d ≠ 0 acționează ca numere reale.
- Când împărțim o fracție la o fracție, o înmulțim pe prima cu a doua inversă, adică schimbăm numărătorul și numitorul: a b: c d = a b · d c.
Rațiunea regulilor
Definiția 2Există următoarele puncte matematice pe care ar trebui să te bazezi când calculezi:
- bara oblică înseamnă semnul de împărțire;
- împărțirea la un număr este tratată ca o înmulțire cu valoarea sa reciprocă;
- aplicarea proprietății operațiilor cu numere reale;
- aplicarea proprietății de bază a fracțiilor și a inegalităților numerice.
Cu ajutorul lor, puteți efectua transformări ale formei:
a d ± c d = a · d - 1 ± c · d - 1 = a ± c · d - 1 = a ± c d ; a b ± c d = a · p b · p ± c · r d · r = a · p s ± c · e s = a · p ± c · r s ; a b · c d = a · d b · d · b · c b · d = a · d · a · d - 1 · b · c · b · d - 1 = = a · d · b · c · b · d - 1 · b · d - 1 = a · d · b · c b · d · b · d - 1 = = (a · c) · (b · d) - 1 = a · c b · d
Exemple
În paragraful anterior s-a spus despre operații cu fracții. După aceasta, fracția trebuie simplificată. Acest subiect a fost discutat în detaliu în paragraful despre conversia fracțiilor.
Mai întâi, să ne uităm la un exemplu de adunare și scădere a fracțiilor cu același numitor.
Exemplul 1
Având în vedere fracțiile 8 2, 7 și 1 2, 7, atunci conform regulii este necesar să adăugați numărătorul și să rescrieți numitorul.
Soluţie
Apoi obținem o fracție de forma 8 + 1 2, 7. După efectuarea adunării, obținem o fracție de forma 8 + 1 2, 7 = 9 2, 7 = 90 27 = 3 1 3. Deci, 8 2, 7 + 1 2, 7 = 8 + 1 2, 7 = 9 2, 7 = 90 27 = 3 1 3.
Răspuns: 8 2 , 7 + 1 2 , 7 = 3 1 3
Există o altă soluție. Pentru început, trecem la forma unei fracții obișnuite, după care efectuăm o simplificare. Arata cam asa:
8 2 , 7 + 1 2 , 7 = 80 27 + 10 27 = 90 27 = 3 1 3
Exemplul 2
Să scădem din 1 - 2 3 · log 2 3 · log 2 5 + 1 o fracție de forma 2 3 3 · log 2 3 · log 2 5 + 1 .
Deoarece sunt dați numitori egali, înseamnă că calculăm o fracție cu același numitor. Înțelegem asta
1 - 2 3 log 2 3 log 2 5 + 1 - 2 3 3 log 2 3 log 2 5 + 1 = 1 - 2 - 2 3 3 log 2 3 log 2 5 + 1
Există exemple de calculare a fracțiilor cu numitori diferiți. Un punct important este reducerea la numitor comun. Fără aceasta, nu vom putea efectua alte operații cu fracții.
Procesul amintește vag de reducerea la un numitor comun. Adică se caută cel mai mic divizor comun din numitor, după care factorii lipsă se adaugă la fracții.
Dacă fracțiile adăugate nu au factori comuni, atunci produsul lor poate deveni unul.
Exemplul 3
Să ne uităm la exemplul de adunare a fracțiilor 2 3 5 + 1 și 1 2.
Soluţie
În acest caz, numitorul comun este produsul numitorilor. Atunci obținem că 2 · 3 5 + 1. Apoi, atunci când stabilim factori suplimentari, avem că pentru prima fracție este egală cu 2, iar pentru a doua este 3 5 + 1. După înmulțire, fracțiile sunt reduse la forma 4 2 · 3 5 + 1. Reducerea generală a lui 1 2 va fi 3 5 + 1 2 · 3 5 + 1. Adăugăm expresiile fracționale rezultate și obținem asta
2 3 5 + 1 + 1 2 = 2 2 2 3 5 + 1 + 1 3 5 + 1 2 3 5 + 1 = = 4 2 3 5 + 1 + 3 5 + 1 2 3 5 + 1 = 4 + 3 5 + 1 2 3 5 + 1 = 5 + 3 5 2 3 5 + 1
Răspuns: 2 3 5 + 1 + 1 2 = 5 + 3 5 2 3 5 + 1
Când avem de-a face cu fracții generale, atunci de obicei nu vorbim despre cel mai mic numitor comun. Este neprofitabil să luăm ca numitor produsul numărătorilor. Mai întâi trebuie să verificați dacă există un număr care are o valoare mai mică decât produsul lor.
Exemplul 4
Să luăm în considerare exemplul lui 1 6 · 2 1 5 și 1 4 · 2 3 5, când produsul lor este egal cu 6 · 2 1 5 · 4 · 2 3 5 = 24 · 2 4 5. Apoi luăm 12 · 2 3 5 ca numitor comun.
Să ne uităm la exemple de înmulțire a fracțiilor generale.
Exemplul 5
Pentru a face acest lucru, trebuie să înmulțiți 2 + 1 6 și 2 · 5 3 · 2 + 1.
Soluţie
Urmând regula, este necesar să rescrieți și să scrieți produsul numărătorilor ca numitor. Obținem că 2 + 1 6 2 5 3 2 + 1 2 + 1 2 5 6 3 2 + 1. Odată ce o fracție a fost înmulțită, puteți face reduceri pentru a o simplifica. Atunci 5 · 3 3 2 + 1: 10 9 3 = 5 · 3 3 2 + 1 · 9 3 10.
Folosind regula pentru trecerea de la împărțirea la înmulțirea cu o fracție reciprocă, obținem o fracție care este reciproca celei date. Pentru a face acest lucru, numărătorul și numitorul sunt schimbate. Să ne uităm la un exemplu:
5 3 3 2 + 1: 10 9 3 = 5 3 3 2 + 1 9 3 10
Apoi trebuie să înmulțească și să simplifice fracția rezultată. Dacă este necesar, scăpați de iraționalitatea în numitor. Înțelegem asta
5 3 3 2 + 1: 10 9 3 = 5 3 3 9 3 10 2 + 1 = 5 2 10 2 + 1 = 3 2 2 + 1 = 3 2 - 1 2 2 + 1 2 - 1 = 3 2 - 1 2 2 2 - 1 2 = 3 2 - 1 2
Răspuns: 5 3 3 2 + 1: 10 9 3 = 3 2 - 1 2
Acest paragraf este aplicabil atunci când un număr sau o expresie numerică poate fi reprezentat ca o fracție cu un numitor egal cu 1, atunci operația cu o astfel de fracție este considerată un paragraf separat. De exemplu, expresia 1 6 · 7 4 - 1 · 3 arată că rădăcina lui 3 poate fi înlocuită cu o altă expresie 3 1. Atunci această intrare va arăta ca înmulțirea a două fracții de forma 1 6 · 7 4 - 1 · 3 = 1 6 · 7 4 - 1 · 3 1.
Efectuarea de operații asupra fracțiilor care conțin variabile
Regulile discutate în primul articol sunt aplicabile operațiilor cu fracții care conțin variabile. Luați în considerare regula scăderii atunci când numitorii sunt aceiași.
Este necesar să se demonstreze că A, C și D (D nu este egal cu zero) pot fi orice expresii, iar egalitatea A D ± C D = A ± C D este echivalentă cu domeniul său de valori admisibile.
Este necesar să se ia un set de variabile ODZ. Atunci A, C, D trebuie să ia valorile corespunzătoare a 0 , c 0 și d 0. Înlocuirea formei A D ± C D are ca rezultat o diferență de forma a 0 d 0 ± c 0 d 0 , unde, folosind regula adunării, obținem o formulă de forma a 0 ± c 0 d 0 . Dacă înlocuim expresia A ± C D, atunci obținem aceeași fracție de forma a 0 ± c 0 d 0. De aici concluzionăm că valoarea selectată care satisface ODZ, A ± C D și A D ± C D sunt considerate egale.
Pentru orice valoare a variabilelor, aceste expresii vor fi egale, adică se numesc identic egale. Aceasta înseamnă că această expresie este considerată o egalitate demonstrabilă de forma A D ± C D = A ± C D .
Exemple de adunare și scădere de fracții cu variabile
Când aveți aceiași numitori, trebuie doar să adăugați sau să scădeți numărătorii. Această fracție poate fi simplificată. Uneori trebuie să lucrați cu fracții care sunt identic egale, dar la prima vedere acest lucru nu se observă, deoarece unele transformări trebuie efectuate. De exemplu, x 2 3 x 1 3 + 1 și x 1 3 + 1 2 sau 1 2 sin 2 α și sin a cos a. Cel mai adesea, este necesară o simplificare a expresiei originale pentru a vedea aceiași numitori.
Exemplul 6
Calculați: 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2, 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) , x - 1 x - 1 + x x + 1 .
Soluţie
- Pentru a face calculul, trebuie să scădeți fracțiile care au același numitor. Atunci obținem că x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + 1 - 5 - x x + x - 2 . După care puteți extinde parantezele și adăugați termeni similari. Obținem că x 2 + 1 - 5 - x x + x - 2 = x 2 + 1 - 5 + x x + x - 2 = x 2 + x - 4 x + x - 2
- Deoarece numitorii sunt aceiași, nu rămâne decât să adunăm numărătorii, lăsând numitorul: l g 2 x + 4 x (l g x + 2) + 4 l g x x (l g x + 2) = l g 2 x + 4 + 4 x (l g x + 2) + 2)
Adăugarea a fost finalizată. Se poate observa că este posibilă reducerea fracției. Numătorul său poate fi pliat folosind formula pentru pătratul sumei, apoi obținem (l g x + 2) 2 din formule de înmulțire prescurtate. Atunci obținem asta
l g 2 x + 4 + 2 l g x x (l g x + 2) = (l g x + 2) 2 x (l g x + 2) = l g x + 2 x - Date fracții de forma x - 1 x - 1 + x x + 1 cu diferiți numitori. După transformare, puteți trece la adăugare.
Să luăm în considerare o soluție dublă.
Prima metodă este ca numitorul primei fracții să fie factorizat folosind pătrate, cu reducerea sa ulterioară. Obținem o fracțiune din formă
x - 1 x - 1 = x - 1 (x - 1) x + 1 = 1 x + 1
Deci x - 1 x - 1 + x x + 1 = 1 x + 1 + x x + 1 = 1 + x x + 1 .
În acest caz, este necesar să scapi de iraționalitatea în numitor.
1 + x x + 1 = 1 + x x - 1 x + 1 x - 1 = x - 1 + x x - x x - 1
A doua metodă este de a înmulți numărătorul și numitorul celei de-a doua fracții cu expresia x - 1. Astfel, scăpăm de iraționalitate și trecem la adunarea fracțiilor cu același numitor. Apoi
x - 1 x - 1 + x x + 1 = x - 1 x - 1 + x x - 1 x + 1 x - 1 = = x - 1 x - 1 + x x - x x - 1 = x - 1 + x · x - x x - 1
Răspuns: 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + x - 4 x + x - 2, 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) = l g x + 2 x, 3) x - 1 x - 1 + x x + 1 = x - 1 + x · x - x x - 1 .
În ultimul exemplu am constatat că reducerea la un numitor comun este inevitabilă. Pentru a face acest lucru, trebuie să simplificați fracțiile. Când adăugați sau scădeți, trebuie întotdeauna să căutați un numitor comun, care arată ca produsul numitorilor cu factori suplimentari adăugați la numărători.
Exemplul 7
Calculați valorile fracțiilor: 1) x 3 + 1 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) (2 x - 4) - sin x x 5 ln (x + 1) (2 x - 4), 3) 1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x
Soluţie
- Nici unul calcule complexe numitorul nu este necesar, așa că trebuie să alegeți produsul lor de forma 3 x 7 + 2 · 2, apoi alegeți x 7 + 2 · 2 pentru prima fracție ca factor suplimentar și 3 pentru a doua. Când înmulțim, obținem o fracție de forma x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 3 x 7 + 2 2 + 3 1 3 x 7 + 2 2 = = x x 7 + 2 2 + 3 3 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2
- Se poate observa că numitorii sunt prezentați sub forma unui produs, ceea ce înseamnă că transformările suplimentare sunt inutile. Numitorul comun va fi considerat un produs de forma x 5 · ln 2 x + 1 · 2 x - 4 . Prin urmare, x 4
este un factor suplimentar la prima fracție și ln(x + 1)
la al doilea. Apoi scadem si obtinem:
x + 1 x · ln 2 (x + 1) · 2 x - 4 - sin x x 5 · ln (x + 1) · 2 x - 4 = = x + 1 · x 4 x 5 · ln 2 (x + 1) ) · 2 x - 4 - sin x · ln x + 1 x 5 · ln 2 (x + 1) · (2 x - 4) = = x + 1 · x 4 - sin x · ln (x + 1) ) x 5 · ln 2 (x + 1) · (2 x - 4) = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2 x - 4) - Acest exemplu are sens atunci când lucrați cu numitori de fracții. Este necesar să se aplice formulele pentru diferența de pătrate și pătratul sumei, deoarece acestea vor face posibilă trecerea la o expresie de forma 1 cos x - x · cos x + x + 1 (cos x + x) 2. Se poate observa că fracțiile sunt reduse la un numitor comun. Obținem că cos x - x · cos x + x 2 .
Atunci obținem asta
1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x = = 1 cos x - x cos x + x + 1 cos x + x 2 = = cos x + x cos x - x cos x + x 2 + cos x - x cos x - x cos x + x 2 = = cos x + x + cos x - x cos x - x cos x + x 2 = 2 cos x cos x - x cos x + x 2
Răspuns:
1) x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) 2 x - 4 - sin x x 5 · ln (x + 1) · 2 x - 4 = = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2 x - 4) , 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x = 2 · cos x cos x - x · cos x + x 2 .
Exemple de înmulțire a fracțiilor cu variabile
La înmulțirea fracțiilor, numărătorul este înmulțit cu numărătorul și numitorul cu numitorul. Apoi puteți aplica proprietatea de reducere.
Exemplul 8
Înmulțiți fracțiile x + 2 · x x 2 · ln x 2 · ln x + 1 și 3 · x 2 1 3 · x + 1 - 2 sin 2 · x - x.
Soluţie
Înmulțirea trebuie făcută. Înțelegem asta
x + 2 x x 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x) = = x - 2 x 3 x 2 1 3 x + 1 - 2 x 2 ln x 2 ln x + 1 sin (2 x - x)
Numărul 3 este mutat pe primul loc pentru confortul calculelor și puteți reduce fracția cu x 2, apoi obținem o expresie de forma
3 x - 2 x x 1 3 x + 1 - 2 ln x 2 ln x + 1 sin (2 x - x)
Răspuns: x + 2 x x 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x) = 3 x - 2 x x 1 3 x + 1 - 2 ln x 2 · ln x + 1 · sin (2 · x - x) .
Divizia
Împărțirea fracțiilor este similară cu înmulțirea, deoarece prima fracție este înmulțită cu a doua reciprocă. Dacă luăm de exemplu fracția x + 2 x x 2 ln x 2 ln x + 1 și împărțim la 3 x 2 1 3 x + 1 - 2 sin 2 x - x, atunci ea poate fi scrisă ca
x + 2 · x x 2 · ln x 2 · ln x + 1: 3 · x 2 1 3 · x + 1 - 2 sin (2 · x - x) , apoi înlocuiți cu un produs de forma x + 2 · x x 2 · ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x)
Exponentiație
Să trecem la luarea în considerare a operațiilor cu fracții generale cu exponențiere. Dacă există o putere cu exponent natural, atunci acțiunea este considerată ca înmulțire a fracțiilor egale. Dar se recomandă utilizarea unei abordări generale bazate pe proprietățile gradelor. Orice expresii A și C, unde C nu este identic egal cu zero, și orice r real din ODZ pentru o expresie de forma A C r egalitatea A C r = A r C r este valabilă. Rezultatul este o fracție ridicată la o putere. De exemplu, luați în considerare:
x 0, 7 - π · ln 3 x - 2 - 5 x + 1 2, 5 = = x 0, 7 - π · ln 3 x - 2 - 5 2, 5 x + 1 2, 5
Procedura de efectuare a operatiilor cu fractii
Operațiile pe fracții se efectuează după anumite reguli. În practică, observăm că o expresie poate conține mai multe fracții sau expresii fracționale. Apoi, este necesar să efectuați toate acțiunile în ordine strictă: ridicați la o putere, înmulțiți, împărțiți, apoi adăugați și scădeți. Dacă există paranteze, în ele se execută prima acțiune.
Exemplul 9
Calculați 1 - x cos x - 1 c o s x · 1 + 1 x .
Soluţie
Deoarece avem același numitor, atunci 1 - x cos x și 1 c o s x, dar nu se pot face scăderi conform regulii; mai întâi se execută acțiunile din paranteze, apoi înmulțirea și apoi adunarea. Atunci când calculăm, obținem asta
1 + 1 x = 1 1 + 1 x = x x + 1 x = x + 1 x
Când înlocuim expresia în cea originală, obținem că 1 - x cos x - 1 cos x · x + 1 x. La înmulțirea fracțiilor avem: 1 cos x · x + 1 x = x + 1 cos x · x. După ce au făcut toate înlocuirile, obținem 1 - x cos x - x + 1 cos x · x. Acum trebuie să lucrați cu fracții care au numitori diferiți. Primim:
x · 1 - x cos x · x - x + 1 cos x · x = x · 1 - x - 1 + x cos x · x = = x - x - x - 1 cos x · x = - x + 1 cos x x
Răspuns: 1 - x cos x - 1 c o s x · 1 + 1 x = - x + 1 cos x · x .
Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter
Conținutul lecțieiAdunarea fracțiilor cu numitori similari
Există două tipuri de adunări de fracții:
- Adunarea fracțiilor cu numitori similari
- Adunarea fracțiilor cu numitori diferiți
Mai întâi, să învățăm adunarea fracțiilor cu numitori similari. Totul este simplu aici. Pentru a adăuga fracții cu aceiași numitori, trebuie să adăugați numărătorii lor și să lăsați numitorul neschimbat. De exemplu, să adăugăm fracțiile și . Adăugați numărătorii și lăsați numitorul neschimbat:

Acest exemplu poate fi ușor de înțeles dacă ne amintim de pizza, care este împărțită în patru părți. Dacă adăugați pizza la pizza, obțineți pizza:

Exemplul 2. Adăugați fracții și .

Răspunsul s-a dovedit a fi o fracție improprie. Când vine sfârșitul sarcinii, se obișnuiește să scapi de fracțiile improprii. Pentru a scăpa de o fracție necorespunzătoare, trebuie să selectați întreaga parte a acesteia. În cazul nostru, întreaga parte este ușor de izolat - doi împărțiți la doi egal cu unul:

Acest exemplu poate fi ușor de înțeles dacă ne amintim despre o pizza care este împărțită în două părți. Dacă adăugați mai multă pizza la pizza, obțineți o pizza întreagă:

Exemplul 3. Adăugați fracții și .
Din nou, adunăm numărătorii și lăsăm numitorul neschimbat:
![]()
Acest exemplu poate fi ușor de înțeles dacă ne amintim de pizza, care este împărțită în trei părți. Dacă adăugați mai multă pizza la pizza, obțineți pizza:

Exemplul 4. Găsiți valoarea unei expresii 
Acest exemplu este rezolvat exact în același mod ca și cele precedente. Număratorii trebuie adăugați și numitorul lăsat neschimbat:
Să încercăm să descriem soluția noastră folosind un desen. Dacă adăugați pizza la o pizza și adăugați mai multe pizza, obțineți 1 pizza întreagă și mai multe pizza.

După cum puteți vedea, nu este nimic complicat în adunarea fracțiilor cu aceiași numitori. Este suficient să înțelegeți următoarele reguli:
- Pentru a adăuga fracții cu același numitor, trebuie să adăugați numărătorii lor și să lăsați numitorul neschimbat;
Adunarea fracțiilor cu numitori diferiți
Acum să învățăm cum să adunăm fracții cu numitori diferiți. Când se adună fracții, numitorii fracțiilor trebuie să fie aceiași. Dar nu sunt întotdeauna la fel.
De exemplu, fracțiile pot fi adăugate deoarece au aceiași numitori.
Dar fracțiile nu pot fi adăugate imediat, deoarece aceste fracții au numitori diferiți. În astfel de cazuri, fracțiile trebuie reduse la același numitor (comun).
Există mai multe moduri de a reduce fracțiile la același numitor. Astăzi ne vom uita doar la una dintre ele, deoarece celelalte metode pot părea complicate pentru un începător.
Esența acestei metode este că mai întâi este căutat LCM-ul numitorilor ambelor fracții. LCM este apoi împărțit la numitorul primei fracții pentru a obține primul factor suplimentar. Ei fac același lucru cu a doua fracție - LCM este împărțit la numitorul celei de-a doua fracții și se obține un al doilea factor suplimentar.
Numătorii și numitorii fracțiilor sunt apoi înmulțiți cu factorii lor suplimentari. Ca urmare a acestor acțiuni, fracțiile care au numitori diferiți se transformă în fracții care au aceiași numitori. Și știm deja cum să adunăm astfel de fracții.
Exemplul 1. Să adăugăm fracțiile și
În primul rând, găsim cel mai mic multiplu comun al numitorilor ambelor fracții. Numitorul primei fracții este numărul 3, iar numitorul celei de-a doua fracții este numărul 2. Cel mai mic multiplu comun al acestor numere este 6
LCM (2 și 3) = 6
Acum să revenim la fracții și . Mai întâi, împărțiți LCM la numitorul primei fracții și obțineți primul factor suplimentar. LCM este numărul 6, iar numitorul primei fracții este numărul 3. Împărțind 6 la 3, obținem 2.
Numărul rezultat 2 este primul multiplicator suplimentar. O notăm până la prima fracție. Pentru a face acest lucru, faceți o linie oblică mică peste fracție și notați factorul suplimentar găsit deasupra ei:
Facem același lucru cu a doua fracție. Împărțim LCM la numitorul celei de-a doua fracții și obținem al doilea factor suplimentar. LCM este numărul 6, iar numitorul celei de-a doua fracții este numărul 2. Împărțind 6 la 2, obținem 3.
Numărul 3 rezultat este al doilea multiplicator suplimentar. O scriem la a doua fracție. Din nou, facem o linie oblică mică peste a doua fracție și notăm factorul suplimentar găsit deasupra ei:
Acum avem totul pregătit pentru adăugare. Rămâne să înmulțiți numărătorii și numitorii fracțiilor cu factorii lor suplimentari:

Privește cu atenție la ce am ajuns. Am ajuns la concluzia că fracțiile care aveau numitori diferiți s-au transformat în fracții care aveau aceiași numitori. Și știm deja cum să adunăm astfel de fracții. Să luăm acest exemplu până la capăt:

Acest lucru completează exemplul. Se dovedește a adăuga.
Să încercăm să descriem soluția noastră folosind un desen. Dacă adăugați pizza la o pizza, obțineți o pizza întreagă și o altă șesime dintr-o pizza:

Reducerea fracțiilor la același numitor (comun) poate fi, de asemenea, descrisă folosind o imagine. Reducând fracțiile și la un numitor comun, am obținut fracțiile și . Aceste două fracții vor fi reprezentate de aceleași bucăți de pizza. Singura diferență va fi că de data aceasta vor fi împărțite în părți egale (reduse la același numitor).

Primul desen reprezintă o fracție (patru piese din șase), iar al doilea desen reprezintă o fracție (trei piese din șase). Adăugând aceste piese obținem (șapte bucăți din șase). Această fracție este improprie, așa că am evidențiat întreaga parte a ei. Drept urmare, am primit (o pizza întreagă și o altă pizza a șasea).
Vă rugăm să rețineți că am descris acest exemplu prea detaliat. ÎN institutii de invatamant Nu este obișnuit să scrieți atât de detaliat. Trebuie să puteți găsi rapid LCM-ul ambilor numitori și factori suplimentari la aceștia, precum și să înmulțiți rapid factorii suplimentari găsiți cu numărătorii și numitorii dvs. Dacă am fi la școală, ar trebui să scriem acest exemplu după cum urmează:

Dar există și partea din spate medalii. Dacă nu luați note detaliate în primele etape ale studiului matematicii, atunci încep să apară întrebări de acest fel. „De unde vine acel număr?”, „De ce fracțiile se transformă brusc în fracții complet diferite? «.
Pentru a facilita adăugarea fracțiilor cu numitori diferiți, puteți folosi următoarele instrucțiuni pas cu pas:
- Aflați LCM al numitorilor fracțiilor;
- Împărțiți LCM la numitorul fiecărei fracții și obțineți un factor suplimentar pentru fiecare fracție;
- Înmulțiți numărătorii și numitorii fracțiilor cu factorii suplimentari ai acestora;
- Adaugă fracții care au aceiași numitori;
- Dacă răspunsul se dovedește a fi o fracție necorespunzătoare, atunci selectați întreaga sa parte;
Exemplul 2. Găsiți valoarea unei expresii  .
.
Să folosim instrucțiunile de mai sus.
Pasul 1. Aflați LCM al numitorilor fracțiilor
Aflați LCM al numitorilor ambelor fracții. Numitorii fracțiilor sunt numerele 2, 3 și 4

Pasul 2. Împărțiți LCM la numitorul fiecărei fracții și obțineți un factor suplimentar pentru fiecare fracție
Împărțiți LCM la numitorul primei fracții. LCM este numărul 12, iar numitorul primei fracții este numărul 2. Împărțim 12 la 2, obținem 6. Primul factor suplimentar este 6. Îl scriem deasupra primei fracții:
Acum împărțim LCM la numitorul celei de-a doua fracții. LCM este numărul 12, iar numitorul celei de-a doua fracții este numărul 3. Împărțim 12 la 3, obținem 4. Obținem al doilea factor suplimentar 4. Îl scriem deasupra celei de-a doua fracții:
Acum împărțim LCM la numitorul celei de-a treia fracții. LCM este numărul 12, iar numitorul celei de-a treia fracții este numărul 4. Împărțim 12 la 4, obținem 3. Obținem al treilea factor suplimentar 3. Îl scriem deasupra celei de-a treia fracții:
Pasul 3. Înmulțiți numărătorii și numitorii fracțiilor cu factorii suplimentari ai acestora
Înmulțim numărătorii și numitorii cu factorii lor suplimentari:
Pasul 4. Adaugă fracții cu aceiași numitori
Am ajuns la concluzia că fracțiile care aveau numitori diferiți s-au transformat în fracții care aveau aceiași numitori (comuni). Tot ce rămâne este să adunăm aceste fracții. Adaugă:

Adăugarea nu se potrivea pe o singură linie, așa că am mutat expresia rămasă pe următoarea linie. Acest lucru este permis la matematică. Când o expresie nu se încadrează pe o linie, ea este mutată pe următoarea linie și este necesar să se pună un semn egal (=) la sfârșitul primei rânduri și la începutul noii linii. Semnul egal de pe a doua linie indică faptul că aceasta este o continuare a expresiei care a fost pe prima linie.
Pasul 5. Dacă răspunsul se dovedește a fi o fracție necorespunzătoare, atunci selectați întreaga parte a acestuia
Răspunsul nostru s-a dovedit a fi o fracție improprie. Trebuie să evidențiem o întreagă parte din ea. Subliniem:

Am primit un răspuns
Scăderea fracțiilor cu numitori similari
Există două tipuri de scădere de fracții:
- Scăderea fracțiilor cu numitori similari
- Scăderea fracțiilor cu numitori diferiți
În primul rând, să învățăm cum să scădem fracții cu numitori similari. Totul este simplu aici. Pentru a scădea altul dintr-o fracție, trebuie să scădeți numărătorul celei de-a doua fracții de la numărătorul primei fracții, dar numitorul rămâne același.
De exemplu, să găsim valoarea expresiei . Pentru a rezolva acest exemplu, trebuie să scădeți numărătorul celei de-a doua fracții din numărătorul primei fracții și să lăsați numitorul neschimbat. Să o facem:

Acest exemplu poate fi ușor de înțeles dacă ne amintim de pizza, care este împărțită în patru părți. Dacă tăiați pizza dintr-o pizza, obțineți pizza:

Exemplul 2. Găsiți valoarea expresiei.
Din nou, de la numărătorul primei fracții, scădeți numărătorul celei de-a doua fracții și lăsați numitorul neschimbat:

Acest exemplu poate fi ușor de înțeles dacă ne amintim de pizza, care este împărțită în trei părți. Dacă tăiați pizza dintr-o pizza, obțineți pizza:

Exemplul 3. Găsiți valoarea unei expresii 
Acest exemplu este rezolvat exact în același mod ca și cele precedente. Din numărătorul primei fracții trebuie să scădeți numărătorii fracțiilor rămase:

După cum puteți vedea, nu este nimic complicat în scăderea fracțiilor cu aceiași numitori. Este suficient să înțelegeți următoarele reguli:
- Pentru a scădea altul dintr-o fracție, trebuie să scădeți numărătorul celei de-a doua fracții din numărătorul primei fracții și să lăsați numitorul neschimbat;
- Dacă răspunsul se dovedește a fi o fracție necorespunzătoare, atunci trebuie să evidențiați întreaga parte a acestuia.
Scăderea fracțiilor cu numitori diferiți
De exemplu, puteți scădea o fracție dintr-o fracție deoarece fracțiile au aceiași numitori. Dar nu puteți scădea o fracție dintr-o fracție, deoarece aceste fracții au numitori diferiți. În astfel de cazuri, fracțiile trebuie reduse la același numitor (comun).
Numitorul comun se găsește folosind același principiu pe care l-am folosit atunci când adunăm fracții cu numitori diferiți. În primul rând, găsiți LCM al numitorilor ambelor fracții. Apoi LCM se împarte la numitorul primei fracții și se obține primul factor suplimentar, care se scrie deasupra primei fracții. În mod similar, LCM este împărțit la numitorul celei de-a doua fracții și se obține un al doilea factor suplimentar, care este scris deasupra celei de-a doua fracții.
Fracțiile sunt apoi înmulțite cu factorii lor suplimentari. În urma acestor operații, fracțiile care au numitori diferiți sunt convertite în fracții care au aceiași numitori. Și știm deja cum să scădem astfel de fracții.
Exemplul 1. Găsiți sensul expresiei:
Aceste fracții au numitori diferiți, așa că trebuie să le reduceți la același numitor (comun).
Mai întâi găsim LCM al numitorilor ambelor fracții. Numitorul primei fracții este numărul 3, iar numitorul celei de-a doua fracții este numărul 4. Cel mai mic multiplu comun al acestor numere este 12
LCM (3 și 4) = 12
Acum să revenim la fracții și
Să găsim un factor suplimentar pentru prima fracție. Pentru a face acest lucru, împărțiți LCM la numitorul primei fracții. LCM este numărul 12, iar numitorul primei fracții este numărul 3. Împărțiți 12 la 3, obținem 4. Scrieți un patru deasupra primei fracții:
Facem același lucru cu a doua fracție. Împărțiți LCM la numitorul celei de-a doua fracții. LCM este numărul 12, iar numitorul celei de-a doua fracții este numărul 4. Împărțiți 12 la 4, obținem 3. Scrieți un trei peste a doua fracție:
Acum suntem pregătiți pentru scădere. Rămâne să înmulțim fracțiile cu factorii lor suplimentari:

Am ajuns la concluzia că fracțiile care aveau numitori diferiți s-au transformat în fracții care aveau aceiași numitori. Și știm deja cum să scădem astfel de fracții. Să luăm acest exemplu până la capăt:

Am primit un răspuns
Să încercăm să descriem soluția noastră folosind un desen. Dacă tăiați pizza dintr-o pizza, obțineți pizza

Aceasta este versiunea detaliată a soluției. Dacă am fi la școală, ar trebui să rezolvăm mai scurt acest exemplu. O astfel de soluție ar arăta astfel:

Reducerea fracțiilor la un numitor comun poate fi reprezentată și folosind o imagine. Reducând aceste fracții la un numitor comun, am obținut fracțiile și . Aceste fracții vor fi reprezentate de aceleași felii de pizza, dar de data aceasta vor fi împărțite în părți egale (reduse la același numitor):

Prima imagine arată o fracție (opt bucăți din douăsprezece), iar a doua imagine arată o fracție (trei bucăți din douăsprezece). Tăiind trei bucăți din opt bucăți, obținem cinci bucăți din douăsprezece. Fracția descrie aceste cinci piese.
Exemplul 2. Găsiți valoarea unei expresii 
Aceste fracții au numitori diferiți, așa că mai întâi trebuie să le reduceți la același numitor (comun).
Să găsim LCM al numitorilor acestor fracții.
Numitorii fracțiilor sunt numerele 10, 3 și 5. Cel mai mic multiplu comun al acestor numere este 30
LCM(10, 3, 5) = 30
Acum găsim factori suplimentari pentru fiecare fracție. Pentru a face acest lucru, împărțiți LCM la numitorul fiecărei fracții.
Să găsim un factor suplimentar pentru prima fracție. LCM este numărul 30, iar numitorul primei fracții este numărul 10. Împărțim 30 la 10, obținem primul factor suplimentar 3. Îl scriem deasupra primei fracții:
Acum găsim un factor suplimentar pentru a doua fracție. Împărțiți LCM la numitorul celei de-a doua fracții. LCM este numărul 30, iar numitorul celei de-a doua fracții este numărul 3. Împărțim 30 la 3, obținem al doilea factor suplimentar 10. Îl scriem deasupra celei de-a doua fracții:
Acum găsim un factor suplimentar pentru a treia fracție. Împărțiți LCM la numitorul celei de-a treia fracții. LCM este numărul 30, iar numitorul celei de-a treia fracții este numărul 5. Împărțim 30 la 5, obținem al treilea factor suplimentar 6. Îl scriem deasupra celei de-a treia fracții:
Acum totul este gata pentru scădere. Rămâne să înmulțim fracțiile cu factorii lor suplimentari:
Am ajuns la concluzia că fracțiile care aveau numitori diferiți s-au transformat în fracții care aveau aceiași numitori (comuni). Și știm deja cum să scădem astfel de fracții. Să terminăm acest exemplu.
Continuarea exemplului nu se va potrivi pe o linie, așa că mutam continuarea pe următoarea linie. Nu uitați de semnul egal (=) pe noua linie:

Răspunsul s-a dovedit a fi o fracțiune obișnuită și totul pare să ni se potrivească, dar este prea greoi și urât. Ar trebui să o simplificăm. Ce se poate face? Puteți scurta această fracție.
Pentru a reduce o fracție, trebuie să împărțiți numărătorul și numitorul acesteia la (GCD) numerelor 20 și 30.
Deci, găsim mcd-ul numerelor 20 și 30:

Acum revenim la exemplul nostru și împărțim numărătorul și numitorul fracției la mcd găsit, adică la 10

Am primit un răspuns
Înmulțirea unei fracții cu un număr
Pentru a înmulți o fracție cu un număr, trebuie să înmulțiți numărătorul fracției cu acel număr și să lăsați numitorul neschimbat.
Exemplul 1. Înmulțiți o fracție cu numărul 1.
Înmulțiți numărătorul fracției cu numărul 1
![]()
Înregistrarea poate fi înțeleasă ca durând o jumătate de dată. De exemplu, dacă iei pizza o dată, primești pizza

Din legile înmulțirii știm că dacă multiplicandul și factorul sunt schimbate, produsul nu se va schimba. Dacă expresia este scrisă ca , atunci produsul va fi tot egal cu . Din nou, regula pentru înmulțirea unui număr întreg și a unei fracții funcționează:
![]()
Această notație poate fi înțeleasă ca luând jumătate din unu. De exemplu, dacă există 1 pizza întreagă și luăm jumătate din ea, atunci vom avea pizza:

Exemplul 2. Găsiți valoarea unei expresii
Înmulțiți numărătorul fracției cu 4
![]()
Răspunsul a fost o fracție improprie. Să evidențiem întreaga parte a acesteia:
![]()
Expresia poate fi înțeleasă ca luând două sferturi de 4 ori. De exemplu, dacă iei 4 pizza, vei primi două pizza întregi

Și dacă schimbăm multiplicandul și multiplicatorul, obținem expresia . De asemenea, va fi egal cu 2. Această expresie poate fi înțeleasă ca luând două pizza din patru pizza întregi:

Numărul înmulțit cu fracția și numitorul fracției se rezolvă dacă au un factor comun mai mare decât unu.
De exemplu, o expresie poate fi evaluată în două moduri.
Prima cale. Înmulțiți numărul 4 cu numărătorul fracției și lăsați numitorul fracției neschimbat:
![]()
A doua cale. Cele patru fiind înmulțite și cele patru din numitorul fracției pot fi reduse. Acești patru pot fi reduse cu 4, deoarece cel mai mare divizor comun pentru doi patru este patru însuși:

Am obținut același rezultat 3. După reducerea celor patru, în locul lor se formează numere noi: două. Dar înmulțirea unuia cu trei și apoi împărțirea la unu nu schimbă nimic. Prin urmare, soluția poate fi scrisă pe scurt:
Reducerea poate fi efectuată chiar și atunci când am decis să folosim prima metodă, dar la etapa înmulțirii numărului 4 și numărătorului 3 am decis să folosim reducerea:

Dar, de exemplu, expresia poate fi calculată numai în primul mod - înmulțiți 7 cu numitorul fracției și lăsați numitorul neschimbat:
![]()
Acest lucru se datorează faptului că numărul 7 și numitorul fracției nu au un divizor comun mai mare de unu și, în consecință, nu se anulează.
Unii elevi scurtează din greșeală numărul înmulțit și numărătorul fracției. Nu poți face asta. De exemplu, următoarea intrare nu este corectă:
Reducerea unei fracții înseamnă că atât numărătorul cât și numitorul va fi împărțit la același număr. În situația cu expresia, împărțirea se efectuează numai la numărător, deoarece scrierea aceasta este la fel cu scrierea . Vedem că împărțirea se efectuează numai la numărător și nu are loc nicio împărțire la numitor.
Înmulțirea fracțiilor
Pentru a înmulți fracțiile, trebuie să le înmulțiți numărătorii și numitorii. Dacă răspunsul se dovedește a fi o fracție necorespunzătoare, trebuie să evidențiați întreaga parte a acestuia.
Exemplul 1. Găsiți valoarea expresiei.
![]()
Am primit un răspuns. Este recomandabil să reduceți această fracție. Fracția poate fi redusă cu 2. Apoi soluția finală va lua următoarea formă:

Expresia poate fi înțeleasă ca luând o pizza dintr-o jumătate de pizza. Să presupunem că avem jumătate de pizza:
Cum să iau două treimi din această jumătate? Mai întâi trebuie să împărțiți această jumătate în trei părți egale:

Și ia două din aceste trei bucăți:

Vom face pizza. Amintiți-vă cum arată pizza când este împărțită în trei părți:

O bucată din această pizza și cele două bucăți pe care le-am luat vor avea aceleași dimensiuni:

Cu alte cuvinte, vorbim de pizza de aceeași dimensiune. Prin urmare, valoarea expresiei este

Exemplul 2. Găsiți valoarea unei expresii
Înmulțiți numărătorul primei fracții cu numărătorul celei de-a doua fracții și numitorul primei fracții cu numitorul celei de-a doua fracții:

Răspunsul a fost o fracție improprie. Să evidențiem întreaga parte a acesteia:
![]()
Exemplul 3. Găsiți valoarea unei expresii
Înmulțiți numărătorul primei fracții cu numărătorul celei de-a doua fracții și numitorul primei fracții cu numitorul celei de-a doua fracții:
![]()
Răspunsul s-a dovedit a fi o fracție obișnuită, dar ar fi bine dacă ar fi scurtat. Pentru a reduce această fracție, trebuie să împărțiți numărătorul și numitorul acestei fracții la cel mai mare divizor comun (MCD) al numerelor 105 și 450.
Deci, să găsim mcd-ul numerelor 105 și 450:

Acum împărțim numărătorul și numitorul răspunsului nostru la mcd-ul pe care l-am găsit acum, adică la 15
Reprezentarea unui număr întreg sub formă de fracție
Orice număr întreg poate fi reprezentat ca o fracție. De exemplu, numărul 5 poate fi reprezentat ca . Acest lucru nu va schimba sensul lui cinci, deoarece expresia înseamnă „numărul cinci împărțit la unu”, iar acesta, după cum știm, este egal cu cinci:
Numerele reciproce
Acum ne vom familiariza cu un subiect foarte interesant în matematică. Se numește „numere inverse”.
Definiție. Inversa la numărA este un număr care, atunci când este înmulțit cuA dă unul.
Să înlocuim în această definiție în locul variabilei A numărul 5 și încercați să citiți definiția:
Inversa la număr 5 este un număr care, atunci când este înmulțit cu 5 dă unul.
Este posibil să găsim un număr care, înmulțit cu 5, dă unul? Se dovedește că este posibil. Să ne imaginăm cinci ca o fracție:
Apoi înmulțiți această fracție cu ea însăși, schimbați doar numărătorul și numitorul. Cu alte cuvinte, să înmulțim fracția cu ea însăși, doar cu capul în jos:
Ce se va întâmpla ca urmare a acestui fapt? Dacă continuăm să rezolvăm acest exemplu, obținem unul:
![]()
Aceasta înseamnă că inversul numărului 5 este numărul , deoarece atunci când înmulțiți 5 cu obțineți unul.
Reciproca unui număr poate fi găsită și pentru orice alt întreg.
Puteți găsi, de asemenea, reciproca oricărei alte fracții. Pentru a face acest lucru, doar întoarceți-l.
Împărțirea unei fracții la un număr
Să presupunem că avem jumătate de pizza:
Să o împărțim în mod egal între doi. Câtă pizza va primi fiecare persoană?

Se poate observa că după împărțirea jumătății de pizza s-au obținut două bucăți egale, fiecare dintre acestea constituind o pizza. Deci toată lumea primește o pizza.
1. Regula de adunare a fracțiilor cu aceiași numitori:
Exemplul 1:
Exemplul 2:
Regula de adunare a fracțiilor cu numitori diferiți:
Exemplul 1:
Exemplul 2:
Aici numitorii nu au fost înmulțiți, ci a fost luat cel mai mic factor comun a2.
(Numitorul are cea mai mare putere de 2.)
Un factor suplimentar pentru prima fracție este 1, pentru a doua este a.
2. Regula pentru scăderea fracțiilor cu numitori similari:
Regula pentru scăderea fracțiilor cu numitori diferiți:
3. Regula pentru înmulțirea fracțiilor ordinare:
4. Regula pentru împărțirea fracțiilor:
Exemplu:
Fracție obișnuită (simple). Numătorul și numitorul unei fracții.
Fracții proprii și improprii. Număr mixt.
coeficient incomplet. Părți întregi și fracționale. Fracții inverse. O parte dintr-o unitate sau mai multe părți ale acesteia se numesc fracție obișnuită sau simplă. Cantitate părti egale, în care se împarte unitatea se numește numitor, iar numărul de părți luate se numește numărător. Fracția se scrie astfel:
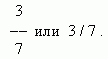
Aici 3 este numărătorul, 7 este numitorul.
Dacă numărătorul este mai mic decât numitorul, atunci fracția este mai mică decât 1 și se numește Fracțiunea corespunzătoare. Dacă numărătorul este egal cu numitorul, atunci fracția este egală cu 1. Dacă numărătorul este mai mare decât numitorul, atunci fracția este mai mare decât 1. În ambele cazuri din urmă, fracția se numește improprie. Dacă numărătorul este împărțit la numitor, atunci această fracție este egală cu câtul împărțirii: 63 / 7 = 9. Dacă împărțirea se face cu rest, atunci această fracție improprie poate fi reprezentată număr mixt:
Aici 9 - coeficient incomplet(partea întreagă a unui număr mixt), 2 – rest (numărătorul părții fracționale), 7 – numitorul.
Este adesea necesar să se rezolve problema inversă - inversează un număr mixt intr-o fractiune. Pentru a face acest lucru, înmulțiți partea întreagă a numărului mixt cu numitorul și adăugați numărătorul părții fracționale. Acesta va fi numărătorul fracției comune, dar numitorul rămâne același. 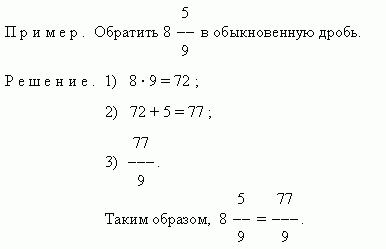
Fracțiile reciproce sunt două fracții al căror produs este egal cu 1. De exemplu, 3 / 7 și 7 / 3; 15/1 și 1/15 etc.
Expansiunea fracțiilor. Reducerea unei fracții. Compararea fracțiilor.
Reducere la un numitor comun. Adunare si scadere fractii.
Înmulțirea fracțiilor. Împărțirea fracțiilor
Expansiunea fracțiilor.Valoarea unei fracții nu se modifică dacă numărătorul și numitorul ei sunt înmulțiți cu același număr, altul decât zero, prin extinderea fracției. De exemplu,
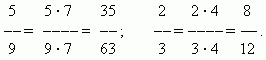
Reducerea unei fracții. Valoarea unei fracții nu se schimbă dacă împărțiți numărătorul și numitorul acesteia la același număr, altul decât zero.. Această transformare se numeștereducerea unei fracții. De exemplu, 
Compararea fracțiilor.Dintre două fracții cu aceiași numărători, cea al cărei numitor este mai mic este mai mare:

Dintre două fracții cu același numitor, cea al cărei numărător este mai mare este mai mare:

Pentru a compara fracții care au numărători și numitori diferiți, trebuie să le extindeți pentru a le aduce la un numitor comun.
EXEMPLU Comparați două fracții:
Transformarea folosită aici se numește reducerea fracțiilor la un numitor comun.
Adunarea și scăderea fracțiilor.Dacă numitorii fracțiilor sunt aceiași, atunci pentru a adăuga fracțiile, trebuie să adăugați numărătorii lor, iar pentru a scădea fracțiile, trebuie să scădeți numărătorii lor (în aceeași ordine). Suma sau diferența rezultată va fi numărătorul rezultatului; numitorul va rămâne același. Dacă numitorii fracțiilor sunt diferiți, mai întâi trebuie să reduceți fracțiile la un numitor comun. Când se adaugă numere mixte, părțile lor întregi și fracționale sunt adăugate separat. Când scădeți numere mixte, vă recomandăm mai întâi să le convertiți în fracții improprii, apoi să scădeți una din cealaltă și apoi să convertiți din nou rezultatul, dacă este necesar, în formă de numere mixte.
EXEMPLU
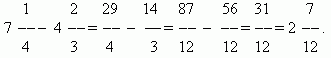
Înmulțirea fracțiilor.A înmulți un număr cu o fracție înseamnă a-l înmulți cu numărător și a împărți produsul la numitor. Prin urmare, avem o regulă generală pentru înmulțirea fracțiilor:pentru a înmulți fracții, trebuie să le înmulțiți separat numărătorii și numitorii și să împărțiți primul produs la al doilea.
EXEMPLU 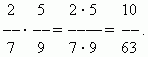
Împărțirea fracțiilor. Pentru a împărți un anumit număr la o fracție, este necesar să se înmulțească acest număr cu fracția reciprocă.Această regulă rezultă din definiția împărțirii (vezi secțiunea „Operații aritmetice”).
EXEMPLU 
Zecimal. Toată parte. Punct zecimal.
Zecimale. Proprietățile fracțiilor zecimale.
Fracție zecimală periodică. Perioadă
Zecimaleste rezultatul împărțirii unu la zece, o sută, mie etc. părți. Aceste fracții sunt foarte convenabile pentru calcule, deoarece se bazează pe același sistem pozițional pe care se bazează numărarea și scrierea numerelor întregi. Datorită acestui fapt, notația și regulile de lucru cu fracții zecimale sunt în esență aceleași ca pentru numerele întregi. Când scrieți fracții zecimale, nu este nevoie să marcați numitorul; acesta este determinat de locul ocupat de cifra corespunzătoare. Mai întâi este scrisîntreaga parte numere, apoi puneți în dreaptapunct zecimal. Prima cifră după virgulă înseamnă numărul de zecimi, a doua - numărul de sutimi, a treia - numărul de miimi etc. Sunt numite numerele situate după virgulăzecimale.
EXEMPLU 
Unul dintre avantajele fracțiilor zecimale este că se reduc cu ușurință la fracții obișnuite: numărul de după virgulă (în cazul nostru 5047) este numărătorul; numitorul este egal n -a putere de 10, unde n - numărul de zecimale (în cazul nostru n = 4): 
Dacă fracția zecimală nu conține o parte întreagă, atunci un zero este plasat înaintea virgulei zecimale:
Proprietățile fracțiilor zecimale.
1. Decimala nu se schimbă dacă adăugați zerouri la dreapta:
2.
Fracția zecimală nu se schimbă dacă eliminați zerourile aflate
la sfârşitul zecimalei:
0.00123000 = 0.00123 .
Atenție! Nu puteți elimina zerouri care nu sunt situate la sfârșit zecimal!br />
Aceste proprietăți vă permit să înmulțiți și să împărțiți rapid zecimale cu 10, 100, 1000 etc.
zecimală periodică conține un grup de numere care se repetă la infinit numită perioadă. Perioada este scrisă între paranteze. De exemplu, 0,12345123451234512345... = 0.(12345).
EXEMPLU Dacă împărțim 47 la 11, obținem 4,27272727... = 4.(27).
Înmulțirea zecimalelor.
Împărțirea zecimale.
Adunarea și scăderea zecimalelor. Aceste operații sunt efectuate în același mod ca și adunarea și scăderea numerelor întregi. Trebuie doar să notați zecimalele corespunzătoare una sub alta.
EXEMPLU
Înmulțirea zecimalelor.În prima etapă, înmulțim fracțiile zecimale ca numere întregi, fără a ține cont de punctul zecimal. Atunci se aplică următoarea regulă: numărul de zecimale din produs este egal cu suma zecimale din toți factorii.
Notă: înainte de a introduce punctul zecimal înprodusul nu poate fi aruncat cu zerouri finale!
EXEMPLU
Suma numerelor zecimale din factori este egală cu: 3 + 4 = 7. Suma numerelor din produs este 6. Prin urmare, trebuie să adăugați un zero la stânga: 0197056 și să puneți un punct zecimal în fața acestuia: 0,0197056.
Împărțire zecimală
Împărțirea unei zecimale la un număr întreg
Dacă dividendul este mai mic decât divizorul, scrieți un zero în partea întreagă a coeficientului și puneți un punct zecimal după el. Apoi, fără a lua în considerare punctul zecimal al dividendului, adăugăm următoarea cifră a părții fracționale la partea sa întreagă și comparăm din nou partea întreagă rezultată a dividendului cu divizorul. Dacă noul număr este din nou mai mic decât divizorul, punem un alt zero după punctul zecimal din coeficient și adăugăm următoarea cifră a părții sale fracționale la întreaga parte a dividendului. Repetăm acest proces până când dividendul rezultat devine mai mare decât divizorul. După aceasta, împărțirea este efectuată ca pentru numere întregi. Dacă dividendul este mai mare sau egal cu divizorul, mai întâi împărțim întreaga sa parte, scriem rezultatul împărțirii în cât și punem virgulă. După aceasta, împărțirea continuă ca și în cazul numerelor întregi.
EXEMPLU Împărțiți 1,328 la 64.
Soluţie: 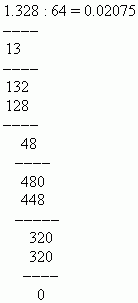
Împărțirea unei fracții zecimale la alta.
În primul rând, transferăm punctele zecimale din dividend și divizor la numărul de zecimale din divizor, adică facem divizorul un număr întreg. Acum efectuăm împărțirea ca în cazul precedent.
EXEMPLU Împărțiți 0,04569 la 0,0006.
Rezolvare: Mutați zecimale cu 4 poziții la dreapta și împărțiți 456,9 la 6:

Pentru a converti o fracție zecimală într-o fracție obișnuită, trebuie să luați numărul de după virgulă ca numărător și să luați a n-a putere a lui zece ca numitor (aici n este numărul de zecimale). Partea întreagă diferită de zero este stocată într-o fracție obișnuită; partea întreagă zero este omisă. De exemplu: 
Pentru a converti o fracție într-o zecimală, trebuie să împărțiți numărătorul la numitor în conformitate cu regulile de împărțire.
EXEMPLU Convertiți 5/8 într-o zecimală.
Rezolvare: Împărțind 5 la 8 dă 0,625. (Nota, vă rog!).
În cele mai multe cazuri, acest proces poate continua pe termen nelimitat. Atunci este imposibil să convertiți cu exactitate o fracție într-o zecimală. Dar, în practică, acest lucru nu este niciodată necesar. Împărțirea este întreruptă dacă zecimalele de interes au fost deja obținute.
EXEMPLU Convertiți 1/3 într-o zecimală.
Rezolvare: Împărțirea lui 1 la 3 va fi infinită: 1:3 = 0,3333… .
Verificați-l vă rog!