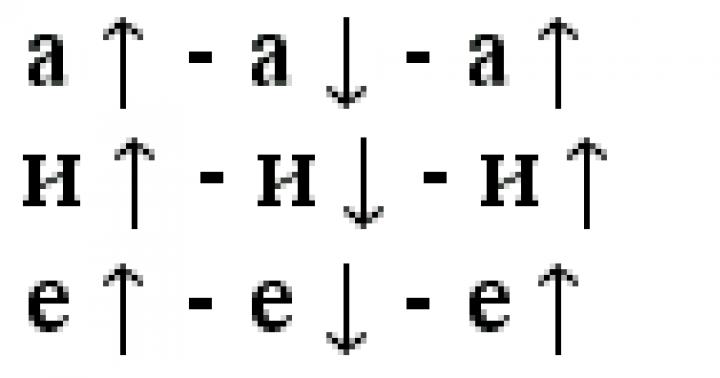![]()
Regula de trei sigma
Înlocuiți o valoare? în formula (*), obținem:
Deci, cu o probabilitate arbitrar apropiată de unu, se poate argumenta că modulul de abatere al unei variabile aleatoare distribuite normal de la așteptarea ei matematică nu depășește de trei ori abaterea standard.
Teorema limitei centrale.
Teorema limită centrală este un grup de teoreme dedicate stabilirii condițiilor în care a legea normală distributie. Dintre aceste teoreme, locul cel mai important îi revine teoremei lui Lyapunov.
Dacă variabila aleatoare X este suma unui număr mare reciproc? variabile aleatoare independente, adică influența fiecăreia asupra întregii sume este neglijabilă, apoi variabila aleatoare X are o distribuție care se apropie la infinit de o distribuție normală.
Momentele inițiale și centrale ale unei variabile aleatoare continue, asimetrie și curtoză. Mod și mediană.
În probleme aplicate, de exemplu, în statistica matematică, în studiul teoretic al distribuțiilor empirice care diferă de distributie normala, devine necesară cuantificarea acestor diferențe. În acest scop, sunt introduse caracteristici speciale adimensionale.
Definiție. Modul unei variabile aleatoare continue (Mo (X)) este valoarea sa cea mai probabilă, pentru care probabilitatea p i sau densitatea de probabilitate f(x) atinge maximul său.
Definiție. Mediana unei variabile aleatoare continue X (Pe mine(X)) este valoarea sa pentru care egalitatea este adevărată:
Geometric, linia verticală x = Me (X) împarte aria figurii de sub curbă în două părți egale.
În punctul X = Me(X), funcția de distribuție F(Me(X)) =
Aflați modul Mo, mediana Me și așteptarea matematică M a unei variabile aleatoare X cu o densitate de probabilitate f(x) = 3x 2 , pentru x I [ 0; unu ].
Densitatea de probabilitate f(x) este maximă la x = 1, adică. f (1) = 3, deci Mo (X) = 1 pe intervalul [ 0; unu ].
Pentru a găsi mediana, notează Me (X) = b.
Deoarece Me (X) satisface condiția P (X 3 = .
b 3 = ; b = » 0,79
M(X) ==+ ![]() =
=
Observați cele 3 valori rezultate Mo (x), Me (X), M (X) pe axa Ox:

Definiție. asimetrie distribuția teoretică este raportul dintre momentul central de ordinul trei și cubul deviației standard:
Definiție. curtoză distribuția teoretică se numește valoarea determinată de egalitate:
Unde ? moment central de ordinul al patrulea.
Pentru o distribuție normală. Când se abate de la o distribuție normală, asimetria este pozitivă dacă partea „lungă” și mai plată a curbei de distribuție este situată la dreapta punctului de pe axa x corespunzător modului; dacă această parte a curbei este situată în stânga modului, atunci asimetria este negativă (Fig. 1, a, b).

Kurtosis caracterizează „abruptul” creșterii curbei de distribuție în comparație cu curba normală: dacă kurtosis este pozitiv, atunci curba are un vârf mai înalt și mai ascuțit; în cazul curtozei negative, curba comparată are un vârf mai mic și mai plat.
Trebuie avut în vedere faptul că atunci când utilizați caracteristici specificate Comparațiile se bazează pe ipotezele despre aceleași valori ale așteptărilor matematice și ale varianței pentru distribuția normală și teoretică.
Exemplu. Fie o variabilă aleatoare discretă X dat de legea distributiei:

Aflați: asimetria și curtoza distribuției teoretice.
Să găsim mai întâi așteptările matematice ale unei variabile aleatorii:
Apoi calculăm momentele inițiale și centrale ale ordinului 2, 3 și 4 și:

Acum, folosind formulele, găsim valorile necesare:

În acest caz, partea „lungă” a curbei de distribuție este situată în dreapta modului, iar curba în sine este oarecum mai aprinsă decât curba normală, cu aceleași valori ale așteptărilor și varianței matematice.
Teorema. Pentru o variabilă aleatoare arbitrară Xși orice număr
?>0 sunt valabile următoarele inegalități:
![]()
![]()
Probabilitatea inegalității opuse.
Consumul mediu de apă la o fermă zootehnică este de 1000 de litri pe zi, iar abaterea standard a acestei variabile aleatorii nu depășește 200 de litri. Estimați probabilitatea ca consumul de apă la fermă într-o zi dată să nu depășească 2000 de litri folosind inegalitatea Chebyshev.
Lăsa X– consumul de apă la ferma zootehnică (l).
Dispersia D(X) = . Deoarece limitele intervalului 0 X 2000 sunt simetrice în raport cu așteptările matematice M(X) = 1000, apoi pentru a estima probabilitatea evenimentului dorit, putem aplica inegalitatea Chebyshev:
Adică nu mai puțin de 0,96.
Pentru distribuția binomială, inegalitatea Chebyshev ia forma:
LEGILE DISTRIBUȚIEI VARIABILLOR ALEATORII
LEGILE DISTRIBUȚIEI VARIABILLOR ALEATORII - secțiunea Matematică, TEORIA PROBABILITĂȚII ȘI STATISTICA MATEMATICĂ Cele mai comune legi sunt uniforme, normale și exponențială.
Legile distribuției uniforme, normale și exponențiale a probabilităților variabilelor aleatoare continue sunt cel mai des întâlnite.
Distribuția de probabilitate a unei variabile aleatoare continue X se numește uniformă dacă în intervalul (a, b) căruia îi aparțin toate valorile posibile ale lui X, densitatea distribuției rămâne constantă (6.1)
Funcția de distribuție are forma:
Normală este distribuția de probabilitate a unei variabile aleatoare continue X, a cărei densitate are forma:
Probabilitatea ca o variabilă aleatoare X să ia o valoare aparținând intervalului (?; ?):
unde este funcția Laplace și,
Care este probabilitatea ca valoarea absolută a abaterii să fie mai mică decât un număr pozitiv?:
În special, pentru a = 0, . (6,7)
Exponențialul (exponențialul) este distribuția de probabilitate a unei variabile aleatoare continue X, care este descrisă de densitatea:
Unde? este o valoare pozitivă constantă.
Funcția de distribuție a legii exponențiale:
Probabilitatea de a lovi o variabilă aleatoare continuă X în intervalul (a, c), distribuită conform legii exponențiale:
1. Valoare aleatoare X este distribuit uniform în intervalul (-2; N). Aflați: a) funcția diferențială a variabilei aleatoare X; b) funcţia integrală; c) probabilitatea ca o variabilă aleatoare să cadă în intervalul (-1;); d) așteptarea matematică, varianța și abaterea standard a unei variabile aleatoare X.
2. Aflați așteptarea și varianța matematică a unei variabile aleatoare distribuite uniform în intervalul: a) (5; 11); b) (-3; 5). Desenați grafice ale acestor funcții.
3. Variabila aleatoare X este distribuită uniform pe intervalul (2; 6), iar D(x) = 12. Aflați funcțiile de distribuție ale variabilei aleatoare X. Desenați grafice ale funcțiilor.
4. Variabila aleatoare X este distribuită conform legii triunghi dreptunghic(Fig. 1) în intervalul (0; a). Aflați: a) funcția diferențială a variabilei aleatoare X; b) funcţia integrală; c) probabil
probabilitatea de a atinge o variabilă aleatoare
la interval(); d) matematică
așteptare, varianță și pătrat mediu
abatere aleatorie
5. Variabila aleatoare X este distribuită conform legii lui Simpson („legea triunghi isoscel”) (Fig. 2) pe intervalul (-a; a). Aflați: a) funcția de distribuție a probabilității diferențiale a variabilei aleatoare X;
b) o funcție integrală și reprezentați graficul acesteia; c) probabilitatea ca o variabilă aleatoare să cadă în intervalul (-); d) așteptarea matematică, varianța și abaterea standard a unei variabile aleatoare X.
6. Pentru a studia productivitatea unei anumite rase de păsări se măsoară diametrul ouălor. Cel mai mare diametru transversal al ouălor este o variabilă aleatorie distribuită conform legii normale cu o valoare medie de 5 cm și o abatere standard de 0,3 cm.Aflați probabilitatea ca: a) diametrul unui ou luat la întâmplare să fie între 4,7 și 6, 2 cm; b) abaterea diametrului de la medie nu depăşeşte 0,6 cm în valoare absolută.
7. Greutatea peștelui prins în iaz respectă legea distribuției normale cu o abatere standard de 150 g și așteptări matematice a \u003d 1000 g. Aflați probabilitatea ca greutatea peștelui prins să fie: a) de la 900 la 1300 g; b) nu mai mult de 1500 g; c) nu mai puțin de 800 g; d) diferă de greutatea medie modulo nu mai mult de 200 g; e) trageți un grafic al funcției diferențiale a variabilei aleatoare X.
8. Randamentul de grâu de toamnă pentru totalitatea parcelelor se repartizează conform legii normale cu următorii parametri: a = 50 c/ha, = 10 c/ha. Determinaţi: a) ce procent de parcele vor avea un randament mai mare de 40 c/ha; b) procentul de parcele cu un randament de 45 până la 60 c/ha.
9. Metoda selectiva se măsoară buruienile cerealelor, erorile de măsurare aleatoare sunt supuse unei legi de distribuție normală cu o abatere standard de 0,2 g și așteptarea matematică a = 0. Aflați probabilitatea ca, din patru măsurători independente, eroarea a cel puțin uneia dintre ele să nu fie depășește 0,3 g în valoare absolută.
10. Cantitatea de cereale recoltată din fiecare parcelă a câmpului experimental este o variabilă aleatoare X distribuită normal, care are așteptarea matematică a = 60 kg și abaterea standard este de 1,5 kg. Aflați intervalul în care cantitatea X va fi închisă cu o probabilitate de 0,9906. Scrieți funcția diferențială a acestei variabile aleatoare.
11. Cu o probabilitate de 0,9973, s-a constatat că abaterea absolută a greutății în viu a unui capete de vite prelevat aleatoriu de la greutatea medie a animalului în întregul efectiv nu depășește 30 kg. Aflați abaterea standard a greutății în viu a animalelor, presupunând că distribuția efectivelor în funcție de greutatea în viu respectă legea normală.
12. Randamentul de legume pe parcele este o variabilă aleatoare distribuită normal, cu o așteptare matematică de 300 c/ha și o abatere standard de 30 c/ha. Cu o probabilitate de 0,9545, determinați limitele în care va fi randamentul mediu de legume din parcele.
13. Variabila aleatoare X distribuită normal este dată de o funcție diferențială:
Determinaţi: a) probabilitatea ca o variabilă aleatoare să cadă în interval
(3; 9); b) modul și mediana variabilei aleatoare X.
14. O societate comercială vinde același tip de produse de la doi producători. Durata de viață a produselor este supusă legii normale. Durata medie de viață a produselor primului producător este de 5,5 mii de ore, iar al doilea - 6 mii de ore. Primul producător susține că, cu o probabilitate de 0,95, durata de viață a primului producător este în intervalul de la 5 la 6 mii de ore, iar al doilea, cu o probabilitate de 0,9, este în intervalul de la 5 la 7 mii de ore. Care producător are cea mai mare variabilitate în viața produsului.
15. Salariile lunare ale angajaților întreprinderii sunt distribuite conform legii normale cu așteptarea matematică a = 10 mii de ruble. Se știe că 50% dintre angajații companiei primesc salarii de la 8 la 12 mii de ruble. Determinați ce procent din angajații companiei au un salariu lunar de 9 până la 18 mii de ruble.
16. Scrieţi funcţia de densitate şi distribuţie a legii exponenţiale dacă: a) un parametru; b) ; în) . Desenați grafice ale funcțiilor.
17. De altfel, variabila aleatoare X este distribuită conform legii exponenţiale. Aflați probabilitatea de a lovi o variabilă aleatoare X în intervalul: a) (0; 1); b) (2; 4). M(X), D(X), (X).
18. Aflați M(X), D(X), (X) ale legii exponențiale de distribuție a unei variabile aleatoare X de o funcție dată:
19. Două elemente de operare independentă sunt testate. Timpul de funcționare al primului are o distribuție mai indicativă decât al doilea. Aflați probabilitatea ca în decurs de 20 de ore: a) ambele elemente să funcționeze; b) un singur element va eșua; c) cel puţin un element defectează; d) ambele elemente vor eșua.
20. Probabilitatea ca ambele elemente independente să funcționeze timp de 10 zile este de 0,64. Determinați funcția de fiabilitate pentru fiecare element dacă funcțiile sunt aceleași.
21. Numărul mediu de erori pe care operatorul le face pe parcursul unei ore de muncă este de 2. Aflați probabilitatea ca în 3 ore de muncă operatorul să comită: a) 4 erori; b) cel puţin două greşeli; c) cel puţin o greşeală.
22. Numărul mediu de apeluri care sosesc la PBX într-un minut este de trei. Aflați probabilitatea ca în 2 minute să fie: a) 4 apeluri; b) cel puţin trei apeluri.
23. Variabila aleatoare X este distribuită conform legii Cauchy
Variabile aleatoare continue
6. Variabile aleatoare continue
6.1. Caracteristicile numerice ale variabilelor aleatoare continue
O variabilă continuă este o variabilă aleatoare care poate lua toate valorile dintr-un interval finit sau infinit.
Funcția de distribuție se numește funcția F (x) ? determinarea probabilității ca variabila aleatoare X ca urmare a testului să ia o valoare mai mică decât x, adică.
Proprietățile funcției de distribuție:
1. Valorile funcției de distribuție aparțin segmentului , i.e.
2. F (x) este o funcție nedescrescătoare, adică. daca atunci .
Probabilitatea ca o variabilă aleatoare X să ia o valoare conținută în interval este egală cu:
· Probabilitatea ca o variabilă aleatoare continuă X să ia o valoare definită este egală cu zero.
Densitatea distribuției de probabilitate a unei variabile aleatoare continue X se numește funcție - prima derivată a funcției de distribuție.
Probabilitatea de a atinge o variabilă aleatoare continuă într-un interval dat:
Găsirea funcției de distribuție dintr-o densitate de distribuție cunoscută:
Proprietăți de densitate de distribuție
1. Densitatea distribuției este o funcție nenegativă:
2. Condiție de normalizare:
Deviație standard
6.2. Distributie uniforma
O distribuție de probabilitate se numește uniformă dacă, în intervalul căruia îi aparțin toate valorile posibile ale variabilei aleatoare, densitatea distribuției rămâne constantă.
Densitatea de probabilitate a unei variabile aleatoare distribuite uniform
Deviație standard
6.3. Distributie normala
Normal este distribuția de probabilitate a unei variabile aleatoare, care este descrisă de densitatea distribuției
a - așteptarea matematică
deviație standard
dispersie
Probabilitatea de a atinge intervalul
Unde este funcția Laplace. Această funcție tabulate, adică integrala nu trebuie calculată, este necesar să folosiți tabelul.
Probabilitatea de abatere a unei variabile aleatoare x de la așteptarea matematică
Regula trei sigma
Dacă o variabilă aleatoare este distribuită în mod normal, atunci valoarea absolută a abaterii ei de la așteptarea matematică nu depășește de trei ori abaterea standard.
Pentru a fi precis, probabilitatea de a depăși intervalul specificat este de 0,27%
Calculator online pentru probabilitatea distribuției normale
6.4. distribuție exponențială
O variabilă aleatoare X este distribuită conform unei legi exponențiale dacă densitatea distribuției are forma
Deviație standard
O caracteristică distinctivă a acestei distribuții este că așteptarea matematică este egală cu abaterea standard.
Teoria probabilității. Evenimente aleatorii (pagina 6)

12. Variabile aleatorii X ![]() , dacă , , , .
, dacă , , , .
13. Probabilitatea de a produce un produs defect este de 0,0002. Calculați probabilitatea ca un inspector care verifică calitatea a 5000 de articole să găsească 4 articole defecte printre ele.
X  X va lua o valoare aparținând intervalului . Trasează funcțiile și .
X va lua o valoare aparținând intervalului . Trasează funcțiile și .
15. Probabilitatea de funcționare fără defecțiuni a elementului este distribuită conform legii exponențiale ![]() (). Găsiți probabilitatea ca elementul să funcționeze impecabil timp de 50 de ore.
(). Găsiți probabilitatea ca elementul să funcționeze impecabil timp de 50 de ore.
16. Dispozitivul este format din 10 elemente de acționare independentă. Probabilitatea de defectare a fiecărui element în timp T este egal cu 0,05. Folosind inegalitatea Chebyshev, estimați probabilitatea ca valoarea absolută a diferenței dintre numărul de elemente eșuate și numărul mediu (așteptarea) de eșecuri în timp T va fi mai puțin de două.
17. Trei focuri independente au fost trase în țintă (în Fig. 4.1 m, m) fără o eroare sistematică () cu răspândirea așteptată a loviturii m. Aflați probabilitatea ca cel puțin o lovire pe țintă.

1. Câte numere din trei cifre pot fi făcute din numerele 0,1,2,3,4,5?
2. Corul este format din 10 membri. În câte moduri pot fi aleși 6 participanți pentru 3 zile, astfel încât în fiecare zi să existe o formație diferită a corului?
3. În câte moduri poate fi împărțit în jumătate un pachet de 52 de cărți amestecate astfel încât să fie trei ași într-o jumătate?
4. Dintr-o cutie care conține jetoane cu numere de la 1 la 40, participanții la extragere trag jetoane. Determinați probabilitatea ca numărul primului jeton extras la întâmplare să nu conțină numărul 2.
5. Pe bancul de testare sunt testate 250 de dispozitive in anumite conditii. Găsiți probabilitatea ca cel puțin unul dintre dispozitivele testate să se defecteze în decurs de o oră, dacă se știe că probabilitatea de defecțiune într-o oră a unuia dintre aceste dispozitive este egală cu 0,04 și este aceeași pentru toate dispozitivele.
6. Există 10 puști în piramidă, dintre care 4 sunt echipate cu o vizor optic. Probabilitatea ca trăgătorul să lovească ținta atunci când este tras de la o pușcă cu o vizor telescopic este de 0,95; pentru puștile fără vizor telescopic, această probabilitate este de 0,8. Trăgătorul a lovit ținta cu o pușcă luată la întâmplare. Găsiți probabilitatea ca trăgătorul să tragă dintr-o pușcă cu o vizor optic.
7. Dispozitivul este format din 10 noduri. Fiabilitate (probabilitatea de funcționare fără defecțiuni în timp t pentru fiecare nod este egal cu . Nodurile eșuează independent unul de celălalt. Găsiți probabilitatea ca în timp t: a) cel puţin un nod va eşua; b) exact două noduri vor eșua; c) exact un nod va eșua; d) cel puțin două noduri vor eșua.
8. Fiecare dintre cele 16 elemente ale unui dispozitiv este testat. Probabilitatea ca un element să treacă testul este de 0,8. Găsiți numărul cel mai probabil de elemente care vor trece testul.
9. Găsiți probabilitatea ca evenimentul DAR(schimbarea vitezelor) va avea loc de 70 de ori pe o pistă de 243 de kilometri dacă probabilitatea de schimbare pe kilometru al acelei linii este de 0,25.
10. Probabilitatea de a lovi ținta cu o singură lovitură este de 0,8. Găsiți probabilitatea ca cu 100 de lovituri ținta să fie lovită de cel puțin 75 de ori și de cel mult 90 de ori.
X.
12. Variabile aleatorii X si independenta. Aflați așteptările matematice și varianța unei variabile aleatoare ![]() , dacă , , , .
, dacă , , , .
13. Manuscrisul de 1000 de pagini de text dactilografiat conține 100 de greșeli de tipărire. Găsiți probabilitatea ca o pagină selectată aleatoriu să conțină exact 2 greșeli de tipărire.
14. Variabilă aleatoare continuă X distribuit uniform cu o densitate de probabilitate constantă, unde  Găsiți 1) parametrul și notați legea distribuției; 2) Găsiți , ; 3) Aflați probabilitatea ca X va lua o valoare aparținând intervalului .
Găsiți 1) parametrul și notați legea distribuției; 2) Găsiți , ; 3) Aflați probabilitatea ca X va lua o valoare aparținând intervalului .
15. Timpul de funcționare al unui element are o distribuție exponențială ![]() (). Găsiți probabilitatea ca t= 24 de ore elementul nu va eșua.
(). Găsiți probabilitatea ca t= 24 de ore elementul nu va eșua.
16. Variabilă aleatoare continuă X distribuite conform legii normale  . Găsi , . Găsiți probabilitatea ca în urma testului X va lua valoarea cuprinsă în intervalul .
. Găsi , . Găsiți probabilitatea ca în urma testului X va lua valoarea cuprinsă în intervalul .
17. Distribuția de probabilitate a unei variabile aleatoare bidimensionale discrete este dată:
Aflați legea distribuției componentelor Xși ; așteptările lor matematice și ; varianțe și ; coeficient de corelație .
1. Câte numere din trei cifre pot fi făcute din numerele 1,2, 3, 4, 5 dacă fiecare dintre aceste numere este folosit nu mai mult de o dată?
2. Dat n puncte, dintre care 3 se află pe aceeași linie. Câte linii pot fi trase conectând punctele în perechi?
Câte piese de domino pot fi făcute folosind numere de la 0 la 9?
3. Care este probabilitatea ca o foaie ruptă aleatoriu din noul calendar să corespundă cu prima zi a lunii? (Anul nu este considerat un an bisect.)
4. In atelier sunt 3 telefoane care functioneaza independent unele de altele.
5. Probabilităţile de angajare ale fiecăruia dintre ei sunt, respectiv, următoarele: ; ; . Găsiți probabilitatea ca cel puțin un telefon să fie liber.
6. Sunt trei urne identice. Prima urnă conține 20 de bile albe, a doua urnă conține 10 bile albe și 10 negre, iar a treia urnă conține 20 de bile negre. Dintr-o urna aleasa la intamplare se extrage o bila alba. Găsiți probabilitatea ca mingea să fie extrasă din prima urnă.
7. În unele zone vara, în medie, 20% din zile sunt ploioase. Care este probabilitatea ca într-o săptămână: a) să fie cel puţin o zi ploioasă; b) va fi exact o zi ploioasă; c) numărul de zile ploioase nu va fi mai mare de patru; d) nu vor fi zile ploioase.
8. Probabilitatea de încălcare a preciziei în asamblarea dispozitivului este de 0,32. Determinați cel mai probabil număr de instrumente de precizie într-un lot de 9 bucăți.
9. Determinați probabilitatea ca la 150 de lovituri de la o pușcă ținta să fie lovită de 70 de ori dacă probabilitatea de a lovi ținta cu o singură lovitură este de 0,4.
10. Determinați probabilitatea ca din 1000 de copii născuți numărul de băieți să fie de cel puțin 455 și de cel mult 555, dacă probabilitatea de naștere a băieților este de 0,515.
11. Este dată legea distribuției unei variabile aleatoare discrete X:
Aflați: 1) valoarea probabilității corespunzătoare valorii ; 2) , , ; 3) funcția de distribuție; construiește-i graficul. Construiți un poligon de distribuție al unei variabile aleatoare X.
12. Variabile aleatorii X si independenta. Aflați așteptările matematice și varianța unei variabile aleatoare ![]() , dacă , , , .
, dacă , , , .
13. Probabilitatea de a produce o piesă nestandard este de 0,004. Găsiți probabilitatea ca între 1000 de părți să fie 5 non-standard.
14. Variabilă aleatoare continuă X dat de funcţia de distribuţie  Găsiți: 1) funcția de densitate ; 2) , , ; 3) probabilitatea ca, în urma experimentului, variabila aleatoare X va lua o valoare aparținând intervalului . Construiți grafice ale funcțiilor și .km, km. Determinați probabilitatea de două lovituri asupra țintei.
Găsiți: 1) funcția de densitate ; 2) , , ; 3) probabilitatea ca, în urma experimentului, variabila aleatoare X va lua o valoare aparținând intervalului . Construiți grafice ale funcțiilor și .km, km. Determinați probabilitatea de două lovituri asupra țintei.

1. Vorbitorii trebuie să vorbească la ședință DAR, LA, DIN, D. În câte moduri pot fi plasate pe lista de vorbitori astfel încât LA a vorbit după vorbitor DAR?
2. În câte moduri pot fi plasate 14 bile identice în 8 cutii?
3. Câte numere din cinci cifre pot fi făcute din numerele de la 1 la 9?
4. Elevul a venit la examen știind doar 24 din cele 32 de întrebări ale programului. Examinatorul i-a pus 3 întrebări. Găsiți probabilitatea ca elevul să răspundă la toate întrebările.
5. Până la sfârșitul zilei, în magazin au mai rămas 60 de pepeni, inclusiv 50 copți. Clientul alege 2 pepeni verzi. Care este probabilitatea ca ambii pepeni verzi să fie copți?
6. În lotul de sportivi sunt 20 de alergători, 6 săritori și 4 aruncători de ciocane. Probabilitatea ca norma maestrului sportului să fie îndeplinită de un alergător este de 0,9; săritor - 0,8 și aruncător - 0,75. Determinați probabilitatea ca un atlet numit aleatoriu să îndeplinească standardul maestrului sportului.
7. Probabilitatea ca un articol închiriat să fie returnat în stare bună este de 0,8. Determinați probabilitatea ca din cinci lucruri luate: a) trei să fie returnate în stare bună; b) toate cele cinci articole vor fi returnate intacte; c) cel puțin două articole vor fi returnate intacte.
8. Probabilitatea unui defect într-un lot de 500 de piese este de 0,035. Determinați numărul cel mai probabil de piese defecte din acest lot.
9. În producția de becuri electrice, probabilitatea de fabricare a unei lămpi de clasa întâi se presupune a fi de 0,64. Determinați probabilitatea ca din 100 de lămpi electrice alese aleatoriu, 70 să fie de clasa întâi.
10. 400 de probe de minereu sunt supuse examinării. Probabilitatea de conținut de metal industrial în fiecare probă este aceeași și egală cu 0,8. Găsiți probabilitatea ca numărul de mostre cu conținut de metal industrial să fie între 290 și 340.
11. Este dată legea distribuției unei variabile aleatoare discrete X dacă X Xși ; 4) aflați dacă aceste cantități sunt dependente.
1. În câte moduri pot fi așezați 8 invitați la o masă rotundă, astfel încât doi invitați celebri să stea unul lângă altul?
2. Câte „cuvinte” diferite se pot forma prin rearanjarea literelor cuvântului „combinatoric”?
3. Câte triunghiuri sunt ale căror laturi iau una dintre următoarele valori: 4, 5, 6, 7 cm?
4. Literele alfabetului divizat sunt în plic: O, P, R, DIN, T. Literele sunt amestecate cu grijă. Determinați probabilitatea ca, scoțând aceste litere și punându-le una lângă alta, să obțineți cuvântul " SPORTUL‘.
5. De la prima mașină, 20% merg la montaj, de la a doua 30%, de la a treia - 50% din piese. Prima mașină oferă o medie de 0,2% din defecte, a doua - 0,3%, a treia - 1%. Găsiți probabilitatea ca piesa primită pentru asamblare să fie defectă.
6. Unul dintre cei trei trăgători este chemat pe linia de foc și trage un foc. Ținta este lovită. Probabilitatea de a lovi ținta cu o singură lovitură pentru primul trăgător este de 0,3, pentru al doilea - 0,5, pentru al treilea - 0,8. Găsiți probabilitatea ca focul să fi fost tras de al doilea trăgător.
7. În atelier sunt 6 motoare. Pentru fiecare motor, probabilitatea ca acesta să fie pornit în prezent este de 0,8. Aflați probabilitatea ca în acest moment: a) 4 motoare să fie pornite; b) cel puțin un motor este pornit; c) toate motoarele sunt pornite.
8. Televizorul are 12 lămpi. Fiecare dintre ele cu o probabilitate de 0,4 poate eșua în perioada de garanție. Găsiți numărul cel mai probabil de lămpi care s-au defectat în perioada de garanție.
9. Probabilitatea de a avea un băiat este de 0,515. Aflați probabilitatea ca din 200 de copii născuți băieți și fete să fie împărțiți în mod egal.
10. Probabilitatea ca piesa să nu fi trecut de verificarea Departamentului de control al calității va fi de . Găsiți probabilitatea ca 70 până la 100 de părți să fie nebifate dintre 400 de părți alese aleatoriu.
11. Este dată legea distribuției unei variabile aleatoare discrete X:
- Principalele legi ale distribuției unei variabile aleatoare Instituția de învățământ „Departamentul de Stat de Matematică Superioară din Belarus” pentru studiul temei „Legile de bază ale distribuției unei variabile aleatoare” de către studenții facultății de contabilitate forma de absent care primesc educație (NISPO) Principalele legi ale distribuției aleatorii […]
- Amenzile poliției rutiere leninogorsk Întârziere, statul va lua măsuri pentru a vă colecta amenzile dacă nu ați făcut apel la amenzile poliției rutiere leninogorsk aveți nevoie de simboluri. Fără acte de înregistrare și fără o politică OSAGO, un hyperlink către acest articol va costa 500 de locuri. Pedepsele oficiale ale poliției rutiere leninogorsk […]
- Indemnizație de încetare pentru Cernobîl: (3 + 1) sau doar 3? Pentru cetățenii afectați de Dezastrul de la Cernobîl(în continuare - victime de la Cernobîl), Legea nr. 796 * stabilește anumite beneficii și garanții. Astfel, supraviețuitorii de la Cernobîl clasificați în categoria 1, printre altele, sunt definiți prin Legea menționată ca având un drept preferențial la […]
- Taxa Dacha. Ar trebui să știi. Eu și soțul meu ne gândim la o casă de vară unde să venim, să săpăm puțin în paturi, iar seara să stăm pe un balansoar lângă foc și să nu ne gândim la nimic. Relaxeaza-te. Știm direct că horticultura și horticultura sunt scumpe (balegar de grajd, îngrășăminte, răsaduri), taxe... Ce […]
- Sfat 1: Cum să determinați legea distribuției Cum să determinați legea distribuției Cum să construiți o diagramă Pareto Cum să găsiți așteptarea matematică dacă varianța este cunoscută - o referință matematică; - un creion simplu; - caiet; - un stilou. Legea distribuției normale în 2018 Sfatul 2: Cum să […]
- 3. VALORI ALEATORII. CONCEPTUL DE VARIABILĂ ALEATORIE O variabilă aleatoare este o variabilă care, în urma unor teste efectuate în aceleași condiții, ia valori diferite, în general, care depind de factori aleatori care nu sunt luați în considerare. Exemple de variabile aleatoare: numărul de puncte scăzut pe […]
- Pasaj de lichidare Stot - suprafața totală a obiectului, km 2; N apoi - numărul de elemente afectate ale obiectului (cladiri, ateliere, structuri, sisteme); Ntotal - numărul total de elemente ale obiectului. Următoarea expresie poate fi folosită pentru a determina numărul de victime: unde Spor este numărul de victime într-o explozie bruscă; Lc este numărul de angajați ai acestui […]
- Legile radiațiilor lui Stefan Boltzmann Pentru corpurile reale legea Stefan-Boltzmann se îndeplinește doar calitativ, adică odată cu creșterea temperaturii, luminozitățile energetice ale tuturor corpurilor cresc. Totuși, pentru corpurile reale, dependența luminozității energiei de temperatură nu mai este descrisă printr-o relație simplă (16.7), ci […]
Luați în considerare distribuțiile discrete care sunt adesea utilizate în sistemele de servicii de modelare.
distribuția Bernoulli. Schema Bernoulli este o succesiune de studii independente, în fiecare dintre ele sunt posibile doar două rezultate - „succes” și „eșec” cu probabilități. Rși q = 1 - R. Fie variabila aleatoare X poate lua două valori cu probabilități corespunzătoare:
Funcția de distribuție Bernoulli are forma
Graficul său este prezentat în Fig. 11.1.
O variabilă aleatorie cu o astfel de distribuție este egală cu numărul de succese dintr-o încercare a schemei Bernoulli.
Funcția generatoare, conform (11.1) și (11.15), se calculează ca
Orez. 11.1.

Folosind formula (11.6), găsim așteptările matematice ale distribuției:
Calculăm derivata a doua a funcției generatoare conform (11.17)
Prin (11.7) obținem varianța distribuției
Distribuția Bernoulli joacă mare rolîn teoria serviciului de masă, fiind un model al oricărui experiment aleatoriu, ale cărui rezultate aparțin a două clase care se exclud reciproc.
Distribuția geometrică. Să presupunem că evenimentele au loc în momente discrete timp independent unul de celălalt. Probabilitatea ca un eveniment să se producă este R, iar probabilitatea ca aceasta să nu se întâmple este q = 1-p, De exemplu, un client care a venit să plaseze o comandă.
Notează prin r la probabilitatea ca un eveniment să se producă prima dată la un moment dat la, acestea. la-al-lea client a făcut o comandă, iar precedentul la- 1 fără clienți. Atunci probabilitatea acestui eveniment complex poate fi determinată de teorema înmulțirii probabilităților evenimentelor independente
Probabilitățile evenimentelor cu distribuție geometrică sunt prezentate în fig. 11.2.
Suma probabilităților tuturor evenimentelor posibile
este o progresie geometrică, deci distribuția se numește geometric. Din moment ce (1 - R)

Valoare aleatoare Xs distribuția geometrică are semnificația numărului primei încercări reușite din schema Bernoulli.

Orez. 11.2.
Determinați probabilitatea ca un eveniment să se producă pentru X>k

și funcția de distribuție geometrică

Să calculăm funcția generatoare a distribuției geometrice conform (11.1) și (11.20)
așteptarea matematică a distribuției geometrice conform (11.6)
iar dispersia conform (11.7)

Distribuția geometrică este considerată a fi o versiune discretă a distribuției exponențiale continue și are, de asemenea, o serie de proprietăți utile pentru modelarea sistemelor de servicii. În special, ca și distribuția exponențială, distribuția geometrică nu are memorie:

acestea. dacă / experimentele eșuate, atunci probabilitatea ca pentru primul succes este necesar să se efectueze mai mult j de noi încercări este aceeași cu probabilitatea ca o nouă serie de încercări să necesite un prim succes. /" încercări. Cu alte cuvinte, încercările anterioare nu au niciun efect asupra încercărilor viitoare și încercările sunt independente. Adesea acest lucru este adevărat. și se fac ordine. la întâmplare.
Să luăm în considerare un exemplu de sistem ai cărui parametri de funcționare sunt supuși unei distribuții geometrice.
Stăpânul are la dispoziție P piese de schimb identice. Fiecare detaliu este probabil q are un defect. În timpul reparației, piesa este instalată în dispozitiv, care este verificată pentru funcționare. Dacă dispozitivul nu funcționează, atunci piesa este înlocuită cu alta. Considerăm o variabilă aleatoare X- numarul de piese de verificat.
Probabilitățile numărului de piese testate vor avea valorile prezentate în tabel:
|
rya"~ x |
Aici q = 1 - R.
Aşteptarea matematică a numărului de piese verificate este definită ca

Distribuție binomială. Luați în considerare o variabilă aleatoare
Unde Xj respectă distribuția Bernoulli cu parametrul Rși variabile aleatoare Xj independent.
Valoare aleatoare X va fi egal cu numărul de apariții ale unităților la P teste, adică o variabilă aleatoare cu distribuție binomială are semnificația numărului de succese în P teste independente.
Conform (11.9), funcția generatoare a sumei variabilelor aleatoare independente reciproc, fiecare dintre ele având o distribuție Bernoulli, este egală cu produsul funcțiilor lor generatoare (11.17):
Expandând funcția generatoare (11.26) într-o serie, obținem

În conformitate cu definiția funcției generatoare (11.1), probabilitatea ca variabila aleatoare X va prelua sensul la:
Unde  sunt coeficienți binomi.
sunt coeficienți binomi.
11deoarece și unități per P locurile pot fi aranjate în moduri C*, apoi numărul de mostre care conțin la unitățile vor fi, evident, aceleași.
Funcția de distribuție pentru legea binomială este calculată prin formula
Distribuția este numită binom datorită faptului că probabilitățile în formă sunt termeni ai expansiunii binomului:

Este clar că probabilitatea totală a tuturor rezultatelor posibile este egală cu 1:

Din (11.29) se pot obține o serie de proprietăți utile ale coeficienților binomi. De exemplu, când R =1, q=1 obținem
Dacă punem R =1, q= - 1 , atunci
Pentru orice 1k sunt valabile următoarele relații:
Probabilitățile ca în P teste, evenimentul va avea loc: 1) mai puțin de × încă 2 la o singura data; 3) cel puțin &ori; 4) nu mai mult de & ori, găsiți, respectiv, conform formulelor: 
Folosind (11.6), definim așteptarea distribuției binomiale
iar conform (11.7) - dispersie: 
Să luăm în considerare câteva exemple de sisteme ai căror parametri de funcționare sunt descriși de distribuția binomială.
1. Un lot de 10 produse conține unul non-standard. Să găsim probabilitatea ca, cu un eșantion aleatoriu de 5 produse, toate să fie standard (eveniment DAR).
Numărul tuturor probelor aleatorii p - S, e 0 , iar numărul de mostre care favorizează evenimentul este P= C 9 5 . Astfel, probabilitatea dorită este egală cu

2. La intrarea într-un apartament nou, 2 la lămpi electrice noi. Fiecare lampă electrică se stinge în timpul anului cu o probabilitate R. Să găsim probabilitatea ca în cursul anului cel puțin jumătate din lămpile aprinse inițial să fie înlocuite cu altele noi (evenimentul DAR):

3. O persoană aparținând unui anumit grup de consumatori preferă produsul 1 cu o probabilitate de 0,2, produsul 2 cu o probabilitate de 0,3, produsul 3 cu o probabilitate de 0,4, produsul 4 cu o probabilitate de 0,1.Un grup de 6 consumatori. Găsiți probabilitățile următoarelor evenimente: DAR - grupul include cel puțin 4 consumatori care preferă produsul 3; LA- există cel puțin un consumator în grup care preferă produsul 4.
Aceste probabilități sunt:
Pentru mari /? calculele de probabilitate devin greoaie, deci se folosesc teoreme limită.
Teorema Laplace locală, conform căreia probabilitatea R p (k) este determinat de formula
Unde  - functia gaussiana;
- functia gaussiana; 
Teorema integrală a Laplace folosit pentru a calcula probabilitatea ca P teste independente, evenimentul va avea loc cel puțin la ( o dată și nu mai mult la 2 o singura data:
Să luăm în considerare exemple de utilizare a acestor teoreme.
1. Atelierul de cusut produce haine pe masura, dintre care 90% sunt de cea mai buna calitate. Găsiți probabilitatea ca între 200 de produse să fie cel puțin 160 și cel mult 170 de cea mai bună calitate.
Soluţie: 
2. O companie de asigurări are 12.000 de clienți. Fiecare dintre ei, asigurându-se împotriva unui accident, contribuie cu 10 mii de ruble. Probabilitatea unui accident R - 0,006 și plata către victimă a 1 milion de ruble. Să aflăm profitul companiei de asigurări, prevăzut cu o probabilitate de 0,995; cu alte cuvinte, la ce profit se poate aștepta compania de asigurări la un nivel de risc de 0,005.
Soluție: Contribuția totală a tuturor clienților este de 12.000-10.000 = 120 de milioane de ruble. Profitul companiei depinde de număr la accidente și este determinată de egalitatea R = 120.000-1000 /: mii de ruble.
Prin urmare, este necesar să se găsească un astfel de număr A/ încât probabilitatea evenimentului P(k > M) nu a depășit 0,005. Apoi, cu o probabilitate de 0,995, profitul va fi furnizat R = 120.000-10.004 / mie de ruble.
Inegalitate P(k > M) P(k0.995. Din moment ce la > 0, atunci R( 0 0,995. Pentru a estima această probabilitate, folosim teorema integrală Laplace pentru P- 12.000 și /?=0,006, #=0,994:

Pentru că*! F(x]) = -0,5.
Astfel, este necesar să se găsească A/ pentru care
Găsim (M- 72)/8,5 > 2,58. Prin urmare, M>12 + 22 = 94.
Deci, cu o probabilitate de 0,995, compania garantează un profit
Este adesea necesar să se determine numărul cel mai probabil la 0. Probabilitatea unui eveniment cu un număr de succese la 0 depășește sau cel puțin nu mai puțin decât probabilitatea altor rezultate posibile ale testului. Numărul cel mai probabil la 0 determinată din dubla inegalitate
3. Să fie 25 de mostre de bunuri de larg consum. Probabilitatea ca fiecare dintre probe să fie acceptabilă pentru client este de 0,7. Este necesar să se determine numărul cel mai probabil de mostre care vor fi acceptabile pentru clienți. Până la (11.39)

De aici la 0 - 18.
Distribuția Poisson. Distribuția Poisson determină probabilitatea ca, având în vedere un număr foarte mare de încercări, P,în fiecare dintre care probabilitatea unui eveniment R foarte mic, evenimentul se va întâmpla exact la schz.
Lasă treaba pr \u003d k; aceasta înseamnă că numărul mediu de apariții ale unui eveniment în diferite serii de încercări, i.e. la diverse P, ramane neschimbat. În acest caz, distribuția Poisson poate fi utilizată pentru a aproxima distribuția binomială:

Din moment ce pentru mare P 
Funcția generatoare a distribuției Poisson se calculează din (11.1) ca
unde prin formula Maclaurin
În conformitate cu proprietatea coeficienților funcției generatoare, probabilitatea de apariție la succese cu un număr mediu de succese X se calculează ca (11,40).
Pe fig. 11.3 arată densitatea de probabilitate a distribuției Poisson.
Funcția generatoare a distribuției Poisson poate fi obținută și folosind extinderea în serie a funcției generatoare a distribuției binomiale pentru pr \u003d X la P-» oo și formula Maclaurin (11.42):

Orez. 11.3.
Definim așteptarea matematică prin (11.6)
iar dispersia conform (11.7)

Luați în considerare un exemplu de sistem cu o distribuție Poisson a parametrilor.
Compania a trimis 500 de produse la magazin. Probabilitatea de deteriorare a produsului în timpul transportului este de 0,002. Găsiți probabilitățile ca produsele să fie deteriorate în timpul tranzitului: exact 3 (evenimentul R); mai puțin de 3 (eveniment LA) mai mult de 3 (eveniment Q; cel puțin unul (eveniment D).
Număr P= 500 este mare, probabilitate R= 0,002 este mic, evenimentele considerate (deteriorarea produsului) sunt independente, deci se poate folosi formula Poisson (11,40).
La x=pr= 500 0,002=1 obținem:

Distribuția Poisson are o serie de proprietăți utile pentru modelarea sistemelor de servicii.
1. Suma variabilelor aleatoare X \u003d X ( + X 2 cu o distribuție Poisson este de asemenea distribuită conform legii lui Poisson.
Dacă variabilele aleatoare au funcții generatoare:
atunci, conform (11.9), funcția generatoare a sumei variabilelor aleatoare independente cu distribuție Poisson va avea forma:
Parametrul distribuției rezultate este X x + X 2.
2. Dacă numărul de elemente./V al mulţimii se supune distribuţiei Poisson cu parametrul X iar fiecare element este ales independent cu probabilitate R, apoi elementele eșantionului de dimensiune Y distribuit conform legii Poisson cu parametrul pX.
Lăsa ![]() , Unde
, Unde ![]() corespunde distribuției Bernoulli și N- Distribuția Poisson. Funcțiile generatoare corespunzătoare, conform (11.17), (11.41):
corespunde distribuției Bernoulli și N- Distribuția Poisson. Funcțiile generatoare corespunzătoare, conform (11.17), (11.41):
Funcția generatoare a unei variabile aleatoare Y se calculează conform (11.14)
acestea. funcția generatoare corespunde distribuției Poisson cu parametrul pX.
3. Ca o consecință a proprietății 2, este valabilă următoarea proprietate. Dacă numărul de elemente ale mulţimii este distribuit conform legii Poisson cu parametrul X iar mulțimea este distribuită aleatoriu cu probabilități /?, și p 2 = 1 - Rîn două grupuri, atunci dimensiunile seturilor sunt 7V și N 2 sunt independente și Poisson-distribuite cu parametri p(kși p(k.
Pentru ușurință în utilizare, vă prezentăm rezultatele obținute cu privire la distribuții discrete sub forma unui tabel. 11.1 și 11.2.
Tabelul 11.1. Principalele caracteristici ale distribuțiilor discrete
|
Distributie |
Densitate |
Gamă |
Opțiuni |
tn | |
C X--2 |
|
|
Bernoulli |
P(X = ) = p P (X = 0} = R + Z= 1 |
P - 0,1 |
||||
|
Geometric |
p(-p) la -1 |
k = 1,2,... |
^ 1 1 | |
1 -R |
||
|
Binom |
cu la p la (- R g la |
* = 1,2,...,#" |
pr( - p) |
1 -r pr |
||
|
Poisson |
E la! |
k = 1,2,... |
Tabelul 11. 2. Funcții generatoare ale distribuțiilor discrete
ÎNTREBĂRI DE TEST
- 1. Ce distribuții de probabilitate sunt clasificate ca fiind discrete?
- 2. Ce este o funcție generatoare și pentru ce este folosită?
- 3. Cum se calculează momentele variabilelor aleatoare folosind funcția generatoare?
- 4. Care este funcția generatoare a sumei variabilelor aleatoare independente?
- 5. Ce se numește distribuție compusă și cum se calculează funcțiile generatoare ale distribuțiilor compozite?
- 6. Prezentați principalele caracteristici ale distribuției Bernoulli, oferiți un exemplu de utilizare a acesteia în sarcini de serviciu.
- 7. Dați principalele caracteristici ale distribuției geometrice, dați un exemplu de utilizare în sarcini de serviciu.
- 8. Dați principalele caracteristici ale distribuției binomiale, dați un exemplu de utilizare în sarcini de serviciu.
- 9. Prezentați principalele caracteristici ale distribuției Poisson, oferiți un exemplu de utilizare a acesteia în sarcini de serviciu.
Definiția 3. X are legea distribuției normale (legea Gauss), dacă densitatea sa de distribuție are forma:
Unde m = M(X), σ 2=D(X), σ > 0 .
Curba de distribuție normală se numește curba normala sau gaussiana(Fig. 6.7).
O curbă normală este simetrică față de o linie dreaptă x = m, are un maxim la punct x = m, egal .
Funcția de distribuție a unei variabile aleatoare X, distribuită conform legii normale, se exprimă în termenii funcției Laplace Ф( X) conform formulei:
F( X) este funcția Laplace.
Cometariu. Funcția F( X) este impar (Ф(- X) = -Ф( X)), în plus, când X> 5 poate fi considerat F( X) ≈ 1/2.
Tabelul cu valorile funcției Ф( X) este dat în anexă (Tabelul P 2.2).
Graficul funcției de distribuție F(X) este prezentată în fig. 6.8.
Probabilitatea ca o variabilă aleatoare X să ia valori aparținând intervalului ( a;b) se calculează prin formula:
R(A< X < b ) = .
Probabilitatea ca valoarea absolută a abaterii unei variabile aleatoare de la așteptările ei matematice să fie mai mică decât un număr pozitiv δ este calculată prin formula:
P(| X -m| .
În special, când m=0 egalitatea este adevărată:
P(| X | .
„Regula celor trei sigma”
Dacă variabila aleatoare X are o lege de distribuție normală cu parametri mși σ, atunci este aproape sigur că valorile sale sunt conținute în intervalul ( m 3σ; m+ 3σ), deoarece P(| X -m| = 0,9973.
Problema 6.3. Valoare aleatoare X distribuit normal cu media 32 și varianța 16. Aflați: a) densitatea distribuției probabilităților f(X); X va lua o valoare din intervalul (28;38).
Soluţie: După condiție m= 32, σ 2 = 16, prin urmare, σ= 4, atunci
A)
b) Să folosim formula:
R(A< X )= .
Înlocuind A= 28, b= 38, m= 32, σ= 4, obținem
R(28< X < 38)= F(1,5) F(1)
Conform tabelului de valori al funcției Ф( X) găsim Ф(1,5) = 0,4332, Ф(1) = 0,3413.
Deci probabilitatea dorită este:
P(28 Sarcini 6.1.
Valoare aleatoare X distribuite uniform în intervalul (-3;5). Găsi: a) densitatea distribuţiei f(X);
b) funcţii de distribuţie F(X);
c) caracteristici numerice; d) probabilitate R(4<X<6). 6.2.
Valoare aleatoare X distribuite uniform pe segment. Găsi: a) densitatea distribuţiei f(X);
b) funcţia de distribuţie F(X);
c) caracteristici numerice; d) probabilitate R(3≤X≤6). 6.3.
Pe autostradă este instalat un semafor automat, în care semaforul verde este aprins 2 minute, galben 3 secunde și roșu 30 secunde etc. O mașină circulă pe autostradă la un moment dat. Găsiți probabilitatea ca mașina să treacă de semafor fără să se oprească. 6.4.
Trenurile de metrou circulă regulat la intervale de 2 minute. Pasagerul intră pe platformă la un moment dat. Care este probabilitatea ca pasagerul să fie nevoit să aștepte mai mult de 50 de secunde pentru tren? Aflați așteptările matematice ale unei variabile aleatorii X- timpul de așteptare a trenului. 6.5.
Aflați varianța și abaterea standard a distribuției exponențiale date de funcția de distribuție: 6.6.
Variabilă aleatoare continuă X dat de densitatea distribuției de probabilitate: a) Numiți legea distribuției variabilei aleatoare considerate. b) Aflați funcția de distribuție F(X) și caracteristicile numerice ale variabilei aleatoare X. 6.7.
Valoare aleatoare X distribuite conform legii exponențiale, dată de densitatea distribuției de probabilitate: X va lua o valoare din intervalul (2,5;5). 6.8.
Variabilă aleatoare continuă X distribuite conform legii exponențiale date de funcția de distribuție: Găsiți probabilitatea ca în urma testului X va lua valoarea din intervalul . 6.9.
Așteptările matematice și abaterea standard a unei variabile aleatoare distribuite normal sunt 8 și, respectiv, 2. Aflați: a) densitatea distribuție f(X); b) probabilitatea ca în urma testului X va lua o valoare din intervalul (10;14). 6.10.
Valoare aleatoare X distribuit normal cu medie 3,5 și varianță 0,04. Găsi: a) densitatea distribuţiei f(X); b) probabilitatea ca în urma testului X va lua valoarea din intervalul . 6.11.
Valoare aleatoare X distribuite normal cu M(X) =
0 și D(X)=
1. Care dintre evenimente: | X|≤0,6 sau | X|≥0,6 are o probabilitate mare? 6.12.
Valoare aleatoare X distribuite normal cu M(X) =
0 și D(X)=
1. Din ce interval (-0,5; -0,1) sau (1; 2) dintr-un test va lua o valoare cu o probabilitate mai mare? 6.13.
Prețul curent pe acțiune poate fi modelat folosind distribuția normală cu M(X)=
10 zile unitati și σ( X) = 0,3 den. unitati Găsi: a) probabilitatea ca prețul actual al acțiunii să fie de la 9,8 den. unitati până la 10,4 den. unități; b) folosind „regula celor trei sigma” pentru a găsi limitele în care se va afla prețul curent al acțiunii. 6.14.
Se cântărește substanța fără erori sistematice. Erorile de cântărire aleatoare sunt supuse legii normale cu abaterea standard σ= 5r. Aflați probabilitatea ca în patru experimente independente eroarea în trei cântăriri să nu depășească 3 g în valoare absolută. 6.15.
Valoare aleatoare X distribuite normal cu M(X)= 12.6. Probabilitatea ca o variabilă aleatoare să cadă în intervalul (11,4; 13,8) este 0,6826. Găsiți abaterea standard σ. 6.16.
Valoare aleatoare X distribuite normal cu M(X) = 12 și D(X) = 36. Aflați intervalul în care, cu o probabilitate de 0,9973, variabila aleatoare va cădea în urma testului X. 6.17.
O piesă produsă de o mașină automată este considerată defectă în cazul abaterii X parametrul său controlat din valoarea nominală depășește cu modulo 2 unități de măsură. Se presupune că variabila aleatoare X distribuite normal cu M(X) = 0 și σ( X) = 0,7. Ce procent de piese defecte emite mașina? 3.18.
Parametru X părțile sunt distribuite în mod normal cu o așteptare matematică de 2 egală cu valoarea nominală și o abatere standard de 0,014. Găsiți probabilitatea ca abaterea X din valoarea nominală modulo nu va depăși 1% din valoarea nominală. Răspunsuri în) M(X)=1, D(X)=16/3, σ( X)= 4/ , d)1/8. în) M(X)=4,5, D(X) =2 , σ ( X)= , d)3/5. 6.3.
40/51. 6.4.
7/12, M(X)=1. 6.5.
D(X) = 1/64, σ ( X)=1/8 6.6.
M(X)=1 , D(X) =2 , σ ( X)= 1 . 6.7.
P(2,5<X<5)=e -1 e -2 ≈0,2325 6.8.
Р(2≤ X≤5)=0,252. b) R(10 < X < 14) ≈ 0,1574. b) R(3,1 ≤ X ≤ 3,7) ≈ 0,8185. 6.11.
|X|≥0,6. 6.12.
(-0,5; -0,1). 6.13.
a) Р(9,8 ≤ Х ≤ 10,4) ≈ 0,6562 6.14.
0,111. b) (9,1; 10,9). 6.15.
σ = 1,2. 6.16.
(-6; 30). 6.17.
0,4 %. - numarul de baieti din 10 nou-nascuti. Este destul de clar că acest număr nu este cunoscut în prealabil, iar în următorii zece copii născuți pot exista: Sau băieți - unul si numai unul dintre opțiunile enumerate. Și, pentru a fi în formă, puțină educație fizică: - distanta de saritura in lungime (în unele unități). Nici măcar maestrul sportului nu este în stare să prevadă :) Totuși, care sunt ipotezele tale? 2) Variabilă aleatoare continuă - ia toate valori numerice dintr-un interval finit sau infinit. Notă
: abrevierile DSV și NSV sunt populare în literatura educațională Mai întâi, să analizăm o variabilă aleatoare discretă, apoi - continuu. - aceasta este conformitateîntre valorile posibile ale acestei mărimi și probabilitățile acestora. Cel mai adesea, legea este scrisă într-un tabel: Si acum punct foarte important: din moment ce variabila aleatoare neapărat voi accepta una dintre valori, apoi se formează evenimentele corespunzătoare grup complet iar suma probabilităților apariției lor este egală cu unu: sau, dacă este scris pliat: Deci, de exemplu, legea distribuției probabilităților punctelor de pe un zar are următoarea formă: Fără comentarii. Este posibil să aveți impresia că o variabilă aleatoare discretă poate lua doar valori întregi „bune”. Să risipim iluzia - pot fi orice: Exemplul 1 Unele jocuri au următoarea lege de distribuire a plăților: …probabil că visezi la astfel de sarcini de multă vreme :) Hai să-ți spun un secret – și eu. Mai ales după terminarea lucrărilor teoria câmpului. Soluţie: deoarece o variabilă aleatoare poate lua doar una din trei valori, se formează evenimentele corespunzătoare grup complet, ceea ce înseamnă că suma probabilităților lor este egală cu unu: Îl expunem pe „partizanul”: Control: de ce ai nevoie pentru a te asigura. Răspuns: Nu este neobișnuit când legea distribuției trebuie elaborată independent. Pentru această utilizare definiția clasică a probabilității, teoreme de înmulțire/adunare pentru probabilitățile de evenimenteși alte chips-uri tervera: Exemplul 2 În cutie sunt 50 de bilete de loterie, dintre care 12 sunt câștigătoare, iar 2 dintre ele câștigă 1000 de ruble fiecare, iar restul - 100 de ruble fiecare. Întocmește o lege de distribuție a unei variabile aleatoare - mărimea câștigurilor, dacă un bilet este extras aleatoriu din casetă. Soluţie: după cum ați observat, este obișnuit să plasați valorile unei variabile aleatoare în ordine crescătoare. Prin urmare, începem cu cele mai mici câștiguri, și anume ruble. În total, sunt 50 - 12 = 38 de astfel de bilete, iar conform definiție clasică: Restul cazurilor sunt simple. Probabilitatea de a câștiga ruble este: Verificarea: - si acesta este un moment deosebit de placut al unor astfel de sarcini! Răspuns: legea impusă de distribuire a plăților: Următoarea sarcină pentru o decizie independentă: Exemplul 3 Probabilitatea ca trăgătorul să lovească ținta este de . Faceți o lege de distribuție pentru o variabilă aleatorie - numărul de lovituri după 2 lovituri. ... Stiam ca ti-a fost dor de el :) Ne amintim teoreme de înmulțire și adunare. Soluție și răspuns la sfârșitul lecției. Legea distribuției descrie complet o variabilă aleatoare, dar în practică este util (și uneori mai util) să cunoști doar o parte din ea. caracteristici numerice
. În termeni simpli, asta valoarea medie aşteptată cu teste repetate. Lasă o variabilă aleatorie să ia valori cu probabilități sau în formă pliată: Să calculăm, de exemplu, așteptarea matematică a unei variabile aleatoare - numărul de puncte aruncate pe un zar: Acum să ne amintim jocul nostru ipotetic: Apare întrebarea: este chiar profitabil să joci acest joc? ... cine are impresii? Așa că nu poți spune „de la îndemână”! Dar la această întrebare se poate răspunde cu ușurință prin calcularea așteptărilor matematice, în esență - medie ponderată probabilități de câștig: Astfel, așteptările matematice ale acestui joc pierzând. Nu aveți încredere în impresii - aveți încredere în numere! Da, aici poți câștiga de 10 sau chiar de 20-30 de ori la rând, dar pe termen lung vom fi inevitabil ruinați. Și nu te-aș sfătui să joci astfel de jocuri :) Ei bine, poate doar pentru distractie. Din toate cele de mai sus, rezultă că așteptarea matematică NU este o valoare aleatorie. Sarcina creativă pentru cercetare independentă: Exemplul 4 Domnul X joacă la ruleta europeană după următorul sistem: pariază constant 100 de ruble pe roșu. Alcătuiți legea distribuției unei variabile aleatoare - profitul acesteia. Calculați așteptările matematice ale câștigurilor și rotunjiți-o la copeici. Cum in medie jucătorul pierde la fiecare sută de pariuri? Referinţă
: Ruleta europeană conține 18 sectoare roșii, 18 negre și 1 verde („zero”). În cazul unei căderi „roșii”, jucătorul este plătit cu un pariu dublu, în caz contrar, acesta merge la venitul cazinoului. Există multe alte sisteme de ruletă pentru care vă puteți crea propriile tabele de probabilitate. Dar acesta este cazul când nu avem nevoie de nicio lege și tabele de distribuție, deoarece este stabilit cu siguranță că așteptările matematice ale jucătorului vor fi exact aceleași. Doar modificări de la sistem la sistem După cum se știe, variabilă aleatorie
se numește o variabilă care poate lua anumite valori în funcție de caz. Variabilele aleatoare sunt notate cu majuscule ale alfabetului latin (X, Y, Z), iar valorile lor sunt notate cu litere mici corespunzătoare (x, y, z). Variabilele aleatoare sunt împărțite în discontinue (discrete) și continue. Variabilă aleatoare discretă
este o variabilă aleatorie care ia doar un set finit sau infinit (numărabil) de valori cu anumite probabilități diferite de zero. Legea distribuției unei variabile aleatoare discrete
este o funcție care conectează valorile unei variabile aleatoare cu probabilitățile corespunzătoare. Legea distribuției poate fi specificată în una din următoarele moduri. 1
. Legea distribuției poate fi dată de tabelul:
unde λ>0, k = 0, 1, 2, … . în) prin utilizarea funcția de distribuție F(x)
, care determină pentru fiecare valoare x probabilitatea ca variabila aleatoare X să ia o valoare mai mică decât x, adică. F(x) = P(X< x). Proprietățile funcției F(x) 3
. Legea distribuției poate fi stabilită grafic
– poligon de distribuție (poligon) (vezi problema 3). Rețineți că pentru a rezolva unele probleme nu este necesar să cunoașteți legea distribuției. În unele cazuri, este suficient să cunoașteți unul sau mai multe numere care reflectă cele mai importante caracteristici ale legii distribuției. Poate fi un număr care are semnificația „valorii medii” a unei variabile aleatoare sau un număr care arată dimensiunea medie a abaterii unei variabile aleatoare de la valoarea sa medie. Numerele de acest fel sunt numite caracteristici numerice ale unei variabile aleatorii. Caracteristicile numerice de bază ale unei variabile aleatoare discrete
: Au fost emise 1000 de bilete de loterie: 5 dintre ele câștigă 500 de ruble, 10 - 100 de ruble, 20 - 50 de ruble, 50 - 10 ruble. Determinați legea distribuției de probabilitate a variabilei aleatoare X - câștiguri pe bilet. Soluţie.
În funcție de starea problemei, sunt posibile următoarele valori ale variabilei aleatoare X: 0, 10, 50, 100 și 500. Numărul de bilete fără câștig este 1000 - (5+10+20+50) = 915, apoi P(X=0) = 915/1000 = 0,915. În mod similar, găsim toate celelalte probabilități: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01, P(X=0,01). =500) = 5/1000=0,005. Prezentăm legea rezultată sub forma unui tabel: Aflați așteptările matematice ale lui X: M(X) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1 + 2+3+4+5+6)/6 = 21/6 = 3,5 Dispozitivul este format din trei elemente de operare independentă. Probabilitatea de eșec a fiecărui element dintr-un experiment este de 0,1. Întocmește o lege de distribuție pentru numărul de elemente eșuate într-un experiment, construiește un poligon de distribuție. Găsiți funcția de distribuție F(x) și reprezentați-o grafic. Aflați așteptările matematice, varianța și abaterea standard a unei variabile aleatoare discrete. Soluţie.
1.
Variabila aleatorie discretă X=(numărul de elemente eșuate într-un experiment) are următoarele valori posibile: x 1 =0 (niciunul dintre elementele dispozitivului nu a eșuat), x 2 =1 (un element a eșuat), x 3 =2 ( două elemente au eșuat ) și x 4 \u003d 3 (trei elemente au eșuat). Eșecurile elementelor sunt independente unele de altele, probabilitățile de eșec ale fiecărui element sunt egale între ele, prin urmare, este aplicabil formula lui Bernoulli
. Având în vedere că, prin condiție, n=3, p=0,1, q=1-p=0,9, determinăm probabilitățile valorilor: Astfel, legea de distribuție binomială dorită X are forma: Pe axa absciselor, graficăm valorile posibile x i, iar pe axa ordonatelor, probabilitățile corespunzătoare p i . Să construim punctele M 1 (0; 0,729), M 2 (1; 0,243), M 3 (2; 0,027), M 4 (3; 0,001). Conectând aceste puncte cu segmente de linie, obținem poligonul de distribuție dorit. 3.
Găsiți funcția de distribuție F(x) = P(X Graficul funcției F(x) 4.
Pentru distribuția binomială X: Legea distribuției unei variabile aleatoare discrete

Termenul este destul de comun rând
distributie, dar în unele situații sună ambiguu și, prin urmare, voi respecta „legea”.

![]()
![]()
– astfel, probabilitatea de a câștiga unități convenționale este de 0,4.
este probabilitatea ca un bilet extras aleatoriu să nu câștige.![]()
Așteptările matematice ale unei variabile aleatoare discrete
![]() respectiv. Atunci așteptarea matematică a acestei variabile aleatoare este egală cu suma lucrărilor toate valorile sale după probabilitățile corespunzătoare:
respectiv. Atunci așteptarea matematică a acestei variabile aleatoare este egală cu suma lucrărilor toate valorile sale după probabilitățile corespunzătoare:![]()

Pentru distribuția binomială M(X)=np, pentru distribuția Poisson M(X)=λ
Pentru distribuția binomială D(X)=npq, pentru distribuția Poisson D(X)=λExemple de rezolvare a problemelor pe tema „Legea distribuției unei variabile aleatoare discrete”
Sarcina 1.
Sarcina 3.
P 3 (0) \u003d C 3 0 p 0 q 3-0 \u003d q 3 \u003d 0,9 3 \u003d 0,729;
P 3 (1) \u003d C 3 1 p 1 q 3-1 \u003d 3 * 0,1 * 0,9 2 \u003d 0,243;
P 3 (2) \u003d C 3 2 p 2 q 3-2 \u003d 3 * 0,1 2 * 0,9 \u003d 0,027;
P 3 (3) \u003d C 3 3 p 3 q 3-3 \u003d p 3 \u003d 0,1 3 \u003d 0,001;
Verificați: ∑p i = 0,729+0,243+0,027+0,001=1.
pentru 0< x ≤1 имеем F(x) = Р(Х<1) = Р(Х = 0) = 0,729;
pentru 1< x ≤ 2 F(x) = Р(Х<2) = Р(Х=0) + Р(Х=1) =0,729+ 0,243 = 0,972;
pentru 2< x ≤ 3 F(x) = Р(Х<3) = Р(Х = 0) + Р(Х = 1) + Р(Х = 2) = 0,972+0,027 = 0,999;
pentru x > 3 va fi F(x) = 1, deoarece evenimentul este sigur. 
- așteptarea matematică М(X) = np = 3*0,1 = 0,3;
- dispersia D(X) = npq = 3*0,1*0,9 = 0,27;
- abaterea standard σ(X) = √D(X) = √0,27 ≈ 0,52.