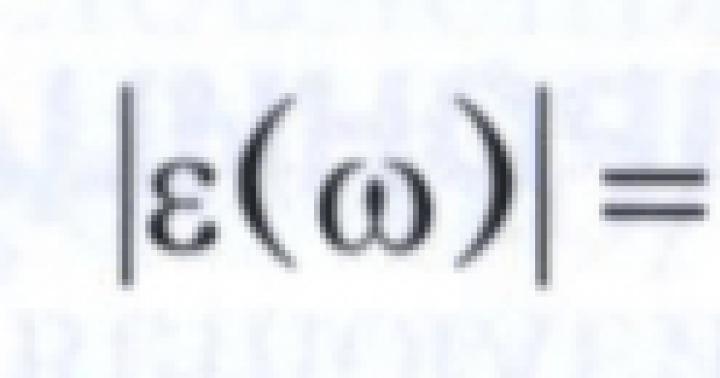Hotărâre majoritară probleme de matematică legate cumva de transformarea expresiilor numerice, algebrice sau funcționale. Acest lucru se aplică mai ales soluției. În variantele USE în matematică, acest tip de sarcină include, în special, sarcina C3. Învățarea cum să rezolvi sarcinile C3 este importantă nu numai pentru succes promovarea examenului, dar și pentru motivul că această abilitate este utilă atunci când studiezi un curs de matematică în învățământul superior.
Efectuând sarcinile C3, trebuie să decideți tipuri diferite ecuații și inegalități. Printre acestea se numără raționale, iraționale, exponențiale, logaritmice, trigonometrice, care conțin module (valori absolute), precum și combinate. Acest articol discută principalele tipuri de ecuații și inegalități exponențiale, precum și diverse metode deciziile lor. Citiți despre rezolvarea altor tipuri de ecuații și inegalități la rubrica „” în articolele dedicate metodelor de rezolvare a problemelor C3 din UTILIZAȚI opțiuni matematică.
Înainte de a trece la analiza specifice ecuații exponențiale și inegalități, în calitate de profesor de matematică, vă sugerez să periați unele dintre materialele teoretice de care vom avea nevoie.
Functie exponentiala
Ce este o funcție exponențială?
Funcția de vizualizare y = un x, Unde A> 0 și A≠ 1, numit functie exponentiala.
Principal proprietăți functie exponentiala y = un x:
Graficul unei funcții exponențiale
Graficul funcției exponențiale este expozant:
Grafice ale funcțiilor exponențiale (exponenți)
Rezolvarea ecuațiilor exponențiale
indicativ numite ecuații în care variabila necunoscută se găsește numai în exponenții oricăror puteri.
Pentru solutii ecuații exponențiale trebuie să cunoașteți și să puteți utiliza următoarea teoremă simplă:
Teorema 1. ecuație exponențială A f(X) = A g(X) (Unde A > 0, A≠ 1) este echivalentă cu ecuația f(X) = g(X).
În plus, este util să ne amintim formulele și acțiunile de bază cu grade:
Title="(!LANG:Redată de QuickLaTeX.com">!}
Exemplul 1 Rezolvați ecuația:
Decizie: utilizați formulele de mai sus și înlocuiți:
Ecuația devine atunci:
Discriminantul ecuației patratice rezultate este pozitiv:
Title="(!LANG:Redată de QuickLaTeX.com">!}
Aceasta înseamnă că această ecuație are două rădăcini. Le gasim:

Revenind la înlocuire, obținem:
![]()
A doua ecuație nu are rădăcini, deoarece funcția exponențială este strict pozitivă pe întregul domeniu de definiție. Să o rezolvăm pe a doua:
Ținând cont de cele spuse în teorema 1, trecem la ecuația echivalentă: X= 3. Acesta va fi răspunsul la sarcină.
Răspuns: X = 3.
Exemplul 2 Rezolvați ecuația:

Decizie: ecuația nu are restricții în ceea ce privește aria valorilor admisibile, deoarece expresia radicală are sens pentru orice valoare X(functie exponentiala y = 9 4 -X pozitiv și nu egal cu zero).
Rezolvăm ecuația prin transformări echivalente folosind regulile de înmulțire și împărțire a puterilor:
![]()
Ultima tranziție a fost efectuată în conformitate cu teorema 1.
Răspuns:X= 6.
Exemplul 3 Rezolvați ecuația:
![]()
Decizie: ambele părți ale ecuației inițiale pot fi împărțite la 0,2 X. Această tranziție va fi echivalentă, deoarece această expresie este mai mare decât zero pentru orice valoare X(funcția exponențială este strict pozitivă pe domeniul său). Atunci ecuația ia forma:
![]()
Răspuns: X = 0.
Exemplul 4 Rezolvați ecuația:
Decizie: simplificăm ecuația la una elementară prin transformări echivalente folosind regulile de împărțire și înmulțire a puterilor date la începutul articolului:
Împărțirea ambelor părți ale ecuației la 4 X, ca în exemplul anterior, este o transformare echivalentă, deoarece această expresie nu este egală cu zero pentru nicio valoare X.
Răspuns: X = 0.
Exemplul 5 Rezolvați ecuația:
![]()
Decizie: funcţie y = 3X, aflat în partea stângă a ecuației, este în creștere. Funcţie y = —X-2/3, stând în partea dreaptă a ecuației, este în scădere. Aceasta înseamnă că dacă graficele acestor funcții se intersectează, atunci cel mult la un moment dat. În acest caz, este ușor de ghicit că graficele se intersectează în punct X= -1. Nu vor exista alte rădăcini.
Răspuns: X = -1.
Exemplul 6 Rezolvați ecuația:
Decizie: simplificăm ecuația prin transformări echivalente, ținând cont peste tot că funcția exponențială este strict mai mare decât zero pentru orice valoare Xși folosind regulile de calcul al produsului și puterilor parțiale date la începutul articolului:
Răspuns: X = 2.
Rezolvarea inegalităților exponențiale
indicativ numite inegalităţi în care variabila necunoscută este cuprinsă numai în exponenţii unor puteri.
Pentru solutii inegalități exponențiale este necesară cunoașterea următoarei teoreme:
Teorema 2.În cazul în care un A> 1, apoi inegalitatea A f(X) > A g(X) este echivalentă cu o inegalitate de același sens: f(X) > g(X). Daca 0< A < 1, то показательное неравенство A f(X) > A g(X) este echivalentă cu o inegalitate de sens opus: f(X) < g(X).
Exemplul 7 Rezolvați inegalitatea:
Decizie: reprezentați inegalitatea inițială sub forma:
Împărțiți ambele părți ale acestei inegalități la 3 2 X, și (datorită pozitivității funcției y= 3 2X) semnul inegalității nu se va modifica:

Să folosim o înlocuire:
Atunci inegalitatea ia forma:
Deci, soluția inegalității este intervalul:
trecând la substituția inversă, obținem:
![]()
Inegalitatea din stânga, datorită pozitivității funcției exponențiale, este îndeplinită automat. Folosind proprietatea binecunoscută a logaritmului, trecem la inegalitatea echivalentă:

Deoarece baza gradului este un număr mai mare decât unu, echivalentul (prin teorema 2) va fi trecerea la următoarea inegalitate:
Așa că în sfârșit obținem Răspuns:
![]()
Exemplul 8 Rezolvați inegalitatea:
![]()
Decizie: folosind proprietățile înmulțirii și împărțirii puterilor, rescriem inegalitatea sub forma:
![]()
Să introducem o nouă variabilă:
Cu această înlocuire, inegalitatea ia forma:
![]()
Înmulțind numărătorul și numitorul fracției cu 7, obținem următoarea inegalitate echivalentă:
![]()
![]()
Deci, inegalitatea este satisfăcută de următoarele valori ale variabilei t:
![]()
Apoi, revenind la substituție, obținem:
![]()
Deoarece baza gradului aici este mai mare decât unu, este echivalent (prin teorema 2) să trecem la inegalitatea:
![]()
În sfârșit, obținem Răspuns:
![]()
Exemplul 9 Rezolvați inegalitatea:
Decizie:
Împărțim ambele părți ale inegalității prin expresia:
Este întotdeauna mai mare decât zero (deoarece funcția exponențială este pozitivă), astfel încât semnul inegalității nu trebuie schimbat. Primim:
t , care sunt în intervalul:
![]()
Trecând la substituția inversă, constatăm că inegalitatea inițială se împarte în două cazuri:

Prima inegalitate nu are soluții datorită pozitivității funcției exponențiale. Să o rezolvăm pe a doua:
Exemplul 10 Rezolvați inegalitatea:
Decizie:
Ramuri de parabolă y = 2X+2-X 2 sunt îndreptate în jos, deci este mărginit de sus de valoarea pe care o atinge la vârful său:
![]()
Ramuri de parabolă y = X 2 -2X+2, care se află în indicator, sunt direcționate în sus, ceea ce înseamnă că este limitat de jos de valoarea pe care o atinge în partea de sus:
![]()
În același timp, funcția se dovedește a fi mărginită de jos y = 3 X 2 -2X+2 în partea dreaptă a ecuației. Ea atinge cea mai mică valoare în același punct cu parabola din index, iar această valoare este egală cu 3 1 = 3. Deci, inegalitatea inițială poate fi adevărată numai dacă funcția din stânga și funcția din dreapta iau valoarea valoare , egală cu 3 (intersecția intervalelor acestor funcții este doar acest număr). Această condiție este îndeplinită într-un singur punct X = 1.
Răspuns: X= 1.
Pentru a învăța cum să rezolvi ecuații exponențiale și inegalități, trebuie să te antrenezi constant în soluția lor. În această problemă dificilă, diverse mijloace didactice, cărți de probleme la matematică elementară, culegeri de probleme competitive, ore de matematică la școală, precum și sesiuni individuale cu un tutore profesionist. Vă doresc din suflet succes în pregătirea dumneavoastră și rezultate strălucitoare la examen.
Serghei Valerievici
P.S. Dragi oaspeți! Vă rugăm să nu scrieți solicitări pentru rezolvarea ecuațiilor dvs. în comentarii. Din păcate, nu am timp deloc pentru asta. Astfel de mesaje vor fi șterse. Vă rugăm să citiți articolul. Poate că în el veți găsi răspunsuri la întrebări care nu v-au permis să vă rezolvați singur sarcina.
Mulți oameni cred că inegalitățile exponențiale sunt ceva atât de complicat și de neînțeles. Și că a învăța să le rezolvi este aproape o mare artă, pe care numai Aleșii sunt capabili să o înțeleagă...
Prostii complete! Inegalitățile exponențiale sunt ușoare. Și sunt întotdeauna ușor de rezolvat. Ei bine, aproape întotdeauna. :)
Astăzi vom analiza acest subiect pe larg. Această lecție va fi foarte utilă pentru cei care abia încep să înțeleagă această secțiune a matematicii școlare. Să începem cu sarcini simple și să trecem la probleme mai complexe. Astăzi nu va fi nimic, dar ceea ce veți citi acum va fi suficient pentru a rezolva majoritatea inegalităților pe toate tipurile de control și muncă independentă. Și la acest examen, de asemenea.
Ca întotdeauna, să începem cu o definiție. O inegalitate exponențială este orice inegalitate care conține o funcție exponențială. Cu alte cuvinte, poate fi întotdeauna redusă la o inegalitate a formei
\[((a)^(x)) \gt b\]
Unde rolul lui $b$ poate fi un număr obișnuit, sau poate ceva mai dur. Exemple? Da, te rog:
\[\begin(align) & ((2)^(x)) \gt 4;\quad ((2)^(x-1))\le \frac(1)(\sqrt(2));\ quad ((2)^(((x)^(2))-7x+14)) \lt 16; \\ & ((0,1)^(1-x)) \lt 0,01;\quad ((2)^(\frac(x)(2))) \lt ((4)^(\frac (4) )(X))). \\\end(align)\]
Cred că sensul este clar: există o funcție exponențială $((a)^(x))$, este comparată cu ceva și apoi i se cere să găsească $x$. În cazuri mai ales clinice, în locul variabilei $x$, pot pune o funcție $f\left(x \right)$ și astfel pot complica puțin inegalitatea. :)
Desigur, în unele cazuri, inegalitatea poate părea mai gravă. De exemplu:
\[((9)^(x))+8 \gt ((3)^(x+2))\]
Sau chiar asta:
În general, complexitatea unor astfel de inegalități poate fi foarte diferită, dar până la urmă ele se rezumă totuși la o construcție simplă $((a)^(x)) \gt b$. Și ne vom ocupa cumva de un astfel de design (în special în cazuri clinice, când nu ne vine nimic în minte, logaritmii ne vor ajuta). Prin urmare, acum vom învăța cum să rezolvăm astfel de construcții simple.
Rezolvarea celor mai simple inegalități exponențiale
Să ne uităm la ceva foarte simplu. De exemplu, aici este:
\[((2)^(x)) \gt 4\]
Evident, numărul din dreapta poate fi rescris ca o putere a doi: $4=((2)^(2))$. Astfel, inegalitatea originală este rescrisă într-o formă foarte convenabilă:
\[((2)^(x)) \gt ((2)^(2))\]
Iar acum mâinile sunt mâncărime să „trisească” zeii, stând în bazele gradelor, pentru a obține răspunsul $x \gt 2$. Dar înainte de a tăia ceva, să ne amintim puterile a doi:
\[((2)^(1))=2;\quad ((2)^(2))=4;\quad ((2)^(3))=8;\quad ((2)^( 4))=16;...\]
După cum puteți vedea, cu cât este mai mare numărul din exponent, cu atât este mai mare numărul de ieșire. — Mulțumesc, Cap! va exclama unul dintre elevi. Se întâmplă altfel? Din păcate, se întâmplă. De exemplu:
\[((\left(\frac(1)(2) \right))^(1))=\frac(1)(2);\quad ((\left(\frac(1)(2) \ dreapta))^(2))=\frac(1)(4);\quad ((\left(\frac(1)(2) \right))^(3))=\frac(1)(8 );...\]
Și aici totul este logic: cu cât gradul este mai mare, cu atât numărul 0,5 este înmulțit cu el însuși (adică se împarte la jumătate). Astfel, succesiunea de numere rezultată scade, iar diferența dintre prima și a doua secvență este doar în bază:
- Dacă baza gradului $a \gt 1$, atunci pe măsură ce exponentul $n$ crește, va crește și numărul $((a)^(n))$;
- În schimb, dacă $0 \lt a \lt 1$, atunci pe măsură ce exponentul $n$ crește, numărul $((a)^(n))$ va scădea.
Rezumând aceste fapte, obținem cea mai importantă afirmație, pe care se bazează întreaga soluție a inegalităților exponențiale:
Dacă $a \gt 1$, atunci inegalitatea $((a)^(x)) \gt ((a)^(n))$ este echivalentă cu inegalitatea $x \gt n$. Dacă $0 \lt a \lt 1$, atunci inegalitatea $((a)^(x)) \gt ((a)^(n))$ este echivalentă cu inegalitatea $x \lt n$.
Cu alte cuvinte, dacă baza este mai mare decât unu, o puteți elimina pur și simplu - semnul inegalității nu se va schimba. Și dacă baza este mai mică de unu, atunci poate fi, de asemenea, eliminată, dar și semnul inegalității va trebui schimbat.
Rețineți că nu am luat în considerare opțiunile $a=1$ și $a\le 0$. Pentru că în aceste cazuri există incertitudine. Să presupunem cum se rezolvă o inegalitate de forma $((1)^(x)) \gt 3$? Un unu oricărei puteri va da din nou unul - nu vom primi niciodată un trei sau mai mult. Acestea. nu exista solutii.
Cu baze negative, este și mai interesant. Luați în considerare, de exemplu, următoarea inegalitate:
\[((\left(-2 \right))^(x)) \gt 4\]
La prima vedere, totul este simplu:
Corect? Dar nu! Este suficient să înlocuiți câteva numere pare și câteva impare în loc de $x$ pentru a vă asigura că soluția este greșită. Aruncă o privire:
\[\begin(align) & x=4\Rightarrow ((\left(-2 \right))^(4))=16 \gt 4; \\ & x=5\Rightarrow ((\left(-2 \right))^(5))=-32 \lt 4; \\ & x=6\Rightarrow ((\left(-2 \right))^(6))=64 \gt 4; \\ & x=7\Rightarrow ((\left(-2 \right))^(7))=-128 \lt 4. \\\end(align)\]
După cum puteți vedea, semnele se alternează. Dar există încă grade fracționale și alte staniu. Cum, de exemplu, ați comanda să numărați $((\left(-2 \right))^(\sqrt(7)))$ (minus doi ridicați la rădăcina lui șapte)? În nici un caz!
Prin urmare, pentru certitudine, presupunem că în toate inegalitățile exponențiale (și ecuațiile, de altfel, de asemenea) $1\ne a \gt 0$. Și apoi totul este rezolvat foarte simplu:
\[((a)^(x)) \gt ((a)^(n))\Rightarrow \left[ \begin(align) & x \gt n\quad \left(a \gt 1 \right), \\ & x \lt n\quad \left(0 \lt a \lt 1 \right). \\\end(aliniere) \dreapta.\]
În general, amintiți-vă încă o dată regula principală: dacă baza din ecuația exponențială este mai mare decât unu, o puteți elimina pur și simplu; iar dacă baza este mai mică de unu, poate fi, de asemenea, eliminată, dar acest lucru va schimba semnul inegalității.
Exemple de soluții
Deci, luați în considerare câteva inegalități exponențiale simple:
\[\begin(align) & ((2)^(x-1))\le \frac(1)(\sqrt(2)); \\ & ((0,1)^(1-x)) \lt 0,01; \\ & ((2)^(((x)^(2))-7x+14)) \lt 16; \\ & ((0,2)^(1+((x)^(2))))\ge \frac(1)(25). \\\end(align)\]
Sarcina principală este aceeași în toate cazurile: reducerea inegalităților la cea mai simplă formă $((a)^(x)) \gt ((a)^(n))$. Aceasta este ceea ce vom face acum cu fiecare inegalitate și, în același timp, vom repeta proprietățile puterilor și funcția exponențială. Deci să mergem!
\[((2)^(x-1))\le \frac(1)(\sqrt(2))\]
Ce se poate face aici? Ei bine, în stânga avem deja o expresie demonstrativă - nimic nu trebuie schimbat. Dar în dreapta este un fel de porcărie: o fracție și chiar o rădăcină în numitor!
Cu toate acestea, amintiți-vă regulile de lucru cu fracții și puteri:
\[\begin(align) & \frac(1)(((a)^(n)))=((a)^(-n)); \\ & \sqrt[k](a)=((a)^(\frac(1)(k))). \\\end(align)\]
Ce înseamnă? În primul rând, putem scăpa cu ușurință de fracție transformând-o într-un exponent negativ. Și în al doilea rând, deoarece numitorul este rădăcina, ar fi bine să-l transformăm într-un grad - de data aceasta cu un exponent fracționar.
Să aplicăm secvențial aceste acțiuni în partea dreaptă a inegalității și să vedem ce se întâmplă:
\[\frac(1)(\sqrt(2))=((\left(\sqrt(2) \right))^(-1))=((\left(((2)^(\frac() 1)(3))) \right))^(-1))=((2)^(\frac(1)(3)\cdot \left(-1 \right)))=((2)^ (-\frac(1)(3)))\]
Nu uitați că atunci când ridicați un grad la o putere, se adaugă exponenții acestor grade. Și, în general, atunci când lucrați cu ecuații și inegalități exponențiale, este absolut necesar să cunoașteți cel puțin cele mai simple reguli pentru lucrul cu puteri:
\[\begin(align) & ((a)^(x))\cdot ((a)^(y))=((a)^(x+y)); \\ & \frac(((a)^(x)))(((a)^(y)))=((a)^(x-y)); \\ & ((\left(((a)^(x)) \right))^(y))=((a)^(x\cdot y)). \\\end(align)\]
De fapt, tocmai am aplicat ultima regulă. Prin urmare, inegalitatea noastră originală va fi rescrisă după cum urmează:
\[((2)^(x-1))\le \frac(1)(\sqrt(2))\Rightarrow ((2)^(x-1))\le ((2)^(-\ frac(1)(3)))\]
Acum scăpăm de zeul de la bază. Deoarece 2 > 1, semnul inegalității rămâne același:
\[\begin(align) & x-1\le -\frac(1)(3)\Rightarrow x\le 1-\frac(1)(3)=\frac(2)(3); \\ & x\in \left(-\infty ;\frac(2)(3) \right]. \\\end(align)\]
Asta e toata solutia! Principala dificultate nu este deloc în funcția exponențială, ci în transformarea competentă a expresiei originale: trebuie să o aduceți cu atenție și cât mai repede posibil la forma sa cea mai simplă.
Luați în considerare a doua inegalitate:
\[((0,1)^(1-x)) \lt 0,01\]
Asa si asa. Aici așteptăm fracțiile zecimale. După cum am spus de multe ori, în orice expresii cu puteri, ar trebui să scapi de fracțiile zecimale - adesea aceasta este singura modalitate de a vedea o soluție rapidă și ușoară. Iată de ce vom scăpa:
\[\begin(align) & 0,1=\frac(1)(10);\quad 0,01=\frac(1)(100)=((\left(\frac(1)(10) \ dreapta))^(2)); \\ & ((0,1)^(1-x)) \lt 0,01\Rightarrow ((\left(\frac(1)(10) \right))^(1-x)) \lt ( (\left(\frac(1)(10) \right))^(2)). \\\end(align)\]
În fața noastră este din nou cea mai simplă inegalitate, și chiar și cu baza 1/10, i.e. mai putin de unul. Ei bine, eliminăm bazele, schimbând simultan semnul de la „mai puțin” la „mai mare”, și obținem:
\[\begin(align) & 1-x \gt 2; \\ & -x \gt 2-1; \\ & -x \gt 1; \\& x \lt -1. \\\end(align)\]
Am primit răspunsul final: $x\in \left(-\infty ;-1 \right)$. Vă rugăm să rețineți că răspunsul este exact mulțimea și în niciun caz nu este construcția formei $x \lt -1$. Pentru că formal o astfel de construcție nu este deloc o mulțime, ci o inegalitate față de variabila $x$. Da, este foarte simplu, dar nu este răspunsul!
Notă importantă. Această inegalitate ar putea fi rezolvată într-un alt mod - prin reducerea ambelor părți la o putere cu o bază mai mare de unu. Aruncă o privire:
\[\frac(1)(10)=((10)^(-1))\Rightarrow ((\left(((10)^(-1)) \right))^(1-x)) \ lt ((\left(((10)^(-1)) \right))^(2))\Rightarrow ((10)^(-1\cdot \left(1-x \right))) \lt ((10)^(-1\cdot 2))\]
După o astfel de transformare, obținem din nou o inegalitate exponențială, dar cu o bază de 10 > 1. Și asta înseamnă că puteți tăia pur și simplu zece - semnul inegalității nu se va schimba. Primim:
\[\begin(align) & -1\cdot \left(1-x \right) \lt -1\cdot 2; \\ & x-1 \lt-2; \\ & x \lt -2+1=-1; \\ & x \lt -1. \\\end(align)\]
După cum puteți vedea, răspunsul este exact același. În același timp, ne-am salvat de nevoia de a schimba semnul și, în general, ne-am amintit câteva reguli de acolo. :)
\[((2)^(((x)^(2))-7x+14)) \lt 16\]
Totuși, nu lăsa asta să te sperie. Indiferent ce se află în indicatori, tehnologia de rezolvare a inegalității în sine rămâne aceeași. Prin urmare, observăm mai întâi că 16 = 2 4 . Să rescriem inegalitatea inițială ținând cont de acest fapt:
\[\begin(align) & ((2)^(((x)^(2))-7x+14)) \lt ((2)^(4)); \\ & ((x)^(2))-7x+14 \lt 4; \\ & ((x)^(2))-7x+10 \lt 0. \\\end(align)\]
Ura! Avem inegalitatea pătrată obișnuită! Semnul nu s-a schimbat nicăieri, deoarece baza este un doi - un număr mai mare decât unu.
Funcția zerouri pe linia numerică
Aranjam semnele functiei $f\left(x \right)=((x)^(2))-7x+10$ - evident, graficul acesteia va fi o parabolă cu ramuri în sus, deci vor fi „plusuri” ” pe laterale. Ne interesează regiunea în care funcția este mai mică decât zero, adică. $x\in \left(2;5 \right)$ este răspunsul la problema inițială.
În cele din urmă, luați în considerare o altă inegalitate:
\[((0,2)^(1+((x)^(2))))\ge \frac(1)(25)\]
Din nou vedem o funcție exponențială cu o fracție zecimală în bază. Să transformăm această fracție într-o fracție comună:
\[\begin(align) & 0,2=\frac(2)(10)=\frac(1)(5)=((5)^(-1))\Rightarrow \\ & \Rightarrow ((0 ,2)^(1+((x)^(2))))=((\left(((5)^(-1)) \right))^(1+((x)^(2) )))=((5)^(-1\cdot \left(1+((x)^(2)) \right)))\end(align)\]
În acest caz, am profitat de observația făcută mai devreme - am redus baza la numărul 5\u003e 1 pentru a simplifica decizia noastră ulterioară. Să facem același lucru cu partea dreaptă:
\[\frac(1)(25)=((\left(\frac(1)(5) \right))^(2))=((\left(((5)^(-1)) \ dreapta))^(2))=((5)^(-1\cdot 2))=((5)^(-2))\]
Să rescriem inegalitatea inițială, ținând cont de ambele transformări:
\[(((0,2)^(1+((x)^(2))))\ge \frac(1)(25)\Rightarrow ((5)^(-1\cdot \left(1+) ((x)^(2)) \dreapta)))\ge ((5)^(-2))\]
Bazele de pe ambele părți sunt aceleași și mai mari decât una. Nu există alți termeni la dreapta și la stânga, așa că pur și simplu „tașăm” cei cinci și obținem o expresie foarte simplă:
\[\begin(align) & -1\cdot \left(1+((x)^(2)) \right)\ge -2; \\ & -1-((x)^(2))\ge -2; \\ & -((x)^(2))\ge -2+1; \\ & -((x)^(2))\ge -1;\quad \left| \cdot \left(-1 \right) \right. \\ & ((x)^(2))\le 1. \\\end(align)\]
Aici trebuie să fii atent. Mulți studenți le place să ia pur și simplu rădăcina pătrată a ambelor părți ale inegalității și să scrie ceva de genul $x\le 1\Rightarrow x\in \left(-\infty ;-1 \right]$. Nu ar trebui să faceți niciodată acest lucru, deoarece rădăcina pătratului exact este modulul și în niciun caz variabila inițială:
\[\sqrt(((x)^(2)))=\left| x\dreapta|\]
Cu toate acestea, lucrul cu module nu este cea mai plăcută experiență, nu? Deci nu vom lucra. În schimb, pur și simplu mutăm toți termenii la stânga și rezolvăm inegalitatea obișnuită folosind metoda intervalului:
$\begin(align) & ((x)^(2))-1\le 0; \\ & \left(x-1 \right)\left(x+1 \right)\le 0 \\ & ((x)_(1))=1;\quad ((x)_(2)) =-1; \\\end(align)$
Din nou, notăm punctele obținute pe linia numerică și ne uităm la semnele:
 Vă rugăm să rețineți: punctele sunt umbrite.
Vă rugăm să rețineți: punctele sunt umbrite. Deoarece rezolvăm o inegalitate nestrictă, toate punctele din grafic sunt umbrite. Prin urmare, răspunsul va fi: $x\in \left[ -1;1 \right]$ nu este un interval, ci un segment.
În general, aș dori să observ că nu este nimic complicat în inegalitățile exponențiale. Semnificația tuturor transformărilor pe care le-am efectuat astăzi se rezumă la un simplu algoritm:
- Găsiți baza la care vom reduce toate gradele;
- Efectuați cu atenție transformări pentru a obține o inegalitate de forma $((a)^(x)) \gt ((a)^(n))$. Desigur, în loc de variabilele $x$ și $n$, pot fi mult mai multe funcții complexe, dar sensul acestui lucru nu se va schimba;
- Tăiați bazele gradelor. În acest caz, semnul de inegalitate se poate schimba dacă baza $a \lt 1$.
De fapt, acesta este un algoritm universal pentru rezolvarea tuturor acestor inegalități. Și tot ceea ce vi se va spune pe această temă este doar trucuri și trucuri specifice pentru a simplifica și accelera transformarea. Iată unul dintre acele trucuri despre care vom vorbi acum. :)
metoda de raționalizare
Luați în considerare un alt lot de inegalități:
\[\begin(align) & ((\text( )\!\!\pi\!\!\text( ))^(x+7)) \gt ((\text( )\!\!\pi \!\!\text( ))^(((x)^(2))-3x+2)); \\ & ((\left(2\sqrt(3)-3 \right))^(((x)^(2))-2x)) \lt 1; \\ & ((\left(\frac(1)(3) \right)))^(((x)^(2))+2x)) \gt ((\left(\frac(1)(9)) \dreapta))^(16-x)); \\ & ((\left(3-2\sqrt(2) \right))^(3x-((x)^(2)))) \lt 1. \\\end(align)\]
Ei bine, ce este atât de special la ei? De asemenea, sunt ușoare. Deși, oprește-te! Este pi ridicat la putere? Ce fel de prostii?
Și cum să ridici numărul $2\sqrt(3)-3$ la o putere? Sau $3-2\sqrt(2)$? Compilatorii problemelor au băut, evident, prea mult „păducel” înainte de a se așeza la muncă. :)
De fapt, nu este nimic în neregulă cu aceste sarcini. Permiteți-mi să vă reamintesc: o funcție exponențială este o expresie de forma $((a)^(x))$, unde baza $a$ este orice număr pozitiv, cu excepția unuia. Numărul π este pozitiv - știm deja acest lucru. Numerele $2\sqrt(3)-3$ și $3-2\sqrt(2)$ sunt de asemenea pozitive - acest lucru este ușor de văzut dacă le comparăm cu zero.
Se pare că toate aceste inegalități „terifiante” nu sunt diferite de cele simple discutate mai sus? Și ei o fac la fel? Da, absolut corect. Cu toate acestea, folosind exemplul lor, aș dori să iau în considerare un truc care economisește mult timp pentru munca independentă și examene. Vom vorbi despre metoda raționalizării. Deci atentie:
Orice inegalitate exponențială de forma $((a)^(x)) \gt ((a)^(n))$ este echivalentă cu inegalitatea $\left(x-n \right)\cdot \left(a-1 \ dreapta) \gt 0 $.
Asta e toată metoda. :) Te-ai gândit că va exista un fel de următor joc? Nimic de genul asta! Dar acest simplu fapt, scris literalmente într-o singură linie, ne va simplifica foarte mult munca. Aruncă o privire:
\[\begin(matrix) ((\text( )\!\!\pi\!\!\text( ))^(x+7)) \gt ((\text( )\!\!\pi\ !\!\text( ))^(((x)^(2))-3x+2)) \\ \Downarrow \\ \left(x+7-\left(((x)^(2)) -3x+2 \right) \right)\cdot \left(\text( )\!\!\pi\!\!\text( )-1 \right) \gt 0 \\\end(matrix)\]
Aici nu mai există funcții exponențiale! Și nu trebuie să vă amintiți dacă semnul se schimbă sau nu. Dar apare o nouă problemă: ce să faci cu multiplicatorul nenorocit \[\left(\text( )\!\!\pi\!\!\text( )-1 \right)\]? Nu știm care este valoarea exactă a lui pi. Cu toate acestea, căpitanul pare să sugereze ceea ce este evident:
\[\text( )\!\!\pi\!\!\text( )\approx 3,14... \gt 3\Rightarrow \text( )\!\!\pi\!\!\text( )-1 \gt 3-1=2\]
În general, valoarea exactă a lui π nu ne deranjează prea mult - este important doar pentru noi să înțelegem că în orice caz $\text( )\!\!\pi\!\!\text( )-1 \gt 2 $, t .e. este o constantă pozitivă și putem împărți ambele părți ale inegalității cu aceasta:
\[\begin(align) & \left(x+7-\left(((x)^(2))-3x+2 \right) \right)\cdot \left(\text( )\!\! \pi\!\!\text( )-1 \right) \gt 0 \\ & x+7-\left(((x)^(2))-3x+2 \right) \gt 0; \\ & x+7-((x)^(2))+3x-2 \gt 0; \\ & -((x)^(2))+4x+5 \gt 0;\quad \left| \cdot \left(-1 \right) \right. \\ & ((x)^(2))-4x-5 \lt 0; \\ & \left(x-5 \right)\left(x+1 \right) \lt 0. \\\end(align)\]
După cum puteți vedea, la un moment dat, a trebuit să împărțim cu minus unu, iar semnul inegalității s-a schimbat. La final, am extins trinomul pătrat conform teoremei Vieta - este evident că rădăcinile sunt egale cu $((x)_(1))=5$ și $((x)_(2))=- 1 $. Apoi totul este rezolvat prin metoda clasică a intervalelor:
 Rezolvăm inegalitatea prin metoda intervalelor
Rezolvăm inegalitatea prin metoda intervalelor Toate punctele sunt perforate deoarece inegalitatea originală este strictă. Ne interesează zona cu valori negative, deci răspunsul este $x\in \left(-1;5 \right)$. asta e solutia. :)
Să trecem la următoarea sarcină:
\[((\left(2\sqrt(3)-3 \right))^(((x)^(2))-2x)) \lt 1\]
Totul este simplu aici, pentru că în dreapta este o unitate. Și ne amintim că o unitate este orice număr ridicat la puterea lui zero. Chiar dacă acest număr este o expresie irațională, stând la baza din stânga:
\[\begin(align) & ((\left(2\sqrt(3)-3 \right))^(((x)^(2))-2x)) \lt 1=((\left(2) \sqrt(3)-3\right))^(0)); \\ & ((\left(2\sqrt(3)-3 \right))^(((x)^(2))-2x)) \lt ((\left(2\sqrt(3)-3) \dreapta))^(0)); \\\end(align)\]
Deci hai sa rationalizam:
\[\begin(align) & \left(((x)^(2))-2x-0 \right)\cdot \left(2\sqrt(3)-3-1 \right) \lt 0; \\ & \left(((x)^(2))-2x-0 \right)\cdot \left(2\sqrt(3)-4 \right) \lt 0; \\ & \left(((x)^(2))-2x-0 \right)\cdot 2\left(\sqrt(3)-2 \right) \lt 0. \\\end(align)\ ]
Rămâne doar să ne ocupăm de semne. Multiplicatorul $2\left(\sqrt(3)-2 \right)$ nu conține variabila $x$ - este doar o constantă și trebuie să aflăm semnul acesteia. Pentru a face acest lucru, rețineți următoarele:
\[\begin(matrix) \sqrt(3) \lt \sqrt(4)=2 \\ \Downarrow \\ 2\left(\sqrt(3)-2 \right) \lt 2\cdot \left(2 -2 \right)=0 \\\end(matrice)\]
Se pare că al doilea factor nu este doar o constantă, ci o constantă negativă! Și la împărțirea cu acesta, semnul inegalității originale se va schimba în opus:
\[\begin(align) & \left(((x)^(2))-2x-0 \right)\cdot 2\left(\sqrt(3)-2 \right) \lt 0; \\ & ((x)^(2))-2x-0 \gt 0; \\ & x\left(x-2 \right) \gt 0. \\\end(align)\]
Acum totul devine destul de evident. Rădăcinile trinomului pătrat din dreapta sunt $((x)_(1))=0$ și $((x)_(2))=2$. Le marchem pe linia numerică și ne uităm la semnele funcției $f\left(x \right)=x\left(x-2 \right)$:
 Cazul când ne interesează intervalele laterale
Cazul când ne interesează intervalele laterale Ne interesează intervalele marcate cu semnul plus. Rămâne doar să scrieți răspunsul:
Să trecem la următorul exemplu:
\[((\left(\frac(1)(3) \right)))^(((x)^(2))+2x)) \gt ((\left(\frac(1)(9) \ dreapta))^(16-x))\]
Ei bine, totul este destul de evident aici: bazele sunt puteri de același număr. Prin urmare, voi scrie totul pe scurt:
\[\begin(matrix) \frac(1)(3)=((3)^(-1));\quad \frac(1)(9)=\frac(1)(((3)^( 2)))=((3)^(-2)) \\ \În jos \\ ((\left(((3)^(-1)) \right))^(((x)^(2) )+2x)) \gt ((\left(((3)^(-2)) \right))^(16-x)) \\\end(matrice)\]
\[\begin(align) & ((3)^(-1\cdot \left(((x)^(2))+2x \right))) \gt ((3)^(-2\cdot \ stânga(16-x\dreapta))); \\ & ((3)^(-((x)^(2))-2x)) \gt ((3)^(-32+2x)); \\ & \left(-((x)^(2))-2x-\left(-32+2x \right) \right)\cdot \left(3-1 \right) \gt 0; \\ & -((x)^(2))-2x+32-2x \gt 0; \\ & -((x)^(2))-4x+32 \gt 0;\quad \left| \cdot \left(-1 \right) \right. \\ & ((x)^(2))+4x-32 \lt 0; \\ & \left(x+8 \right)\left(x-4 \right) \lt 0. \\\end(align)\]
După cum puteți vedea, în procesul transformărilor, a trebuit să înmulțim cu un număr negativ, așa că semnul inegalității s-a schimbat. La final, am aplicat din nou teorema lui Vieta pentru a factoriza un trinom pătrat. Ca urmare, răspunsul va fi următorul: $x\in \left(-8;4 \right)$ - cei care doresc pot verifica acest lucru prin trasarea unei linii numerice, marcarea punctelor și numărarea semnelor. Între timp, vom trece la ultima inegalitate din „setul” nostru:
\[((\left(3-2\sqrt(2) \right))^(3x-((x)^(2)))) \lt 1\]
După cum puteți vedea, baza este din nou un număr irațional, iar unitatea este din nou în dreapta. Prin urmare, rescriem inegalitatea noastră exponențială după cum urmează:
\[((\left(3-2\sqrt(2) \right))^(3x-((x)^(2)))) \lt ((\left(3-2\sqrt(2)) \ dreapta))^(0))\]
Să raționalizăm:
\[\begin(align) & \left(3x-((x)^(2))-0 \right)\cdot \left(3-2\sqrt(2)-1 \right) \lt 0; \\ & \left(3x-((x)^(2))-0 \right)\cdot \left(2-2\sqrt(2) \right) \lt 0; \\ & \left(3x-((x)^(2))-0 \right)\cdot 2\left(1-\sqrt(2) \right) \lt 0. \\\end(align)\ ]
Cu toate acestea, este destul de evident că $1-\sqrt(2) \lt 0$, deoarece $\sqrt(2)\aproximativ 1,4... \gt 1$. Prin urmare, al doilea factor este din nou o constantă negativă, prin care ambele părți ale inegalității pot fi împărțite:
\[\begin(matrix) \left(3x-((x)^(2))-0 \right)\cdot 2\left(1-\sqrt(2) \right) \lt 0 \\ \Downarrow \ \\end(matrice)\]
\[\begin(align) & 3x-((x)^(2))-0 \gt 0; \\ & 3x-((x)^(2)) \gt 0;\quad \left| \cdot \left(-1 \right) \right. \\ & ((x)^(2))-3x \lt 0; \\ & x\left(x-3 \right) \lt 0. \\\end(align)\]
Schimbați-vă la altă bază
O problemă separată în rezolvarea inegalităților exponențiale este căutarea bazei „corecte”. Din păcate, la prima vedere asupra sarcinii, este departe de a fi întotdeauna evident ce să ia ca bază și ce să facă ca gradul acestei baze.
Dar nu vă faceți griji: aici nu există magie și tehnologii „secrete”. În matematică, orice abilitate care nu poate fi algoritmizată poate fi dezvoltată cu ușurință prin practică. Dar pentru aceasta va trebui să rezolvați probleme de diferite niveluri de complexitate. De exemplu, acestea sunt:
\[\begin(align) & ((2)^(\frac(x)(2))) \lt ((4)^(\frac(4)(x))); \\ & ((\left(\frac(1)(3) \right))^(\frac(3)(x)))\ge ((3)^(2+x)); \\ & ((\left(0,16 \right))^(1+2x))\cdot ((\left(6,25 \right))^(x))\ge 1; \\ & ((\left(\frac(27)(\sqrt(3)) \right))^(-x)) \lt ((9)^(4-2x))\cdot 81. \\\ sfârşitul (alinierea)\]
Complicat? Infricosator? Da, e mai ușor decât un pui pe asfalt! Sa incercam. Prima inegalitate:
\[((2)^(\frac(x)(2))) \lt ((4)^(\frac(4)(x)))\]
Ei bine, cred că totul este clar aici:
Rescriem inegalitatea originală, reducând totul la baza „două”:
\[((2)^(\frac(x)(2))) \lt ((2)^(\frac(8)(x)))\Rightarrow \left(\frac(x)(2)- \frac(8)(x) \right)\cdot \left(2-1 \right) \lt 0\]
Da, da, ați înțeles bine: tocmai am aplicat metoda de raționalizare descrisă mai sus. Acum trebuie să lucrăm cu atenție: avem o inegalitate fracționară-rațională (aceasta este una care are o variabilă la numitor), așa că înainte de a echivala ceva cu zero, trebuie să aduceți totul la numitor comunși scăpați de multiplicatorul constant.
\[\begin(align) & \left(\frac(x)(2)-\frac(8)(x) \right)\cdot \left(2-1 \right) \lt 0; \\ & \left(\frac(((x)^(2))-16)(2x) \right)\cdot 1 \lt 0; \\ & \frac(((x)^(2))-16)(2x) \lt 0. \\\end(align)\]
Acum folosim metoda intervalului standard. Zerourile numeratorului: $x=\pm 4$. Numitorul ajunge la zero numai atunci când $x=0$. În total, sunt trei puncte care ar trebui marcate pe linia numerică (toate punctele sunt scoase, deoarece semnul inegalității este strict). Primim:
 Caz mai complicat: trei rădăcini
Caz mai complicat: trei rădăcini După cum ați putea ghici, hașura marchează intervalele la care expresia din stânga ia valori negative. Prin urmare, două intervale vor intra în răspunsul final simultan:
Capetele intervalelor nu sunt incluse în răspuns deoarece inegalitatea inițială a fost strictă. Nu este necesară nicio validare suplimentară a acestui răspuns. În acest sens, inegalitățile exponențiale sunt mult mai simple decât cele logaritmice: fără DPV, fără restricții etc.
Să trecem la următoarea sarcină:
\[((\left(\frac(1)(3) \right))^(\frac(3)(x)))\ge ((3)^(2+x))\]
Nici aici nu există probleme, deoarece știm deja că $\frac(1)(3)=((3)^(-1))$, deci întreaga inegalitate poate fi rescrisă astfel:
\[\begin(align) & ((\left(((3)^(-1)) \right))^(\frac(3)(x)))\ge ((3)^(2+x ))\Rightarrow ((3)^(-\frac(3)(x)))\ge ((3)^(2+x)); \\ & \left(-\frac(3)(x)-\left(2+x \right) \right)\cdot \left(3-1 \right)\ge 0; \\ & \left(-\frac(3)(x)-2-x \right)\cdot 2\ge 0;\quad \left| :\stânga(-2\dreapta)\dreapta. \\ & \frac(3)(x)+2+x\le 0; \\ & \frac(((x)^(2))+2x+3)(x)\le 0. \\\end(align)\]
Vă rugăm să rețineți: în a treia linie, am decis să nu pierd timpul cu fleacuri și să împart imediat totul la (−2). Minul a intrat în prima paranteză (acum sunt plusuri peste tot), iar deuce a fost redus cu un multiplicator constant. Este exact ceea ce ar trebui să faceți atunci când faceți calcule reale pe independent și munca de control- nu este nevoie să pictezi direct fiecare acțiune și transformare.
În continuare, intră în joc metoda familiară a intervalelor. Zerurile numărătorului: dar nu există. Pentru că discriminantul va fi negativ. La rândul său, numitorul este setat la zero numai atunci când $x=0$ - la fel ca data trecută. Ei bine, este clar că fracția va lua valori pozitive la dreapta lui $x=0$ și negative la stânga. Deoarece ne interesează doar valorile negative, răspunsul final este $x\in \left(-\infty ;0 \right)$.
\[((\left(0,16 \right))^(1+2x))\cdot ((\left(6,25 \right))^(x))\ge 1\]
Și ce ar trebui făcut cu fracțiile zecimale în inegalități exponențiale? Așa este: scapă de ele transformându-le în altele obișnuite. Aici traducem:
\[\begin(align) & 0,16=\frac(16)(100)=\frac(4)(25)\Rightarrow ((\left(0,16 \right))^(1+2x)) =((\left(\frac(4)(25) \right))^(1+2x)); \\ & 6,25=\frac(625)(100)=\frac(25)(4)\Rightarrow ((\left(6,25 \right))^(x))=((\left(\ frac(25)(4) \right))^(x)). \\\end(align)\]
Ei bine, ce am obținut în bazele funcțiilor exponențiale? Și avem două numere reciproc reciproce:
\[\frac(25)(4)=((\left(\frac(4)(25) \right))^(-1))\Rightarrow ((\left(\frac(25)(4) \ dreapta))^(x))=((\left(((\left(\frac(4)(25) \right))^(-1)) \right))^(x))=((\ stânga(\frac(4)(25) \dreapta))^(-x))\]
Astfel, inegalitatea originală poate fi rescrisă după cum urmează:
\[\begin(align) & ((\left(\frac(4)(25) \right))^(1+2x))\cdot ((\left(\frac(4)(25) \right) )^(-x))\ge 1; \\ & ((\left(\frac(4)(25) \right))^(1+2x+\left(-x \right)))\ge ((\left(\frac(4)(25) \dreapta))^(0)); \\ & ((\left(\frac(4)(25) \right))^(x+1))\ge ((\left(\frac(4)(25) \right))^(0) ). \\\end(align)\]
Desigur, la înmulțirea puterilor cu aceeași bază, indicatorii lor se adună, ceea ce s-a întâmplat în a doua linie. In plus, am reprezentat unitatea in dreapta, tot ca putere in baza 4/25. Rămâne doar să raționalizezi:
\[((\left(\frac(4)(25) \right))^(x+1))\ge ((\left(\frac(4)(25) \right))^(0)) \Rightarrow \left(x+1-0 \right)\cdot \left(\frac(4)(25)-1 \right)\ge 0\]
Rețineți că $\frac(4)(25)-1=\frac(4-25)(25) \lt 0$, adică. cel de-al doilea factor este o constantă negativă, iar atunci când este împărțit la acesta, semnul inegalității se va schimba:
\[\begin(align) & x+1-0\le 0\Rightarrow x\le -1; \\ & x\in \left(-\infty ;-1 \right]. \\\end(align)\]
În cele din urmă, ultima inegalitate din „mulțimea” actuală:
\[((\left(\frac(27)(\sqrt(3)) \right))^(-x)) \lt ((9)^(4-2x))\cdot 81\]
În principiu, ideea unei soluții aici este de asemenea clară: toate funcțiile exponențiale care compun inegalitatea trebuie reduse la baza „3”. Dar pentru asta trebuie să te joci puțin cu rădăcini și grade:
\[\begin(align) & \frac(27)(\sqrt(3))=\frac((((3)^(3)))(((3)^(\frac(1)(3)) ))=((3)^(3-\frac(1)(3)))=((3)^(\frac(8)(3))); \\ & 9=((3)^(2));\quad 81=((3)^(4)). \\\end(align)\]
Având în vedere aceste fapte, inegalitatea inițială poate fi rescrisă după cum urmează:
\[\begin(align) & ((\left(((3)^(\frac(8)(3))) \right))^(-x)) \lt ((\left(((3)) ^(2)) \right))^(4-2x))\cdot ((3)^(4)); \\ & ((3)^(-\frac(8x)(3))) \lt ((3)^(8-4x))\cdot ((3)^(4)); \\ & ((3)^(-\frac(8x)(3))) \lt ((3)^(8-4x+4)); \\ & ((3)^(-\frac(8x)(3))) \lt ((3)^(4-4x)). \\\end(align)\]
Atenție la rândul 2 și 3 de calcule: înainte de a face ceva cu inegalitatea, asigurați-vă că îl aduceți la forma despre care am vorbit încă de la începutul lecției: $((a)^(x)) \lt ( (a)^(n))$. Atâta timp cât aveți multiplicatori stânga sau dreapta stânga, constante suplimentare etc., nu poate fi efectuată nicio raționalizare și „radiere” a terenurilor! Nenumărate sarcini au fost greșite din cauza unei neînțelegeri a acestui simplu fapt. Eu însumi observ constant această problemă cu studenții mei când abia începem să analizăm inegalitățile exponențiale și logaritmice.
Dar să revenim la sarcina noastră. Să încercăm de data asta să facem fără raționalizare. Ne amintim: baza gradului este mai mare decât unu, astfel încât triplele pot fi pur și simplu tăiate - semnul inegalității nu se va schimba. Primim:
\[\begin(align) & -\frac(8x)(3) \lt 4-4x; \\ & 4x-\frac(8x)(3) \lt 4; \\ & \frac(4x)(3) \lt 4; \\ & 4x \lt 12; \\ & x \lt 3. \\\end(align)\]
Asta e tot. Răspuns final: $x\in \left(-\infty ;3 \right)$.
Evidențierea unei expresii stabile și înlocuirea unei variabile
În concluzie, îmi propun să rezolvăm încă patru inegalități exponențiale, care sunt deja destul de dificile pentru elevii nepregătiți. Pentru a le face față, trebuie să vă amintiți regulile de lucru cu grade. În special, scoaterea din paranteze a factorilor comuni.
Dar cel mai important lucru este să înveți să înțelegi: ce anume poate fi pus în paranteze. O astfel de expresie se numește stabilă - poate fi notată printr-o nouă variabilă și astfel scăpați de funcția exponențială. Deci, să ne uităm la sarcini:
\[\begin(align) & ((5)^(x+2))+((5)^(x+1))\ge 6; \\ & ((3)^(x))+((3)^(x+2))\ge 90; \\ & ((25)^(x+1,5))-((5)^(2x+2)) \gt 2500; \\ & ((\left(0,5 \right))^(-4x-8))-((16)^(x+1,5)) \gt 768. \\\end(align)\]
Să începem cu prima linie. Să scriem separat această inegalitate:
\[((5)^(x+2))+((5)^(x+1))\ge 6\]
Rețineți că $((5)^(x+2))=((5)^(x+1+1))=((5)^(x+1))\cdot 5$, astfel încât partea dreaptă poate fi rescris:
Rețineți că nu există alte funcții exponențiale cu excepția $((5)^(x+1))$ în inegalitate. Și, în general, variabila $x$ nu apare în altă parte, așa că să introducem o nouă variabilă: $((5)^(x+1))=t$. Obținem următoarea construcție:
\[\begin(align) & 5t+t\ge 6; \\ & 6t\ge 6; \\ & t\ge 1. \\\end(align)\]
Revenim la variabila originală ($t=((5)^(x+1))$), și în același timp ne amintim că 1=5 0 . Noi avem:
\[\begin(align) & ((5)^(x+1))\ge ((5)^(0)); \\ &x+1\ge 0; \\ & x\ge -1. \\\end(align)\]
Asta e toata solutia! Răspuns: $x\în \left[ -1;+\infty \right)$. Să trecem la a doua inegalitate:
\[((3)^(x))+((3)^(x+2))\ge 90\]
Totul este la fel aici. Rețineți că $((3)^(x+2))=((3)^(x))\cdot ((3)^(2))=9\cdot ((3)^(x))$ . Apoi partea stângă poate fi rescrisă:
\[\begin(align) & ((3)^(x))+9\cdot ((3)^(x))\ge 90;\quad \left| ((3)^(x))=t \dreapta. \\&t+9t\ge 90; \\ & 10t\ge 90; \\ & t\ge 9\Rightarrow ((3)^(x))\ge 9\Rightarrow ((3)^(x))\ge ((3)^(2)); \\ & x\ge 2\Rightarrow x\in \left[ 2;+\infty \right). \\\end(align)\]
Cam așa trebuie să elaborezi o decizie privind controlul real și munca independentă.
Ei bine, hai să încercăm ceva mai dificil. De exemplu, iată o inegalitate:
\[((25)^(x+1,5))-((5)^(2x+2)) \gt 2500\]
Care este problema aici? În primul rând, bazele funcțiilor exponențiale din stânga sunt diferite: 5 și 25. Cu toate acestea, 25 \u003d 5 2, deci primul termen poate fi transformat:
\[\begin(align) & ((25)^(x+1,5))=((\left((((5)^(2)) \right))^(x+1,5))= ((5)^(2x+3)); \\ & ((5)^(2x+3))=((5)^(2x+2+1))=((5)^(2x+2))\cdot 5. \\\end(align) )\]
După cum puteți vedea, la început am adus totul la aceeași bază, apoi am observat că primul termen este ușor redus la al doilea - este suficient doar să extindeți exponentul. Acum putem introduce în siguranță o nouă variabilă: $((5)^(2x+2))=t$, iar întreaga inegalitate va fi rescrisă astfel:
\[\begin(align) & 5t-t\ge 2500; \\ & 4t\ge 2500; \\ & t\ge 625=((5)^(4)); \\ & ((5)^(2x+2))\ge ((5)^(4)); \\ & 2x+2\ge 4; \\ & 2x\ge 2; \\ & x\ge 1. \\\end(align)\]
Din nou, nicio problemă! Răspuns final: $x\in \left[ 1;+\infty \right)$. Trecând la inegalitatea finală în lecția de astăzi:
\[((\left(0,5 \right))^(-4x-8))-((16)^(x+1,5)) \gt 768\]
Primul lucru de remarcat este, desigur, zecimal la baza gradului I. Este necesar să scăpați de el și, în același timp, să aduceți toate funcțiile exponențiale la aceeași bază - numărul „2”:
\[\begin(align) & 0,5=\frac(1)(2)=((2)^(-1))\Rightarrow ((\left(0,5 \right))^(-4x- 8))=((\left(((2)^(-1)) \right))^(-4x-8))=((2)^(4x+8)); \\ & 16=((2)^(4))\Rightarrow ((16)^(x+1,5))=((\left(((2)^(4)) \right))^( x+1,5))=((2)^(4x+6)); \\ & ((2)^(4x+8))-((2)^(4x+6)) \gt 768. \\\end(align)\]
Grozav, am făcut primul pas - totul a dus la aceeași fundație. Acum trebuie să evidențiem expresia stabilă. Rețineți că $((2)^(4x+8))=((2)^(4x+6+2))=((2)^(4x+6))\cdot 4$. Dacă introducem o nouă variabilă $((2)^(4x+6))=t$, atunci inegalitatea originală poate fi rescrisă după cum urmează:
\[\begin(align) & 4t-t \gt 768; \\ & 3t \gt 768; \\ & t \gt 256=((2)^(8)); \\ & ((2)^(4x+6)) \gt ((2)^(8)); \\ & 4x+6 \gt 8; \\ & 4x \gt 2; \\ & x \gt \frac(1)(2)=0,5. \\\end(align)\]
Desigur, poate apărea întrebarea: cum am aflat că 256 = 2 8? Din păcate, aici trebuie doar să cunoști puterile lui doi (și în același timp puterile lui trei și cinci). Ei bine, sau împărțiți 256 la 2 (puteți împărți, deoarece 256 este un număr par) până când obținem rezultatul. Va arata cam asa:
\[\begin(align) & 256=128\cdot 2= \\ & =64\cdot 2\cdot 2= \\ & =32\cdot 2\cdot 2\cdot 2= \\ & =16\cdot 2 \cdot 2\cdot 2\cdot 2= \\ & =8\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =4\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =((2)^(8)).\end(align )\]
La fel este și cu cele trei (numerele 9, 27, 81 și 243 sunt puterile sale), și cu cele șapte (numerele 49 și 343 ar fi, de asemenea, bine de reținut). Ei bine, cei cinci au și grade „frumoase” pe care trebuie să le știi:
\[\begin(align) & ((5)^(2))=25; \\ & ((5)^(3))=125; \\ & ((5)^(4))=625; \\ & ((5)^(5))=3125. \\\end(align)\]
Desigur, toate aceste numere, dacă se dorește, pot fi restaurate în minte, pur și simplu înmulțindu-le succesiv unele cu altele. Totuși, atunci când trebuie să rezolvi mai multe inegalități exponențiale, iar fiecare următoare este mai dificilă decât cea anterioară, atunci ultimul lucru la care vrei să te gândești este puterile unor numere de acolo. Și în acest sens, aceste probleme sunt mai complexe decât inegalitățile „clasice”, care se rezolvă prin metoda intervalului.
Sper că această lecție te-a ajutat să stăpânești acest subiect. Dacă ceva nu este clar, întrebați în comentarii. Și ne vedem în următoarele tutoriale. :)
Acesta este obligatoriu la rezolvarea unui sistem de ecuaţii exponenţiale? Cu siguranță, transformare acest sistem într-un sistem de ecuații simple.
Exemple.
Rezolvarea sistemelor de ecuații:
Expres la prin X din (2) --a ecuație a sistemului și înlocuiți această valoare în (1) --a ecuație a sistemului.
Rezolvăm ecuația (2)-a a sistemului rezultat:
2 x +2 x +2 =10, aplicați formula: un x + y=un x∙ Ay.
2 x +2 x ∙2 2 \u003d 10, scoatem din paranteze factorul comun 2 x:
2 x (1+2 2)=10 sau 2 x ∙5=10, deci 2 x =2.
2 x \u003d 2 1, de aici x=1. Revenim la sistemul de ecuații.

Răspuns: (1; 2).
Decizie.
Reprezentăm părțile din stânga și din dreapta ale ecuației (1) ca puteri cu bază 2 , iar partea dreaptă a ecuației (2) ca putere zero a numărului 5 .
Dacă două grade cu aceleași baze sunt egale, atunci exponenții acestor grade sunt egali - echivalăm exponenții cu bazele 2 și exponenți cu baze 5 .
Sistemul rezultat ecuatii lineare cu două variabile rezolvăm prin metoda adunării.
Găsim x=2și înlocuiți această valoare cu Xîn a doua ecuație a sistemului.
Găsim la.
Răspuns: (2; 1,5).

Decizie.
Dacă în cele două exemple anterioare am trecut la un sistem mai simplu prin echivalarea exponenților de două grade cu aceleași baze, atunci în al 3-lea exemplu această operație este imposibilă. Este convenabil să rezolvi astfel de sisteme prin introducerea de noi variabile. Vom introduce variabile uși v,și apoi exprimă variabila u prin vși obțineți o ecuație pentru variabilă v.
Rezolvăm (2) -a-a ecuație a sistemului.
v 2 +63v-64=0. Selectăm rădăcinile după teorema Vieta, știind că: v 1 + v 2 =-63; v 1 ∙ v 2 \u003d -64.
Obținem: v 1 \u003d -64, v 2 \u003d 1. Ne întoarcem la sistem, te găsim.

Deoarece valorile funcției exponențiale sunt întotdeauna pozitive, ecuațiile 4 x = -1 și 4y = -64 nu au solutii.
Modalități de rezolvare a sistemelor de ecuații
Pentru început, să ne amintim pe scurt ce metode de rezolvare a sistemelor de ecuații există în general.
Exista patru moduri principale soluții ale sistemelor de ecuații:
Metoda substituției: luați oricare dintre aceste ecuații și exprimați $y$ în termeni de $x$, apoi $y$ este înlocuit în ecuația sistemului, de unde se găsește variabila $x.$ După aceea, putem ușor se calculează variabila $y.$
Metoda adunării: în această metodă, una sau ambele ecuații trebuie înmulțite cu numere astfel încât, atunci când ambele sunt adunate împreună, una dintre variabile „dispare”.
Metoda grafică: ambele ecuații ale sistemului sunt afișate pe planul de coordonate și se găsește punctul de intersecție a acestora.
Metoda introducerii de noi variabile: în această metodă, facem înlocuirea unor expresii pentru a simplifica sistemul, apoi aplicăm una dintre metodele de mai sus.
Sisteme de ecuații exponențiale
Definiția 1
Sistemele de ecuații formate din ecuații exponențiale se numesc sistem de ecuații exponențiale.
Vom lua în considerare soluția sistemelor de ecuații exponențiale folosind exemple.
Exemplul 1
Rezolvați un sistem de ecuații
Poza 1.
Decizie.
Vom folosi prima metodă pentru a rezolva acest sistem. Mai întâi, să exprimăm $y$ în prima ecuație în termeni de $x$.

Figura 2.
Înlocuiți $y$ în a doua ecuație:
\ \ \[-2-x=2\] \ \
Răspuns: $(-4,6)$.
Exemplul 2
Rezolvați un sistem de ecuații

Figura 3
Decizie.
Acest sistem este echivalent cu sistemul

Figura 4
Aplicam a patra metoda de rezolvare a ecuatiilor. Fie $2^x=u\ (u >0)$ și $3^y=v\ (v >0)$, obținem:

Figura 5
Rezolvăm sistemul rezultat prin metoda adunării. Să adăugăm ecuațiile:
\ \
Apoi, din a doua ecuație, obținem asta
Revenind la înlocuitor, am sistem nou ecuații exponențiale:
Figura 6
Primim:
Figura 7
Răspuns: $(0,1)$.
Sisteme de inegalități exponențiale
Definiția 2
Sistemele de inegalități formate din ecuații exponențiale se numesc un sistem de inegalități exponențiale.
Vom lua în considerare soluția sistemelor de inegalități exponențiale folosind exemple.
Exemplul 3
Rezolvați sistemul de inegalități

Figura 8
Decizie:
Acest sistem de inegalități este echivalent cu sistemul

Figura 9
Pentru a rezolva prima inegalitate, amintiți-vă următoarea teoremă de echivalență pentru inegalitățile exponențiale:
Teorema 1. Inegalitatea $a^(f(x)) >a^(\varphi (x)) $, unde $a >0,a\ne 1$ este echivalentă cu mulțimea a două sisteme
\}