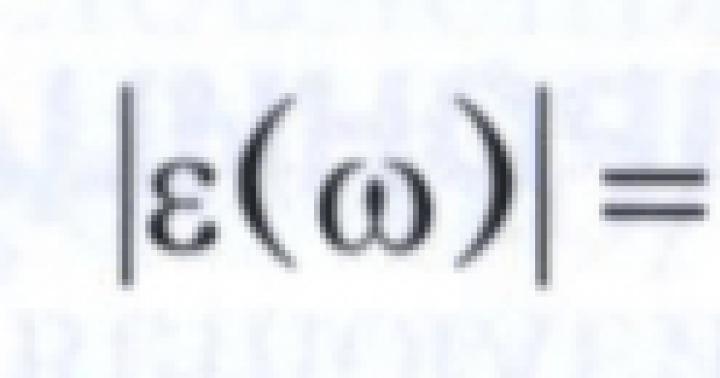Η γραμμή ανήκει στο αεροπλάνο, αν έχει δύο κοινά σημεία ή ένα κοινό σημείο και είναι παράλληλη με κάποια ευθεία που βρίσκεται στο επίπεδο. Αφήστε το επίπεδο στο σχέδιο να δοθεί από δύο τεμνόμενες ευθείες γραμμές. Σε αυτό το επίπεδο, απαιτείται να κατασκευαστούν δύο γραμμές m και n σύμφωνα με αυτές τις συνθήκες ( σολ(α β)) (Εικ. 4.5).
Λύση 1. Σχεδιάστε αυθαίρετα m 2, αφού η ευθεία ανήκει στο επίπεδο, σημειώστε τις προβολές των σημείων τομής της με τις ευθείες ένακαι σικαι προσδιορίστε τις οριζόντιες προβολές τους, σχεδιάστε m 1 έως 1 1 και 2 1.
2. Μέσα από το σημείο Στο επίπεδο σχεδιάζουμε n 2 ║m 2 και n 1 ║m 1.
Ευθεία παράλληλη στο επίπεδοεάν είναι παράλληλη με οποιαδήποτε ευθεία που βρίσκεται στο επίπεδο.
Τομή γραμμής και επιπέδου.Υπάρχουν τρεις περιπτώσεις εντοπισμού μιας ευθείας γραμμής και ενός επιπέδου σε σχέση με τα επίπεδα προβολής. Ανάλογα με αυτό προσδιορίζεται το σημείο τομής της ευθείας και του επιπέδου.
Πρώτη περίπτωση
- ευθεία και επίπεδο - θέση προβολής. Σε αυτή την περίπτωση, υπάρχει ένα σημείο τομής στο σχέδιο (και οι δύο προβολές του), χρειάζεται μόνο να επισημανθεί.
ΠΑΡΑΔΕΙΓΜΑ Στο σχέδιο, το επίπεδο δίνεται με ίχνη Σ ( ω 0 f0)– οριζόντια θέση προβολής – και ευθεία μεγάλο- μετωπική προεξέχουσα θέση. Προσδιορίστε το σημείο τομής τους (Εικ. 4.6).
Υπάρχει ήδη ένα σημείο τομής στο σχέδιο - K (K 1 K 2).
Δεύτερη περίπτωση- ή ευθεία γραμμή, ή επίπεδο - της θέσης προβολής. Σε αυτήν την περίπτωση, σε ένα από τα επίπεδα προβολής, υπάρχει ήδη μια προβολή του σημείου τομής, πρέπει να οριστεί και στο δεύτερο επίπεδο προβολής, πρέπει να βρεθεί από το ανήκει.
ΠΑΡΑΔΕΙΓΜΑΤΑ. Στο σχ. 4.7, αλλά το επίπεδο απεικονίζεται με ίχνη μετωπικής προεξέχουσας θέσης και ευθείας γραμμής μεγάλο- γενική θέση. Η προβολή του σημείου τομής Κ 2 στο σχέδιο είναι ήδη διαθέσιμη και η προβολή Κ 1 πρέπει να βρεθεί αν ανήκει στο σημείο Κ στην ευθεία μεγάλο. Στο
ρύζι. 4.7, το b είναι ένα επίπεδο σε γενική θέση, και η ευθεία m προεξέχει μετωπικά, τότε το K 2 υπάρχει ήδη (συμπίπτει με το m 2) και το K 1 πρέπει να βρεθεί από την προϋπόθεση ότι το σημείο ανήκει στο επίπεδο. Για να το κάνετε αυτό, περάστε από το Κ
ευθεία ( η- οριζόντια) που βρίσκεται σε ένα επίπεδο.
Τρίτη περίπτωση- και ευθεία και επίπεδο - γενικής θέσης. Σε αυτή την περίπτωση, για να προσδιορίσετε το σημείο τομής μιας ευθείας γραμμής και ενός επιπέδου, είναι απαραίτητο να χρησιμοποιήσετε τον λεγόμενο μεσολαβητή - το προεξέχον επίπεδο. Για να γίνει αυτό, ένα βοηθητικό επίπεδο τομής σχεδιάζεται μέσω της ευθείας γραμμής. Αυτό το επίπεδο τέμνει το δεδομένο επίπεδο κατά μήκος της γραμμής. Αν αυτή η ευθεία τέμνει μια δεδομένη ευθεία, τότε υπάρχει ένα σημείο τομής της ευθείας και του επιπέδου.
ΠΑΡΑΔΕΙΓΜΑΤΑ. Στο σχ. 4.8 το επίπεδο παριστάνεται από ένα τρίγωνο ABC - σε γενική θέση - και μια ευθεία γραμμή μεγάλο- γενική θέση. Για τον προσδιορισμό του σημείου τομής Κ, είναι απαραίτητο μέσω μεγάλοσχεδιάστε ένα μετωπικά προεξέχον επίπεδο Σ, κατασκευάστε μια ευθεία τομής των Δ και Σ στο τρίγωνο (στο σχέδιο αυτό είναι ένα τμήμα 1.2), προσδιορίστε το K 1 και με το να ανήκετε - K 2. Στη συνέχεια προσδιορίζεται η ορατότητα της γραμμής μεγάλοως προς το τρίγωνο από ανταγωνιστικά σημεία. Στο P 1, τα σημεία 3 και 4 λαμβάνονται ως ανταγωνιστικά σημεία. Η προβολή του σημείου 4 είναι ορατή στο P 1, αφού η συντεταγμένη του Z είναι μεγαλύτερη από αυτή του σημείου 3, επομένως, η προβολή l 1από αυτό το σημείο μέχρι το Κ 1 θα είναι αόρατο.
Ανταγωνιστικά σημεία στο P 2 είναι το σημείο 1, που ανήκει στο ΑΒ, και το σημείο 5, που ανήκει μεγάλο. Το σημείο 1 θα είναι ορατό, καθώς η συντεταγμένη του Υ είναι μεγαλύτερη από αυτή του σημείου 5, και επομένως η προβολή της ευθείας l 2μέχρι το Κ 2 είναι αόρατο.
Το άρθρο μιλά για την έννοια της ευθείας γραμμής σε ένα επίπεδο. Εξετάστε τους βασικούς όρους και τις ονομασίες τους. Ας δουλέψουμε με την αμοιβαία διάταξη μιας γραμμής και ενός σημείου και δύο ευθειών σε ένα επίπεδο. Ας μιλήσουμε για αξιώματα. Ως αποτέλεσμα, θα συζητήσουμε μεθόδους και μεθόδους για τον καθορισμό μιας ευθείας γραμμής σε ένα επίπεδο.
Γραμμή στο αεροπλάνο - η έννοια
Πρώτα πρέπει να έχετε μια ξεκάθαρη ιδέα για το τι είναι αεροπλάνο. Οποιαδήποτε επιφάνεια κάτι μπορεί να αποδοθεί σε ένα επίπεδο, μόνο που διαφέρει από τα αντικείμενα στο άπειρό της. Αν φανταστούμε ότι το αεροπλάνο είναι τραπέζι, τότε στην περίπτωσή μας δεν θα έχει όρια, αλλά θα είναι απείρως τεράστιο.
Εάν αγγίξετε το τραπέζι με ένα μολύβι, θα παραμείνει ένα σημάδι, το οποίο μπορεί να ονομαστεί "κουκκίδα". Έτσι, παίρνουμε μια ιδέα ενός σημείου σε ένα επίπεδο.
Εξετάστε την έννοια της ευθείας γραμμής σε ένα επίπεδο. Εάν σχεδιάσετε μια ευθεία γραμμή σε ένα φύλλο, τότε θα εμφανιστεί σε αυτό με περιορισμένο μήκος. Δεν πήραμε ολόκληρη τη γραμμή, αλλά μόνο ένα μέρος της, αφού στην πραγματικότητα δεν έχει τέλος, όπως το αεροπλάνο. Επομένως, η εικόνα των γραμμών και των επιπέδων σε ένα σημειωματάριο είναι επίσημη.
Έχουμε ένα αξίωμα:
Ορισμός 1
Τα σημεία μπορούν να σημειωθούν σε κάθε γραμμή και σε κάθε επίπεδο.
Τα σημεία υποδηλώνονται με μεγάλα και μικρά λατινικά γράμματα. Για παράδειγμα, Α και Δ ή α και δ.
Για ένα σημείο και μια γραμμή, είναι γνωστές μόνο δύο παραλλαγές θέσης: ένα σημείο σε μια ευθεία, με άλλα λόγια, ότι η γραμμή διέρχεται από αυτό, ή ένα σημείο που δεν βρίσκεται στη γραμμή, δηλαδή, η γραμμή δεν διέρχεται από αυτήν .
Για να υποδείξετε αν ανήκει ένα σημείο σε επίπεδο ή σημείο σε ευθεία, χρησιμοποιήστε το σύμβολο "∈". Αν δίνεται με την προϋπόθεση ότι το σημείο Α βρίσκεται στην ευθεία a , τότε έχει τη μορφή A ∈ a . Στην περίπτωση που το σημείο Α δεν ανήκει, τότε μια άλλη εγγραφή είναι A ∉ a .
Δίκαιη κρίση:
Ορισμός 2
Διαμέσου οποιωνδήποτε δύο σημείων σε οποιοδήποτε επίπεδο, υπάρχει μόνο μία γραμμή που διέρχεται από αυτά.
Αυτή η δήλωση θεωρείται αισιόδοξη, επομένως δεν απαιτεί απόδειξη. Εάν το αναλογιστείτε μόνοι σας, μπορείτε να δείτε ότι με τα δύο υπάρχοντα σημεία, υπάρχει μόνο μία επιλογή για τη σύνδεσή τους. Εάν έχουμε δύο δεδομένα σημεία Α και Β, τότε η ευθεία που διέρχεται από αυτά μπορεί να ονομαστεί αυτά τα γράμματα, για παράδειγμα, η ευθεία Α Β. Σκεφτείτε το παρακάτω σχήμα.
Μια ευθεία γραμμή σε ένα επίπεδο έχει ένας μεγάλος αριθμός απόσημεία. Από εδώ προέρχεται το αξίωμα:
Ορισμός 3
Εάν δύο σημεία μιας ευθείας βρίσκονται σε ένα επίπεδο, τότε όλα τα άλλα σημεία της ευθείας βρίσκονται στο επίπεδο.
Το σύνολο των σημείων μεταξύ δύο δεδομένων σημείων ονομάζεται ένα ευθύγραμμο τμήμα.Έχει αρχή και τέλος. Χαρακτηρίζεται με δύο γράμματα.
Εάν δοθεί ότι τα σημεία Α και Ρ είναι τα άκρα του τμήματος, τότε ο χαρακτηρισμός του θα πάρει τη μορφή Р А ή А Р. Επειδή οι χαρακτηρισμοί του τμήματος και της γραμμής συμπίπτουν, συνιστάται να προσθέσετε ή να ολοκληρώσετε τις λέξεις " τμήμα», «ευθεία γραμμή».
Η συνοπτική σημείωση της ιδιότητας μέλους περιλαμβάνει τη χρήση των σημείων ∈ και ∉ . Για να καθορίσετε τη θέση του τμήματος σε σχέση με μια δεδομένη ευθεία, χρησιμοποιήστε το ⊂ . Αν δίνεται υπό την προϋπόθεση ότι το τμήμα А Р ανήκει στην ευθεία b, τότε η εγγραφή θα μοιάζει με αυτό: А Р ⊂ b.
Συμβαίνει η περίπτωση να ανήκουν τρία σημεία σε μία ευθεία ταυτόχρονα. Αυτό ισχύει όταν ένα σημείο βρίσκεται ανάμεσα σε δύο άλλα. Αυτή η δήλωση θεωρείται αξίωμα. Αν δοθούν τα σημεία Α, Β, Γ που ανήκουν στην ίδια ευθεία και το σημείο Β βρίσκεται μεταξύ Α και Γ, έπεται ότι όλα τα δεδομένα βρίσκονται στην ίδια ευθεία, αφού βρίσκονται και στις δύο πλευρές του σημείου Β.
Το σημείο χωρίζει την ευθεία σε δύο μέρη, που ονομάζονται ακτίνες.Έχουμε ένα αξίωμα:
Ορισμός 4
Οποιοδήποτε σημείο βρίσκεται σε μια γραμμή τη χωρίζει σε δύο ακτίνες και οποιαδήποτε δύο σημεία μιας ακτίνας βρίσκονται στη μία πλευρά της ακτίνας σε σχέση με το σημείο Ο και τα άλλα βρίσκονται στην άλλη πλευρά της ακτίνας.
Η διάταξη των ευθειών σε ένα επίπεδο μπορεί να έχει τη μορφή δύο καταστάσεων.
Ορισμός 5
συμπίπτω.
Αυτή η πιθανότητα εμφανίζεται όταν οι γραμμές έχουν κοινά σημεία. Με βάση το αξίωμα που γράφτηκε παραπάνω, έχουμε ότι μια ευθεία διέρχεται από δύο σημεία και μόνο ένα. Αυτό σημαίνει ότι όταν 2 γραμμές περνούν από τα δεδομένα 2 σημεία, συμπίπτουν.
Ορισμός 6
Δύο ευθείες σε ένα επίπεδο σταυρός.
Αυτή η περίπτωση δείχνει ότι υπάρχει ένα κοινό σημείο, το οποίο ονομάζεται τομή γραμμών. Η τομή συμβολισμού εισάγεται με το σύμβολο ∩ . Αν υπάρχει μορφή a ∩ b = M , τότε προκύπτει ότι οι δεδομένες ευθείες a και b τέμνονται στο σημείο M .
Στη διασταύρωση των ευθειών, ασχολούμαστε με τη σχηματισμένη γωνία. Ξεχωριστή εξέταση δίνεται στο τμήμα της τομής των γραμμών σε ένα επίπεδο με το σχηματισμό γωνίας 90 μοιρών, δηλαδή ορθής γωνίας. Τότε οι ευθείες λέγονται κάθετες.Η μορφή γραφής δύο κάθετων ευθειών είναι: a ⊥ b, που σημαίνει ότι η ευθεία α είναι κάθετη στην ευθεία β.
Ορισμός 7
Δύο ευθείες σε ένα επίπεδο μπορεί να είναι είναι παράλληλες.
Μόνο αν δύο δεδομένες ευθείες δεν έχουν κοινές τομές και επομένως δεν έχουν σημεία, είναι παράλληλες. Χρησιμοποιείται συμβολισμός που μπορεί να γραφτεί για δεδομένο παραλληλισμό των ευθειών a και b: a ∥ b .
Μια ευθεία γραμμή σε ένα επίπεδο θεωρείται μαζί με διανύσματα. Ιδιαίτερη σημασία αποδίδεται στα μηδενικά διανύσματα που βρίσκονται σε μια δεδομένη ευθεία ή σε οποιαδήποτε από τις παράλληλες ευθείες, ονομάζονται διανύσματα κατεύθυνσης της ευθείας. Σκεφτείτε το παρακάτω σχήμα.
Τα μη μηδενικά διανύσματα που βρίσκονται σε ευθείες κάθετες στη δεδομένη ονομάζονται αλλιώς κανονικά διανύσματα της ευθείας. Υπάρχει μια λεπτομερής περιγραφή στο άρθρο κανονικό διάνυσμα μιας ευθείας γραμμής σε ένα επίπεδο. Σκεφτείτε το παρακάτω σχήμα.
Εάν δίνονται 3 γραμμές σε ένα αεροπλάνο, η θέση τους μπορεί να είναι πολύ διαφορετική. Υπάρχουν πολλές επιλογές για τη θέση τους: η τομή όλων, ο παραλληλισμός ή η παρουσία διαφορετικών σημείων τομής. Το σχήμα δείχνει την κάθετη τομή δύο ευθειών ως προς τη μία.
Για να γίνει αυτό, παρουσιάζουμε τους απαραίτητους παράγοντες που αποδεικνύουν τη σχετική τους θέση:
- αν δύο ευθείες είναι παράλληλες με μια τρίτη, τότε είναι όλες παράλληλες.
- αν δύο ευθείες είναι κάθετες σε μια τρίτη, τότε οι δύο ευθείες είναι παράλληλες.
- Αν μια ευθεία τέμνει μια παράλληλη ευθεία σε ένα επίπεδο, τότε τέμνει μια άλλη.
Ας ρίξουμε μια ματιά στις εικόνες.
Μια ευθεία γραμμή σε ένα επίπεδο μπορεί να οριστεί με διάφορους τρόπους. Όλα εξαρτώνται από την κατάσταση του προβλήματος και από το τι θα βασίζεται η επίλυσή του. Αυτή η γνώση μπορεί να βοηθήσει στην πρακτική θέση των γραμμών.
Ορισμός 8
Η ευθεία γραμμή ορίζεται χρησιμοποιώντας τα υποδεικνυόμενα δύο σημεία που βρίσκονται στο επίπεδο.
Από το εξεταζόμενο αξίωμα προκύπτει ότι μέσω δύο σημείων είναι δυνατό να χαράξουμε μια ευθεία γραμμή και, επιπλέον, μια μόνο γραμμή. Όταν ένα ορθογώνιο σύστημα συντεταγμένων καθορίζει τις συντεταγμένες δύο σημείων που δεν συμπίπτουν, τότε είναι δυνατό να καθοριστεί η εξίσωση μιας ευθείας που διέρχεται από δύο δεδομένα σημεία. Θεωρήστε ένα σχήμα όπου έχουμε μια ευθεία που διέρχεται από δύο σημεία. 
Ορισμός 9
Μια ευθεία μπορεί να οριστεί μέσω ενός σημείου και μιας ευθείας στην οποία είναι παράλληλη.
Αυτή η μέθοδος έχει τόπο ύπαρξης, αφού μέσω ενός σημείου είναι δυνατό να χαράξουμε μια ευθεία γραμμή παράλληλη με τη δεδομένη και μόνο μία. Η απόδειξη είναι γνωστή από σχολικό μάθημακατά γεωμετρία.
Εάν η ευθεία δίνεται σε σχέση με το καρτεσιανό σύστημα συντεταγμένων, τότε είναι δυνατό να διατυπωθεί η εξίσωση μιας ευθείας που διέρχεται από ένα δεδομένο σημείο παράλληλο σε μια δεδομένη ευθεία. Εξετάστε την αρχή του καθορισμού μιας ευθείας γραμμής σε ένα επίπεδο.
Ορισμός 10
Η γραμμή καθορίζεται μέσω του καθορισμένου διανύσματος σημείου και κατεύθυνσης.
Όταν δίνεται μια ευθεία γραμμή σε ένα ορθογώνιο σύστημα συντεταγμένων, είναι δυνατό να συνθέσουμε κανονικές και παραμετρικές εξισώσεις σε ένα επίπεδο. Θεωρήστε στο σχήμα τη θέση της ευθείας με την παρουσία ενός διανύσματος κατεύθυνσης.
Το τέταρτο σημείο του καθορισμού μιας ευθείας γραμμής έχει νόημα όταν υποδεικνύεται ένα σημείο από το οποίο πρέπει να τραβηχτεί και μια ευθεία γραμμή κάθετη σε αυτήν. Από το αξίωμα έχουμε:
Ορισμός 11
Από ένα δεδομένο σημείο που βρίσκεται σε ένα επίπεδο, θα περάσει μόνο μία ευθεία, κάθετη στη δεδομένη.
Και το τελευταίο σημείο που σχετίζεται με την αντιστοίχιση μιας ευθείας γραμμής σε ένα επίπεδο βρίσκεται σε ένα καθορισμένο σημείο από το οποίο διέρχεται η ευθεία, και παρουσία ενός κανονικού διανύσματος της ευθείας. Με γνωστές συντεταγμένες ενός σημείου που βρίσκεται σε μια δεδομένη ευθεία γραμμή, και τις συντεταγμένες ενός κανονικού διανύσματος, είναι δυνατόν να γραφτεί η γενική εξίσωση μιας ευθείας γραμμής.
Εάν παρατηρήσετε κάποιο λάθος στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter
Η γραμμή μπορεί να ανήκει ή να μην ανήκει στο αεροπλάνο. Ανήκει στο επίπεδο εάν τουλάχιστον δύο από τα σημεία του βρίσκονται στο επίπεδο. Το σχήμα 93 δείχνει το επίπεδο άθροισμα (axb).Ευθεία μεγάλοανήκει στο επίπεδο Άθροισμα, αφού τα σημεία 1 και 2 του ανήκουν σε αυτό το επίπεδο.
Εάν η ευθεία δεν ανήκει στο επίπεδο, μπορεί να είναι παράλληλη με αυτό ή να το τέμνει.
Μια ευθεία είναι παράλληλη σε ένα επίπεδο εάν είναι παράλληλη με μια άλλη ευθεία σε αυτό το επίπεδο. Εικόνα 93 ευθεία m || άθροισμα, αφού είναι παράλληλη με την ευθεία μεγάλοπου ανήκουν σε αυτό το αεροπλάνο.
Μια ευθεία γραμμή μπορεί να τέμνει ένα επίπεδο σε διάφορες γωνίες και, ειδικότερα, να είναι κάθετη σε αυτό. Η κατασκευή γραμμών τομής ευθείας με επίπεδο δίνεται στην §61.
Εικόνα 93 - Μια ευθεία γραμμή που ανήκει σε ένα επίπεδο
Ένα σημείο σε σχέση με ένα επίπεδο μπορεί να βρίσκεται ως εξής: να ανήκεις ή να μην ανήκεις σε αυτό. Ένα σημείο ανήκει σε ένα επίπεδο εάν βρίσκεται σε μια γραμμή σε αυτό το επίπεδο. Το σχήμα 94 δείχνει ένα σύνθετο σχέδιο του επιπέδου αθροίσματος που ορίζεται από δύο παράλληλες ευθείες μεγάλοκαι Π.Η γραμμή είναι στο αεροπλάνο Μ.Το σημείο Α βρίσκεται στο επίπεδο Άθροισμα, αφού βρίσκεται στην ευθεία Μ.Τελεία ΣΤΟδεν ανήκει στο επίπεδο, αφού η δεύτερη προβολή του δεν βρίσκεται στις αντίστοιχες προεξοχές της γραμμής.
Εικόνα 94 - Σύνθετο σχέδιο ενός επιπέδου που ορίζεται από δύο παράλληλες γραμμές
Κωνικές και κυλινδρικές επιφάνειες
Οι κωνικές επιφάνειες περιλαμβάνουν επιφάνειες που σχηματίζονται από τη μετατόπιση μιας ευθύγραμμης γεννήτριας μεγάλοκατά μήκος ενός κυρτού οδηγού Μ.Ένα χαρακτηριστικό του σχηματισμού μιας κωνικής επιφάνειας είναι ότι σε αυτήν την περίπτωση ένα σημείο της γεννήτριας είναι πάντα σταθερό. Αυτό το σημείο είναι η κορυφή της κωνικής επιφάνειας (Εικόνα 95, ένα).Ο οριστής κωνικής επιφάνειας περιλαμβάνει κορυφή μικρόκαι οδηγός Μ,εν μεγάλο"~S; μεγάλο"^ Μ.
Οι κυλινδρικές επιφάνειες περιλαμβάνουν επιφάνειες που σχηματίζονται από μια ευθεία γεννήτρια / κινούνται κατά μήκος ενός καμπυλόγραμμου οδηγού tπαράλληλα με τη δεδομένη κατεύθυνση μικρό(Εικόνα 95, σι).Μια κυλινδρική επιφάνεια μπορεί να θεωρηθεί ως ειδική περίπτωση κωνικής επιφάνειας με κορυφή στο άπειρο ΜΙΚΡΟ.
Ο καθοριστικός παράγοντας κυλινδρικής επιφάνειας αποτελείται από έναν οδηγό tκαι κατεύθυνση S, σχηματισμός μεγάλο, ενώ λ" || ΜΙΚΡΟ; l" ^ m.
Εάν οι γεννήτριες μιας κυλινδρικής επιφάνειας είναι κάθετες στο επίπεδο των προεξοχών, τότε μια τέτοια επιφάνεια ονομάζεται προβάλλοντας.Εικόνα 95, σεεμφανίζεται μια οριζόντια προεξέχουσα κυλινδρική επιφάνεια.
Σε κυλινδρικές και κωνικές επιφάνειες, τα συγκεκριμένα σημεία κατασκευάζονται χρησιμοποιώντας γεννήτριες που διέρχονται από αυτά. Γραμμές σε επιφάνειες, όπως μια γραμμή έναστο σχήμα 95, σεή οριζόντια ηστο σχήμα 95, α, β,κατασκευάζονται χρησιμοποιώντας μεμονωμένα σημεία που ανήκουν σε αυτές τις γραμμές.
Εικόνα 95 - Κωνικές και κυλινδρικές επιφάνειες
Επιφάνειες κορμού
Η επιφάνεια του κορμού είναι μια επιφάνεια που σχηματίζεται από μια ευθύγραμμη γεννήτρια μεγάλο, αγγίζοντας κατά την κίνησή του σε όλες τις θέσεις του μια ορισμένη χωρική καμπύλη t,που ονομάζεται άκρη επιστροφής(Εικόνα 96). Το άκρο επιστροφής ορίζει πλήρως τον κορμό και είναι το γεωμετρικό τμήμα του προσδιοριστή επιφάνειας. Το αλγοριθμικό μέρος είναι η ένδειξη της εφαπτομένης των γεννητριών στο άκρο του άκρου.
Μια κωνική επιφάνεια είναι μια ειδική περίπτωση κορμού με ακμή επιστροφής tεκφυλίστηκε σε ένα σημείο μικρό- κορυφή κωνικής επιφάνειας. Μια κυλινδρική επιφάνεια είναι μια ειδική περίπτωση ενός κορμού, του οποίου η ακμή είναι ένα σημείο στο άπειρο.
Εικόνα 96 - Επιφάνεια κορμού
Πολυεπίπεδες επιφάνειες
Οι επιφάνειες με όψη περιλαμβάνουν επιφάνειες που σχηματίζονται από τη μετατόπιση μιας ευθύγραμμης γεννήτριας μεγάλοκατά μήκος μιας διακεκομμένης γραμμής Μ.Ωστόσο, αν ένα σημείο μικρόΗ γεννήτρια είναι ακίνητη, δημιουργείται μια πυραμιδική επιφάνεια (Εικόνα 97) εάν η γεννήτρια είναι παράλληλη σε μια δεδομένη κατεύθυνση όταν κινείται ΜΙΚΡΟ,τότε δημιουργείται πρισματική επιφάνεια (Εικόνα 98).
Τα στοιχεία των πολύπλευρων επιφανειών είναι: κορυφή μικρό(κοντά στην πρισματική επιφάνεια βρίσκεται στο άπειρο), πρόσωπο (μέρος του επιπέδου που οριοθετείται από ένα τμήμα του οδηγού Μκαι τις ακραίες θέσεις της γεννήτριας σε σχέση με αυτήν μεγάλο) και μια άκρη (γραμμή τομής παρακείμενων όψεων).
Ο προσδιοριστής επιφάνειας πυραμίδας περιλαμβάνει κορυφή ΜΙΚΡΟ,μέσω των οποίων διέρχονται γεννήτριες και οδηγοί: μεγάλο" ~ ΜΙΚΡΟ; μεγάλο^ t.
Καθοριστικό πρισματικής επιφάνειας, εκτός από τον οδηγό t,περιέχει κατεύθυνση ΜΙΚΡΟ,στην οποία όλες οι γεννήτριες είναι παράλληλες μεγάλοεπιφάνειες: l||S; l^ t.
Εικόνα 97 - Πυραμιδική επιφάνεια
Εικόνα 98 - Πρισματική επιφάνεια
Οι κλειστές πολύπλευρες επιφάνειες που σχηματίζονται από έναν ορισμένο αριθμό (τουλάχιστον τέσσερις) όψεις ονομάζονται πολύεδρα. Μεταξύ των πολύεδρων, διακρίνεται μια ομάδα κανονικών πολύεδρων, στην οποία όλες οι όψεις είναι κανονικά και ομοιόμορφα πολύγωνα και οι πολυεδρικές γωνίες στις κορυφές είναι κυρτές και περιέχουν τον ίδιο αριθμό όψεων. Για παράδειγμα: εξάεδρο - κύβος (Εικόνα 99, ένα),τετράεδρο - κανονικό τετράγωνο (Εικόνα 99, 6) οκτάεδρο - πολύεδρο (Εικόνα 99, σε).Οι κρύσταλλοι έχουν το σχήμα διαφόρων πολύεδρων.
Εικόνα 99 - Πολύεδρα
Πυραμίδα- ένα πολύεδρο, στη βάση του οποίου βρίσκεται ένα αυθαίρετο πολύγωνο και οι πλευρικές όψεις είναι τρίγωνα με κοινή κορυφή ΜΙΚΡΟ.
Στο σύνθετο σχέδιο, η πυραμίδα ορίζεται από τις προεξοχές των κορυφών και των άκρων της, λαμβάνοντας υπόψη την ορατότητά τους. Η ορατότητα μιας άκρης προσδιορίζεται χρησιμοποιώντας ανταγωνιστικά σημεία (Εικόνα 100).
Εικόνα 100 - Προσδιορισμός της ορατότητας μιας ακμής χρησιμοποιώντας ανταγωνιστικά σημεία
Πρίσμα- ένα πολύεδρο του οποίου η βάση είναι δύο πανομοιότυπα και αμοιβαία παράλληλα πολύγωνα και οι πλευρικές όψεις είναι παραλληλόγραμμα. Αν οι ακμές του πρίσματος είναι κάθετες στο επίπεδο της βάσης, ένα τέτοιο πρίσμα ονομάζεται ευθεία γραμμή. Αν οι ακμές ενός πρίσματος είναι κάθετες σε οποιοδήποτε επίπεδο προβολής, τότε πλευρική επιφάνειαλέγεται προβολικός. Το Σχήμα 101 δείχνει ένα σύνθετο σχέδιο ενός ευθύγραμμου τετραγωνικού πρίσματος με μια οριζόντια προεξέχουσα επιφάνεια.
Εικόνα 101 - Σύνθετο σχέδιο ευθύγραμμου τετραγωνικού πρίσματος με οριζόντια προεξέχουσα επιφάνεια
Όταν εργάζεστε με ένα σύνθετο σχέδιο ενός πολυέδρου, πρέπει να δημιουργήσετε γραμμές στην επιφάνειά του και δεδομένου ότι μια γραμμή είναι μια συλλογή σημείων, πρέπει να μπορείτε να δημιουργήσετε σημεία στην επιφάνεια.
Οποιοδήποτε σημείο σε μια πολύπλευρη επιφάνεια μπορεί να κατασκευαστεί χρησιμοποιώντας μια γεννήτρια που διέρχεται από αυτό το σημείο. Στο σχήμα 100 στο πρόσωπο ACSσημείο χτισμένο Μμε τη βοήθεια της γεννήτριας S-5.
Ελικοειδείς επιφάνειες
Οι ελικοειδείς επιφάνειες είναι εκείνες που δημιουργούνται κατά την ελικοειδή κίνηση μιας ευθύγραμμης γεννήτριας. Οι ελικοειδείς επιφάνειες με κυβερνήτη ονομάζονται ελικοειδών.
Ένα ευθύ ελικοειδές σχηματίζεται από την κίνηση μιας ευθύγραμμης γεννήτριας Εγώκατά μήκος δύο οδηγών: μια έλικα tκαι τους άξονές του Εγώ; κατά την παραγωγή μεγάλοδιασχίζει τον ελικοειδή άξονα σε ορθή γωνία (Εικόνα 102, α). Ένα ευθύ ελικοειδές χρησιμοποιείται για τη δημιουργία σπειροειδών σκαλοπατιών, βιδών, καθώς και ηλεκτρικών σπειρωμάτων, σε εργαλειομηχανές.
Ένα κεκλιμένο ελικοειδές σχηματίζεται από την κίνηση της γεννήτριας κατά μήκος του ελικοειδούς οδηγού tκαι τους άξονές του Εγώώστε η γεννήτρια μεγάλοδιασχίζει τον άξονα Εγώσε σταθερή γωνία φ εκτός από ορθή γωνία, δηλαδή σε οποιαδήποτε θέση, η γεννήτρια μεγάλοπαράλληλη σε μία από τις γεννείες του κώνου οδήγησης με γωνία στην κορυφή ίση με 2φ (Εικόνα 102, σι).Τα κεκλιμένα ελικοειδή περιορίζουν τις επιφάνειες των νημάτων.
Εικόνα 102 - Ελικοειδή
Επιφάνειες επανάστασης
Οι επιφάνειες περιστροφής περιλαμβάνουν επιφάνειες που σχηματίζονται από την περιστροφή μιας γραμμής μεγάλο γύρω από μια ευθεία γραμμή Εγώ που αντιπροσωπεύει τον άξονα περιστροφής. Μπορούν να είναι κυβερνητικοί, όπως ένας κώνος ή κύλινδρος περιστροφής, και μη γραμμικοί ή καμπυλόγραμμοι, όπως μια σφαίρα. Ο προσδιοριστής της επιφάνειας της περιστροφής περιλαμβάνει τη γεννήτρια μεγάλο και άξονα Εγώ . Κάθε σημείο της γεννήτριας κατά την περιστροφή περιγράφει έναν κύκλο, το επίπεδο του οποίου είναι κάθετο στον άξονα περιστροφής. Τέτοιοι κύκλοι της επιφάνειας της περιστροφής ονομάζονται παράλληλοι. Ο μεγαλύτερος από τους παραλλήλους λέγεται ισημερινός.Ισημερινός.ορίζει το οριζόντιο περίγραμμα της επιφάνειας εάν i _|_ P 1 . Σε αυτή την περίπτωση, οι παράλληλοι είναι οι οριζόντιες της επιφάνειας αυτής.
Οι καμπύλες της επιφάνειας περιστροφής, που σχηματίζονται ως αποτέλεσμα της τομής της επιφάνειας με επίπεδα που διέρχονται από τον άξονα περιστροφής, ονομάζονται μεσημβρινοί.Όλοι οι μεσημβρινοί μιας επιφάνειας είναι ίσοι. Ο μετωπικός μεσημβρινός ονομάζεται κύριος μεσημβρινός. ορίζει το μετωπικό περίγραμμα της επιφάνειας της επανάστασης. Ο μεσημβρινός προφίλ καθορίζει το περίγραμμα προφίλ της επιφάνειας περιστροφής.
Είναι πιο βολικό να χτίσετε ένα σημείο σε καμπύλες επιφάνειες περιστροφής χρησιμοποιώντας παράλληλους επιφανειών. Εικόνα 103 τελεία Μχτισμένο στον παράλληλο h 4 .
Εικόνα 103 - Χτίζοντας ένα σημείο σε μια καμπύλη επιφάνεια
Οι επιφάνειες της επανάστασης έχουν βρει την ευρύτερη εφαρμογή στη μηχανική. Περιορίζουν τις επιφάνειες των περισσότερων εξαρτημάτων μηχανικής.
Μια κωνική επιφάνεια περιστροφής σχηματίζεται από την περιστροφή μιας ευθείας γραμμής Εγώγύρω από την ευθεία που τέμνεται με αυτό - τον άξονα Εγώ(Εικόνα 104, ένα). Τελεία Μστην επιφάνεια είναι χτισμένο χρησιμοποιώντας μια γεννήτρια μεγάλοκαι παράλληλες η.Αυτή η επιφάνεια ονομάζεται επίσης κώνος περιστροφής ή δεξιός κυκλικός κώνος.
Μια κυλινδρική επιφάνεια περιστροφής σχηματίζεται από την περιστροφή μιας ευθείας γραμμής μεγάλογύρω από έναν παράλληλο άξονα Εγώ(Εικόνα 104, σι).Αυτή η επιφάνεια ονομάζεται επίσης κύλινδρος ή δεξιός κυκλικός κύλινδρος.
Μια σφαίρα σχηματίζεται περιστρέφοντας έναν κύκλο γύρω από τη διάμετρό της (Εικόνα 104, σε). Το σημείο Α στην επιφάνεια της σφαίρας ανήκει στον πρώτο μεσημβρινό φά,τελεία ΣΤΟ- ισημερινός η,μια τελεία Μχτισμένο σε βοηθητικό παράλληλο η".
Εικόνα 104 - Σχηματισμός επιφανειών περιστροφής
Ένας δακτύλιος σχηματίζεται με την περιστροφή ενός κύκλου ή του τόξου του γύρω από έναν άξονα που βρίσκεται στο επίπεδο του κύκλου. Εάν ο άξονας βρίσκεται εντός του σχηματιζόμενου κύκλου, τότε ένας τέτοιος τόρος ονομάζεται κλειστός (Εικόνα 105, α). Εάν ο άξονας περιστροφής είναι έξω από τον κύκλο, τότε ένας τέτοιος τόρος ονομάζεται ανοιχτός (Εικόνα 105, σι).Ένας ανοιχτός τόρος ονομάζεται επίσης δακτύλιος.
Εικόνα 105 - Σχηματισμός δακτύλου
Οι επιφάνειες περιστροφής μπορούν επίσης να σχηματιστούν από άλλες καμπύλες δεύτερης τάξης. Ελλειψοειδές της επανάστασης (Εικόνα 106, ένα)που σχηματίζεται από την περιστροφή μιας έλλειψης γύρω από έναν από τους άξονές της. παραβολοειδές της επανάστασης (Εικόνα 106, σι) - περιστροφή της παραβολής γύρω από τον άξονά της. υπερβολοειδές περιστροφής ενός φύλλου (Εικόνα 106, σε) σχηματίζεται από την περιστροφή της υπερβολής γύρω από τον νοητό άξονα και είναι δύο φύλλων (Εικόνα 106, σολ) - περιστροφή της υπερβολής γύρω από τον πραγματικό άξονα.
Εικόνα 106 - Σχηματισμός επιφανειών περιστροφής από καμπύλες δεύτερης τάξης
Στη γενική περίπτωση, οι επιφάνειες απεικονίζονται ως μη περιορισμένες στην κατεύθυνση διάδοσης των γραμμών παραγωγής (βλ. Σχήματα 97, 98). Για την επίλυση συγκεκριμένων προβλημάτων και την απόκτηση γεωμετρικά σχήματαπεριορίζεται σε αεροπλάνα κοπής. Για παράδειγμα, για να αποκτήσετε έναν κυκλικό κύλινδρο, είναι απαραίτητο να περιορίσετε το τμήμα της κυλινδρικής επιφάνειας με κομμένα επίπεδα (βλ. Εικόνα 104, σι).Ως αποτέλεσμα, παίρνουμε τις πάνω και κάτω βάσεις του. Εάν τα επίπεδα κοπής είναι κάθετα στον άξονα περιστροφής, ο κύλινδρος θα είναι ευθύς, εάν όχι, ο κύλινδρος θα είναι κεκλιμένος.
Για να αποκτήσετε έναν κυκλικό κώνο (δείτε σχήμα 104, ένα), πρέπει να κόψετε κατά μήκος της κορυφής και πέρα. Εάν το επίπεδο κοπής της βάσης του κυλίνδρου είναι κάθετο στον άξονα περιστροφής, ο κώνος θα είναι ευθύς, εάν όχι, θα είναι κεκλιμένος. Εάν και τα δύο επίπεδα κοπής δεν περάσουν από την κορυφή, ο κώνος θα περικοπεί.
Χρησιμοποιώντας το επίπεδο κοπής, μπορείτε να πάρετε ένα πρίσμα και μια πυραμίδα. Για παράδειγμα, μια εξαγωνική πυραμίδα θα είναι ευθεία εάν όλες οι άκρες της έχουν την ίδια κλίση προς το επίπεδο κοπής. Σε άλλες περιπτώσεις, θα είναι λοξό. Αν γίνει μεμε τη βοήθεια αεροπλάνων και κανένα από αυτά δεν περνά από την κορυφή - η πυραμίδα είναι κολοβωμένη.
Ένα πρίσμα (βλ. Εικόνα 101) μπορεί να ληφθεί περιορίζοντας ένα τμήμα της πρισματικής επιφάνειας με δύο επίπεδα κοπής. Εάν το επίπεδο κοπής είναι κάθετο στις άκρες, για παράδειγμα, ένα οκταγωνικό πρίσμα, είναι ευθύ, αν όχι κάθετο, είναι κεκλιμένο.
Επιλέγοντας την κατάλληλη θέση των επιπέδων κοπής, είναι δυνατό να ληφθούν διάφορα σχήματα γεωμετρικών σχημάτων ανάλογα με τις συνθήκες του προβλήματος που επιλύεται.
Αμοιβαία διάταξη δύο ευθειών
Οι παρακάτω ισχυρισμοί εκφράζουν τα απαραίτητα και επαρκή σημάδιααμοιβαία διάταξη δύο ευθειών στο χώρο που δίνονται από κανονικές εξισώσεις
ένα) Οι ευθείες τέμνονται, δηλ. μην ξαπλώνετε στο ίδιο αεροπλάνο.
σι) Οι ευθείες τέμνονται.
Αλλά τα διανύσματα και δεν είναι συγγραμμικά (αλλιώς οι συντεταγμένες τους είναι ανάλογες).
σε) Οι ευθείες είναι παράλληλες.
Τα διανύσματα και είναι συγγραμμικά, αλλά το διάνυσμα δεν είναι συγγραμμικό με αυτά.
σολ) Οι γραμμές συμπίπτουν.
Και τα τρία διανύσματα: , είναι συγγραμμικά.
Απόδειξη.Ας αποδείξουμε την επάρκεια των αναφερόμενων κριτηρίων
ένα) Εξετάστε το διάνυσμα και τα διανύσματα κατεύθυνσης δεδομένων γραμμών
τότε αυτά τα διανύσματα είναι μη ομοεπίπεδα, επομένως, αυτές οι γραμμές δεν βρίσκονται στο ίδιο επίπεδο.
σι) Εάν, τότε τα διανύσματα είναι ομοεπίπεδα, τότε αυτές οι ευθείες βρίσκονται στο ίδιο επίπεδο, και εφόσον στην περίπτωση ( σι) τα διανύσματα κατεύθυνσης και αυτές οι ευθείες θεωρούνται μη γραμμικές, τότε οι ευθείες τέμνονται.
σε) Εάν τα διανύσματα κατεύθυνσης και οι δεδομένες ευθείες είναι συγγραμμικές, τότε οι ευθείες είναι είτε παράλληλες είτε συμπίπτουν. Πότε ( σε) οι ευθείες είναι παράλληλες, γιατί Με την προϋπόθεση, το διάνυσμα, η αρχή του οποίου βρίσκεται στο σημείο της πρώτης γραμμής και το τέλος - στο σημείο της δεύτερης γραμμής, δεν είναι συγγραμμικό και.
δ) Αν όλα τα διανύσματα και είναι συγγραμμικά, τότε οι γραμμές συμπίπτουν.
Η αναγκαιότητα των χαρακτηριστικών αποδεικνύεται με αντίφαση.
Kletenik αρ. 1007
Οι παρακάτω προτάσεις δίνουν τις απαραίτητες και επαρκείς προϋποθέσεις για τη σχετική θέση της ευθείας που δίνεται από τις κανονικές εξισώσεις
και το επίπεδο που δίνεται από τη γενική εξίσωση
σε σχέση με ένα κοινό καρτεσιανό σύστημα συντεταγμένων.
Ένα επίπεδο και μια ευθεία τέμνονται:
Το επίπεδο και η ευθεία είναι παράλληλα:
Η γραμμή βρίσκεται στο αεροπλάνο:
Ας αποδείξουμε πρώτα την επάρκεια των υποδεικνυόμενων κριτηρίων. Γράφουμε τις εξισώσεις αυτής της ευθείας σε παραμετρική μορφή:
Αντικαθιστώντας στην εξίσωση (2 (επίπεδο)) τις συντεταγμένες ενός αυθαίρετου σημείου αυτής της ευθείας, που λαμβάνονται από τους τύπους (3), θα έχουμε:
1. Αν, τότε η εξίσωση (4) έχει σχετικά tμόνη απόφαση:
έτσι αυτή η γραμμή και δεδομένο αεροπλάνοέχουν μόνο ένα κοινό σημείο, δηλ. διατέμνω.
2. Αν, τότε η εξίσωση (4) δεν ικανοποιείται για καμία τιμή t, δηλ. Δεν υπάρχει σημείο σε μια δεδομένη ευθεία που να βρίσκεται σε ένα δεδομένο επίπεδο, επομένως, η δεδομένη ευθεία και το επίπεδο είναι παράλληλα.
3. Αν, τότε η εξίσωση (4) ικανοποιείται για οποιαδήποτε τιμή t, δηλ. όλα τα σημεία μιας δεδομένης ευθείας βρίσκονται σε ένα δεδομένο επίπεδο, άρα η δεδομένη ευθεία βρίσκεται σε ένα δεδομένο επίπεδο.
Οι επαρκείς προϋποθέσεις για την αμοιβαία θέση της γραμμής και του επιπέδου που καταλήξαμε είναι και οι δύο απαραίτητες και μπορούν να αποδειχθούν αμέσως με αντίφαση.
Από όσα αποδείχθηκαν προκύπτουν τα απαραίτητα και επαρκής κατάστασητο γεγονός ότι το διάνυσμα είναι ομοεπίπεδο με το επίπεδο που δίνεται από τη γενική εξίσωση ως προς το γενικό καρτεσιανό σύστημα συντεταγμένων.
