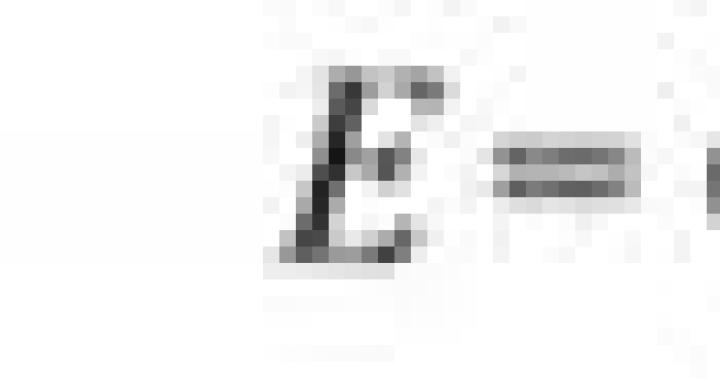Διασποράσυνεχής τυχαία μεταβλητήΤο X, οι πιθανές τιμές του οποίου ανήκουν σε ολόκληρο τον άξονα Ox, καθορίζεται από την ισότητα: ![]()
Ανάθεση υπηρεσίας. Ηλεκτρονική αριθμομηχανήσχεδιασμένο να επιλύει προβλήματα στα οποία είτε πυκνότητα κατανομής f(x) , ή συνάρτηση κατανομής F(x) (βλ. παράδειγμα). Συνήθως σε τέτοιες εργασίες απαιτείται να βρεθεί μαθηματική προσδοκία, τυπική απόκλιση, σχεδιάστε τις συναρτήσεις f(x) και F(x).
Εντολή. Επιλέξτε τον τύπο των δεδομένων εισόδου: πυκνότητα κατανομής f(x) ή συνάρτηση κατανομής F(x) .
Η πυκνότητα κατανομής f(x) δίνεται: 
Δίνεται η συνάρτηση κατανομής F(x): 
Μια συνεχής τυχαία μεταβλητή ορίζεται από μια πυκνότητα πιθανότητας 
(νόμος διανομής Rayleigh - χρησιμοποιείται στη ραδιομηχανική). Βρείτε M(x) , D(x) .
Καλείται η τυχαία μεταβλητή Χ συνεχής
, αν η συνάρτηση κατανομής της F(X)=P(X< x) непрерывна и имеет производную.
Η συνάρτηση κατανομής μιας συνεχούς τυχαίας μεταβλητής χρησιμοποιείται για τον υπολογισμό των πιθανοτήτων μιας τυχαίας μεταβλητής να εμπίπτει σε ένα δεδομένο διάστημα:
Ρ(α< X < β)=F(β) - F(α)
Επιπλέον, για μια συνεχή τυχαία μεταβλητή, δεν έχει σημασία αν τα όριά της περιλαμβάνονται σε αυτό το διάστημα ή όχι:
Ρ(α< X < β) = P(α ≤ X < β) = P(α ≤ X ≤ β)
Πυκνότητα κατανομής
Η συνεχής τυχαία μεταβλητή ονομάζεται συνάρτηση
f(x)=F'(x) , παράγωγος της συνάρτησης κατανομής.
Ιδιότητες πυκνότητας κατανομής
1. Η πυκνότητα κατανομής μιας τυχαίας μεταβλητής είναι μη αρνητική (f(x) ≥ 0) για όλες τις τιμές του x.2. Συνθήκη κανονικοποίησης:
Η γεωμετρική έννοια της συνθήκης κανονικοποίησης: η περιοχή κάτω από την καμπύλη πυκνότητας κατανομής είναι ίση με ένα.
3. Η πιθανότητα να χτυπηθεί μια τυχαία μεταβλητή Χ στο διάστημα από α έως β μπορεί να υπολογιστεί με τον τύπο
Γεωμετρικά, η πιθανότητα μια συνεχής τυχαία μεταβλητή Χ να πέσει στο διάστημα (α, β) είναι ίση με την περιοχή του καμπυλόγραμμου τραπεζοειδούς κάτω από την καμπύλη πυκνότητας κατανομής με βάση αυτό το διάστημα.
4. Η συνάρτηση κατανομής εκφράζεται ως προς την πυκνότητα ως εξής:
Η τιμή της πυκνότητας κατανομής στο σημείο x δεν είναι ίση με την πιθανότητα να ληφθεί αυτή η τιμή· για μια συνεχή τυχαία μεταβλητή, μπορούμε να μιλήσουμε μόνο για την πιθανότητα πτώσης σε ένα δεδομένο διάστημα. Έστω (Εικ. 5.4). Βρείτε μια αναλυτική έκφραση για την πυκνότητα πιθανότητας φά(Χ) στην ακέραια αριθμητική γραμμή.
Ρύζι. 5.4 Εικ. 5.5
5.16. Τυχαία τιμή Χκατανέμονται σύμφωνα με το νόμο ορθογώνιο τρίγωνο" στο διάστημα (0; 4) (Εικ. 5.5). Βρείτε μια αναλυτική έκφραση για την πυκνότητα πιθανότητας φά(Χ) στην ακέραια αριθμητική γραμμή.
Απαντήσεις
Π (-1/2<Χ<1/2)=2/3.
Π(2π /9<Χ< π /2)=1/2.
5.3. ΕΝΑ) Με=1/6, β) Μ(Χ)=3, γ) ρε(Χ)=26/81.
5.4. ΕΝΑ) Με=3/2, β) Μ(Χ)=3/5, γ) ρε(Χ)=12/175.
σι) Μ(Χ)= 3 , ρε(Χ)= 2/9, σ( Χ)= /3.
σι) Μ(Χ)=2 , ρε(Χ)= 3, σ( Χ)= 1,893.
5.7. α) γ = ; σι)
5.8. ΕΝΑ) Με=1/2; σι)
5.9. α) 1/4; β) 0.
5.10. α) 3/5; β) 1.
5.11. ΕΝΑ) Με= 2; σι) Μ(Χ)= 2; σε 1- ln 2 2 ≈ 0,5185.
5.12. ΕΝΑ) Μ(Χ)= π /2 ; β) 1/2
2. ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΑΒΕΒΑΙΟΤΗΤΑΣ ΣΤΗ ΘΕΩΡΙΑ ΛΗΨΗΣ ΑΠΟΦΑΣΕΩΝ
2.2. Πιθανο-στατιστικές μέθοδοι για την περιγραφή αβεβαιοτήτων στη θεωρία αποφάσεων
2.2.4. Τυχαίες μεταβλητές και οι κατανομές τους
Κατανομές τυχαίων μεταβλητών και συναρτήσεις κατανομής. Η κατανομή μιας αριθμητικής τυχαίας μεταβλητής είναι μια συνάρτηση που καθορίζει μοναδικά την πιθανότητα μια τυχαία μεταβλητή να λάβει μια δεδομένη τιμή ή να ανήκει σε κάποιο δεδομένο διάστημα.
Το πρώτο είναι εάν η τυχαία μεταβλητή λάβει έναν πεπερασμένο αριθμό τιμών. Τότε η κατανομή δίνεται από τη συνάρτηση P(X = x),δίνοντας κάθε πιθανή τιμή Χτυχαία μεταβλητή Χη πιθανότητα ότι X = x.
Το δεύτερο είναι εάν η τυχαία μεταβλητή λάβει άπειρες τιμές. Αυτό είναι δυνατό μόνο όταν ο χώρος πιθανότητας στον οποίο ορίζεται η τυχαία μεταβλητή αποτελείται από έναν άπειρο αριθμό στοιχειωδών γεγονότων. Τότε η κατανομή δίνεται από το σύνολο των πιθανοτήτων P(a <
Χ
P(a <
Χ
Αυτή η σχέση δείχνει ότι όπως η κατανομή μπορεί να υπολογιστεί από τη συνάρτηση κατανομής, έτσι, αντίστροφα, η συνάρτηση κατανομής μπορεί να υπολογιστεί από την κατανομή.
Οι συναρτήσεις κατανομής που χρησιμοποιούνται στις πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων και σε άλλες εφαρμοσμένες έρευνες είναι είτε διακριτές είτε συνεχείς, είτε συνδυασμοί τους.
Οι διακριτές συναρτήσεις κατανομής αντιστοιχούν σε διακριτές τυχαίες μεταβλητές που παίρνουν έναν πεπερασμένο αριθμό τιμών ή τιμών από ένα σύνολο των οποίων τα στοιχεία μπορούν να επαναριθμηθούν με φυσικούς αριθμούς (τέτοια σύνολα ονομάζονται μετρήσιμα στα μαθηματικά). Το γράφημα τους μοιάζει με σκάλα (Εικ. 1).
Παράδειγμα 1Αριθμός Χτων ελαττωματικών ειδών στην παρτίδα παίρνει την τιμή 0 με πιθανότητα 0,3, την τιμή 1 με πιθανότητα 0,4, την τιμή 2 με πιθανότητα 0,2 και την τιμή 3 με πιθανότητα 0,1. Γράφημα της συνάρτησης κατανομής μιας τυχαίας μεταβλητής Χφαίνεται στο Σχ.1.
Εικ.1. Γράφημα της συνάρτησης διανομής του αριθμού των ελαττωματικών προϊόντων.
Οι συναρτήσεις συνεχούς διανομής δεν έχουν άλματα. Αυξάνονται μονότονα καθώς αυξάνεται το όρισμα, από 0 για σε 1 για . Οι τυχαίες μεταβλητές με συναρτήσεις συνεχούς κατανομής ονομάζονται συνεχείς.
Οι συναρτήσεις συνεχούς κατανομής που χρησιμοποιούνται στις πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων έχουν παράγωγα. Πρώτο παράγωγο f(x)συναρτήσεις διανομής F(x)ονομάζεται πυκνότητα πιθανότητας,
Η συνάρτηση κατανομής μπορεί να προσδιοριστεί από την πυκνότητα πιθανότητας:

Για οποιαδήποτε συνάρτηση διανομής
και ως εκ τούτου

Οι παρατιθέμενες ιδιότητες των συναρτήσεων κατανομής χρησιμοποιούνται συνεχώς σε πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων. Συγκεκριμένα, η τελευταία ισότητα συνεπάγεται μια συγκεκριμένη μορφή των σταθερών στους τύπους για τις πυκνότητες πιθανότητας που εξετάζονται παρακάτω.
Παράδειγμα 2Η ακόλουθη συνάρτηση διανομής χρησιμοποιείται συχνά:
 (1)
(1)
Οπου έναΚαι σι- κάποιοι αριθμοί ένα . Ας βρούμε την πυκνότητα πιθανότητας αυτής της συνάρτησης κατανομής:

(σε σημεία x = αΚαι x = βπαράγωγο συνάρτησης F(x)δεν υπάρχει).
Μια τυχαία μεταβλητή με συνάρτηση κατανομής (1) ονομάζεται "ομοιόμορφα κατανεμημένη στο διάστημα [ ένα; σι]».
Οι συναρτήσεις μικτής κατανομής εμφανίζονται, ιδιαίτερα, όταν οι παρατηρήσεις σταματούν σε κάποιο σημείο. Για παράδειγμα, κατά την ανάλυση στατιστικών δεδομένων που λαμβάνονται με τη χρήση σχεδίων δοκιμών αξιοπιστίας που προβλέπουν τον τερματισμό των δοκιμών μετά από ένα ορισμένο χρονικό διάστημα. Ή κατά την ανάλυση δεδομένων για τεχνικά προϊόντα που απαιτούσαν επισκευές με εγγύηση.
Παράδειγμα 3Έστω, για παράδειγμα, η διάρκεια ζωής ενός λαμπτήρα ηλεκτρικού φωτός μια τυχαία μεταβλητή με συνάρτηση διανομής F(t),και η δοκιμή διεξάγεται μέχρι να αστοχήσει ο λαμπτήρας, εάν αυτό συμβεί σε λιγότερο από 100 ώρες από την έναρξη της δοκιμής ή μέχρι τη στιγμή t0= 100 ώρες. Αφήνω G(t)- λειτουργία κατανομής του χρόνου λειτουργίας του λαμπτήρα σε καλή κατάσταση σε αυτή τη δοκιμή. Επειτα

Λειτουργία G(t)έχει ένα άλμα σε ένα σημείο t0, αφού η αντίστοιχη τυχαία μεταβλητή παίρνει την τιμή t0με πιθανότητα 1- F(t0)> 0.
Χαρακτηριστικά τυχαίων μεταβλητών.Στις πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων, χρησιμοποιείται ένας αριθμός χαρακτηριστικών τυχαίων μεταβλητών, που εκφράζονται μέσω των συναρτήσεων κατανομής και της πυκνότητας πιθανότητας.
Κατά την περιγραφή της διαφοροποίησης του εισοδήματος, κατά την εύρεση ορίων εμπιστοσύνης για τις παραμέτρους των κατανομών των τυχαίων μεταβλητών και σε πολλές άλλες περιπτώσεις, χρησιμοποιείται μια έννοια όπως "ποσοστό παραγγελίας". R", όπου 0< Π < 1 (обозначается x σελ). Ποσότητα παραγγελίας Rείναι η τιμή μιας τυχαίας μεταβλητής για την οποία η συνάρτηση διανομής παίρνει την τιμή Rή υπάρχει "άλμα" από τιμή μικρότερη από Rμέχρι μια τιμή μεγαλύτερη R(Εικ. 2). Μπορεί να συμβεί αυτή η συνθήκη να ικανοποιείται για όλες τις τιμές του x που ανήκουν σε αυτό το διάστημα (δηλαδή, η συνάρτηση κατανομής είναι σταθερή σε αυτό το διάστημα και ισούται με R). Τότε κάθε τέτοια τιμή ονομάζεται "ποσοστό της τάξης". R».

Εικ.2. Ορισμός ποσοστού x σελΣειρά R.
Για συναρτήσεις συνεχούς κατανομής, κατά κανόνα, υπάρχει ένα μόνο μερίδιο x σελΣειρά R(Εικ. 2), και
F(x p) = p. (2)
Παράδειγμα 4Ας βρούμε την ποσότητα x σελΣειρά Rγια τη συνάρτηση διανομής F(x)από (1).
Στο 0< Π < 1 квантиль x σελβρίσκεται από την εξίσωση
εκείνοι. x σελ = a + p(b – a) = a( 1- p)+bp. Στο Π= 0 οποιαδήποτε Χ < έναείναι η ποσότητα παραγγελίας Π= 0. Ποσότητα παραγγελίας Π= 1 είναι οποιοσδήποτε αριθμός Χ > σι.
Για διακριτές διανομές, κατά κανόνα, δεν υπάρχει x σελικανοποιητική εξίσωση (2). Πιο συγκεκριμένα, εάν η κατανομή μιας τυχαίας μεταβλητής δίνεται στον Πίνακα 1, όπου x 1< x 2 < … < x k , τότε η ισότητα (2), που θεωρείται ως εξίσωση σε σχέση με x σελ, έχει λύσεις μόνο για καξίες Π, και συγκεκριμένα,
p \u003d p 1,
p \u003d p 1 + p 2,
p \u003d p 1 + p 2 + p 3,
p \u003d p 1 + p 2 + ... + p m, 3< m < k,
p \u003d p 1 + p 2 + ... + p k.
Τραπέζι 1.
Κατανομή μιας διακριτής τυχαίας μεταβλητής
|
Αξίες Χτυχαία μεταβλητή Χ |
||||
|
Πιθανότητες P(X=x) |
Για τα αναγραφόμενα κτιμές πιθανότητας Πλύση x σελη εξίσωση (2) δεν είναι μοναδική, δηλαδή,
F(x) = p 1 + p 2 + ... + p m
για όλα Χτέτοια που x m< x < xm+1 .Εκείνοι. x p -οποιοδήποτε αριθμό από το εύρος (x m; x m+1].Για όλους τους άλλους Rαπό το διάστημα (0;1) που δεν περιλαμβάνεται στη λίστα (3), υπάρχει ένα "άλμα" από μια τιμή μικρότερη από Rμέχρι μια τιμή μεγαλύτερη R. Δηλαδή, εάν
p 1 + p 2 + … + p m
Οτι x p \u003d x m + 1.
Η θεωρούμενη ιδιότητα των διακριτών κατανομών δημιουργεί σημαντικές δυσκολίες στον πίνακα και τη χρήση τέτοιων κατανομών, καθώς είναι αδύνατο να διατηρηθούν με ακρίβεια οι τυπικές αριθμητικές τιμές των χαρακτηριστικών κατανομής. Ειδικότερα, αυτό ισχύει για τις κρίσιμες τιμές και τα επίπεδα σημαντικότητας των μη παραμετρικών στατιστικών δοκιμών (βλ. παρακάτω), καθώς οι κατανομές των στατιστικών αυτών των δοκιμών είναι διακριτές.
Το ποσό της παραγγελίας έχει μεγάλη σημασία στη στατιστική. R= Σ. Ονομάζεται διάμεσος (τυχαία μεταβλητή Χή τη συνάρτηση διανομής του F(x))και συμβολίζεται Εγώ (Χ).Στη γεωμετρία, υπάρχει η έννοια της "διάμεσος" - μια ευθεία γραμμή που διέρχεται από την κορυφή ενός τριγώνου και διαιρεί την αντίθετη πλευρά του στο μισό. Στη μαθηματική στατιστική, η διάμεσος διχοτομεί όχι την πλευρά του τριγώνου, αλλά την κατανομή μιας τυχαίας μεταβλητής: ισότητα F(x0,5)= 0,5 σημαίνει ότι η πιθανότητα να φτάσεις στα αριστερά x0,5και η πιθανότητα να γίνει σωστά x0,5(ή απευθείας σε x0,5) είναι ίσα μεταξύ τους και ίσα με S, δηλ.
Π(Χ < Χ 0,5) = Π(Χ > Χ 0,5) = S.
Η διάμεσος υποδηλώνει το «κέντρο» της διανομής. Από τη σκοπιά μιας από τις σύγχρονες έννοιες - της θεωρίας των σταθερών στατιστικών διαδικασιών - η διάμεσος είναι καλύτερο χαρακτηριστικό μιας τυχαίας μεταβλητής από τη μαθηματική προσδοκία. Όταν η επεξεργασία των αποτελεσμάτων της μέτρησης σε μια τακτική κλίμακα (δείτε το κεφάλαιο για τη θεωρία μετρήσεων), μπορεί να χρησιμοποιηθεί η διάμεσος, αλλά η μαθηματική προσδοκία όχι.
Ένα τέτοιο χαρακτηριστικό μιας τυχαίας μεταβλητής ως τρόπος έχει μια σαφή σημασία - την τιμή (ή τις τιμές) μιας τυχαίας μεταβλητής που αντιστοιχεί σε ένα τοπικό μέγιστο της πυκνότητας πιθανότητας για μια συνεχή τυχαία μεταβλητή ή ένα τοπικό μέγιστο της πιθανότητας για μια διακριτή τυχαία μεταβλητός.
Αν x0είναι ο τρόπος μιας τυχαίας μεταβλητής με πυκνότητα f(x),τότε, όπως είναι γνωστό από τον διαφορικό λογισμό, .
Μια τυχαία μεταβλητή μπορεί να έχει πολλούς τρόπους. Έτσι, για ομοιόμορφη κατανομή (1) κάθε σημείο Χτέτοια που ένα< x < b , είναι μόδα. Ωστόσο, αυτό είναι μια εξαίρεση. Οι περισσότερες από τις τυχαίες μεταβλητές που χρησιμοποιούνται στις πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων και σε άλλες εφαρμοσμένες έρευνες έχουν έναν τρόπο. Οι τυχαίες μεταβλητές, οι πυκνότητες, οι κατανομές που έχουν έναν τρόπο ονομάζονται μονοτροπικές.
Η μαθηματική προσδοκία για διακριτές τυχαίες μεταβλητές με πεπερασμένο αριθμό τιμών εξετάζεται στο κεφάλαιο "Γεγονότα και Πιθανότητες". Για μια συνεχή τυχαία μεταβλητή Χαναμενόμενη αξία M(X)ικανοποιεί την ισότητα

που είναι ανάλογο του τύπου (5) από τη δήλωση 2 του κεφαλαίου «Γεγονότα και πιθανότητες».
Παράδειγμα 5Μαθηματική προσδοκία για μια ομοιόμορφα κατανεμημένη τυχαία μεταβλητή Χισοδυναμεί
Για τις τυχαίες μεταβλητές που εξετάζονται σε αυτό το κεφάλαιο, όλες εκείνες οι ιδιότητες των μαθηματικών προσδοκιών και διακυμάνσεων που εξετάστηκαν νωρίτερα για διακριτές τυχαίες μεταβλητές με πεπερασμένο αριθμό τιμών είναι αληθείς. Ωστόσο, δεν παρέχουμε αποδείξεις για αυτές τις ιδιότητες, καθώς απαιτούν εμβάθυνση σε μαθηματικές λεπτότητες, κάτι που δεν είναι απαραίτητο για την κατανόηση και την κατάλληλη εφαρμογή των πιθανοτικών-στατιστικών μεθόδων λήψης αποφάσεων.
Σχόλιο.Σε αυτό το εγχειρίδιο αποφεύγονται σκόπιμα οι μαθηματικές λεπτότητες, οι οποίες συνδέονται, ειδικότερα, με τις έννοιες των μετρήσιμων συνόλων και των μετρήσιμων συναρτήσεων, της -άλγεβρας των γεγονότων κ.λπ. Όσοι επιθυμούν να κατακτήσουν αυτές τις έννοιες θα πρέπει να ανατρέξουν στην εξειδικευμένη βιβλιογραφία, ιδίως στην εγκυκλοπαίδεια.
Καθένα από τα τρία χαρακτηριστικά - μαθηματική προσδοκία, διάμεσος, τρόπος - περιγράφει το «κέντρο» της κατανομής πιθανοτήτων. Η έννοια του «κέντρου» μπορεί να οριστεί με διαφορετικούς τρόπους - εξ ου και τα τρία διαφορετικά χαρακτηριστικά. Ωστόσο, για μια σημαντική κατηγορία κατανομών - συμμετρική μονοτροπική - και τα τρία χαρακτηριστικά συμπίπτουν.
Πυκνότητα κατανομής f(x)είναι η πυκνότητα της συμμετρικής κατανομής, αν υπάρχει αριθμός x 0τέτοια που
![]() . (3)
. (3)
Ισότητα (3) σημαίνει ότι η γραφική παράσταση της συνάρτησης y = f(x)συμμετρικό ως προς μια κατακόρυφη γραμμή που διέρχεται από το κέντρο της συμμετρίας Χ = Χ 0 . Από το (3) προκύπτει ότι η συνάρτηση συμμετρικής κατανομής ικανοποιεί τη σχέση
![]() (4)
(4)
Για μια συμμετρική κατανομή με έναν τρόπο, ο μέσος όρος, η διάμεσος και ο τρόπος είναι ίδιες και ίσες x 0.
Η πιο σημαντική περίπτωση είναι η συμμετρία ως προς το 0, δηλ. x 0= 0. Τότε (3) και (4) γίνονται ισότητες
![]() (6)
(6)
αντίστοιχα. Οι παραπάνω σχέσεις δείχνουν ότι δεν υπάρχει ανάγκη να συνοψιστούν συμμετρικές κατανομές για όλους Χ, αρκεί να υπάρχουν τραπέζια για Χ > x0.
Σημειώνουμε μια ακόμη ιδιότητα των συμμετρικών κατανομών, η οποία χρησιμοποιείται συνεχώς σε πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων και σε άλλες εφαρμοσμένες έρευνες. Για συνάρτηση συνεχούς διανομής
Ρ(|Χ| < α) = Ρ(-α < Χ < α) = F(a) – F(-a),
Οπου φάείναι η συνάρτηση κατανομής της τυχαίας μεταβλητής Χ. Αν η συνάρτηση κατανομής φάείναι συμμετρικό ως προς το 0, δηλ. Ο τύπος (6) ισχύει για αυτό, λοιπόν
Ρ(|Χ| < α) = 2F(a) - 1.
Μια άλλη διατύπωση της υπό εξέταση δήλωσης χρησιμοποιείται συχνά: αν
![]() .
.
Αν και είναι ποσοστά της τάξης και, αντίστοιχα (βλ. (2)) μιας συνάρτησης κατανομής συμμετρικά ως προς το 0, τότε από το (6) προκύπτει ότι
Από τα χαρακτηριστικά της θέσης - μαθηματική προσδοκία, διάμεσοι, τρόποι - ας προχωρήσουμε στα χαρακτηριστικά της εξάπλωσης μιας τυχαίας μεταβλητής Χ: διακύμανση , τυπική απόκλιση και συντελεστής διακύμανσης v. Ο ορισμός και οι ιδιότητες της διακύμανσης για διακριτές τυχαίες μεταβλητές εξετάστηκαν στο προηγούμενο κεφάλαιο. Για συνεχείς τυχαίες μεταβλητές
Η τυπική απόκλιση είναι η μη αρνητική τιμή της τετραγωνικής ρίζας της διακύμανσης:
Ο συντελεστής διακύμανσης είναι ο λόγος της τυπικής απόκλισης προς τη μαθηματική προσδοκία:
Ο συντελεστής διακύμανσης εφαρμόζεται όταν Μ(Χ)> 0. Μετρά το spread σε σχετικές μονάδες, ενώ η τυπική απόκλιση είναι σε απόλυτες μονάδες.
Παράδειγμα 6Για μια ομοιόμορφα κατανεμημένη τυχαία μεταβλητή Χβρείτε τη διακύμανση, την τυπική απόκλιση και τον συντελεστή διακύμανσης. Η διασπορά είναι:

Η αντικατάσταση μεταβλητής καθιστά δυνατή τη σύνταξη:
Οπου ντο = (σι – ένα)/ 2. Επομένως, η τυπική απόκλιση είναι ίση με και ο συντελεστής διακύμανσης είναι:
Για κάθε τυχαία μεταβλητή Χκαθορίστε τρεις ακόμη ποσότητες - κεντραρισμένες Υ, κανονικοποιημένη Vκαι δεδομένο U. Κεντροποιημένη τυχαία μεταβλητή Υείναι η διαφορά μεταξύ της δεδομένης τυχαίας μεταβλητής Χκαι τη μαθηματική του προσδοκία M(X),εκείνοι. Υ = Χ - Μ(Χ).Μαθηματική προσδοκία μιας κεντραρισμένης τυχαίας μεταβλητής Υισούται με 0 και η διακύμανση είναι η διακύμανση της δεδομένης τυχαίας μεταβλητής: Μ(Υ) = 0, ρε(Υ) = ρε(Χ). συνάρτηση διανομής F Y(Χ) κεντραρισμένη τυχαία μεταβλητή Υπου σχετίζονται με τη συνάρτηση διανομής φά(Χ) αρχική τυχαία μεταβλητή Χαναλογία:
F Y(Χ) = φά(Χ + Μ(Χ)).
Για τις πυκνότητες αυτών των τυχαίων μεταβλητών, η ισότητα
στ Υ(Χ) = φά(Χ + Μ(Χ)).
Κανονοποιημένη τυχαία μεταβλητή Vείναι ο λόγος αυτής της τυχαίας μεταβλητής Χστην τυπική του απόκλιση, δηλ. . Μαθηματική προσδοκία και διακύμανση μιας κανονικοποιημένης τυχαίας μεταβλητής Vεκφράζεται μέσα από χαρακτηριστικά ΧΕτσι:
![]() ,
,
Οπου vείναι ο συντελεστής διακύμανσης της αρχικής τυχαίας μεταβλητής Χ. Για τη συνάρτηση διανομής F V(Χ) και πυκνότητα f V(Χ) κανονικοποιημένη τυχαία μεταβλητή Vέχουμε:
Οπου φά(Χ) είναι η συνάρτηση κατανομής της αρχικής τυχαίας μεταβλητής Χ, ΕΝΑ φά(Χ) είναι η πυκνότητα πιθανοτήτων του.
Μειωμένη τυχαία μεταβλητή Uείναι μια κεντραρισμένη και κανονικοποιημένη τυχαία μεταβλητή:
![]() .
.
Για μειωμένη τυχαία μεταβλητή
Οι κανονικοποιημένες, κεντρικές και μειωμένες τυχαίες μεταβλητές χρησιμοποιούνται συνεχώς τόσο στη θεωρητική έρευνα όσο και σε αλγόριθμους, προϊόντα λογισμικού, κανονιστική και τεχνική και διδακτική και μεθοδολογική τεκμηρίωση. Ειδικότερα, γιατί οι ισότητες ![]() καθιστούν δυνατή την απλοποίηση της τεκμηρίωσης μεθόδων, διατυπώσεων θεωρημάτων και τύπων υπολογισμού.
καθιστούν δυνατή την απλοποίηση της τεκμηρίωσης μεθόδων, διατυπώσεων θεωρημάτων και τύπων υπολογισμού.
Χρησιμοποιούνται μετασχηματισμοί τυχαίων μεταβλητών και πιο γενικό σχέδιο. Οπότε αν Υ = τσεκούρι + σι, Οπου έναΚαι σιείναι κάποιοι αριθμοί, λοιπόν
Παράδειγμα 7Αν τότε Υείναι η μειωμένη τυχαία μεταβλητή και οι τύποι (8) μετατρέπονται σε τύπους (7).
Με κάθε τυχαία μεταβλητή Χμπορείτε να συνδέσετε πολλές τυχαίες μεταβλητές Υδίνεται από τον τύπο Υ = τσεκούρι + σισε διάφορα ένα> 0 και σι. Αυτό το σύνολο ονομάζεται οικογένεια μετατόπισης κλίμακας, που δημιουργείται από μια τυχαία μεταβλητή Χ. Λειτουργίες διανομής F Y(Χ) αποτελούν μια οικογένεια διανομών μετατόπισης κλίμακας που δημιουργείται από τη συνάρτηση διανομής φά(Χ). Αντί Υ = τσεκούρι + σισυχνά χρησιμοποιούμενος συμβολισμός
![]()
Αριθμός Μεονομάζεται παράμετρος shift και αριθμός ρε- παράμετρος κλίμακας. Ο τύπος (9) δείχνει ότι Χ- το αποτέλεσμα της μέτρησης μιας ορισμένης ποσότητας - μπαίνει Στο- το αποτέλεσμα της μέτρησης της ίδιας τιμής, εάν η αρχή της μέτρησης μετακινηθεί στο σημείο Με, και στη συνέχεια χρησιμοποιήστε τη νέα μονάδα μέτρησης, στο ρεφορές μεγαλύτερη από την παλιά.
Για την οικογένεια μετατόπισης κλίμακας (9), η κατανομή X ονομάζεται τυπική. Στις πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων και σε άλλες εφαρμοσμένες έρευνες, χρησιμοποιούνται η τυπική κανονική κατανομή, η τυπική κατανομή Weibull-Gnedenko, η τυπική κατανομή γάμμα κ.λπ. (βλ. παρακάτω).
Χρησιμοποιούνται επίσης άλλοι μετασχηματισμοί τυχαίων μεταβλητών. Για παράδειγμα, για μια θετική τυχαία μεταβλητή Χσκεφτείτε Υ= κούτσουρο Χ, όπου lg Χείναι ο δεκαδικός λογάριθμος του αριθμού Χ. Αλυσίδα ισοτήτων
F Y (x) = P( lg Χ< x) = P(X < 10x) = F( 10Χ)
σχετίζεται με συναρτήσεις διανομής ΧΚαι Υ.
Κατά την επεξεργασία δεδομένων, χρησιμοποιούνται τέτοια χαρακτηριστικά μιας τυχαίας μεταβλητής Χσαν στιγμές τάξης q, δηλ. μαθηματικές προσδοκίες μιας τυχαίας μεταβλητής X q, q= 1, 2, … Έτσι, η ίδια η μαθηματική προσδοκία είναι μια στιγμή της τάξης 1. Για μια διακριτή τυχαία μεταβλητή, η στιγμή της τάξης qμπορεί να υπολογιστεί ως
![]()
Για μια συνεχή τυχαία μεταβλητή

Στιγμές τάξης qκαλούνται επίσης οι αρχικές στιγμές της παραγγελίας q, σε αντίθεση με τα σχετικά χαρακτηριστικά - τις κεντρικές στιγμές της παραγγελίας q, δίνεται από τον τύπο
Έτσι, η διασπορά είναι μια κεντρική στιγμή της τάξης 2.
Κανονική κατανομή και θεώρημα κεντρικού ορίου.Στις πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων, μιλάμε συχνά για κανονική κατανομή. Μερικές φορές προσπαθούν να το χρησιμοποιήσουν για να μοντελοποιήσουν την κατανομή των αρχικών δεδομένων (αυτές οι προσπάθειες δεν δικαιολογούνται πάντα - βλέπε παρακάτω). Το πιο σημαντικό, πολλές μέθοδοι επεξεργασίας δεδομένων βασίζονται στο γεγονός ότι οι υπολογισμένες τιμές έχουν κατανομές κοντά στο κανονικό.
Αφήνω Χ 1 , Χ 2 ,…, X n Μ(X i) = Μκαι διασπορές ρε(X i) = , Εγώ= 1, 2,…, n,… Όπως προκύπτει από τα αποτελέσματα του προηγούμενου κεφαλαίου,
Θεωρήστε τη μειωμένη τυχαία μεταβλητή U nγια το άθροισμα ![]() , και συγκεκριμένα,
, και συγκεκριμένα,
![]()
Όπως προκύπτει από τους τύπους (7), Μ(U n) = 0, ρε(U n) = 1.
(για πανομοιότυπα κατανεμημένους όρους). Αφήνω Χ 1 , Χ 2 ,…, X n, … είναι ανεξάρτητες πανομοιότυπα κατανεμημένες τυχαίες μεταβλητές με μαθηματικές προσδοκίες Μ(X i) = Μκαι διασπορές ρε(X i) = , Εγώ= 1, 2,…, n,… Τότε για οποιοδήποτε x υπάρχει ένα όριο

Οπου F(x)– λειτουργία του προτύπου κανονική κατανομή.
Περισσότερα για τη λειτουργία F(x) -παρακάτω (διαγράφει "fi από x", γιατί φά- Ελληνικό κεφαλαίο γράμμα «φι»).
Το κεντρικό οριακό θεώρημα (CLT) πήρε το όνομά του από το γεγονός ότι είναι το κεντρικό, πιο συχνά χρησιμοποιούμενο μαθηματικό αποτέλεσμα της θεωρίας πιθανοτήτων και της μαθηματικής στατιστικής. Η ιστορία του CLT διαρκεί περίπου 200 χρόνια - από το 1730, όταν ο Άγγλος μαθηματικός A. De Moivre (1667-1754) δημοσίευσε το πρώτο αποτέλεσμα που σχετίζεται με το CLT (βλ. παρακάτω για το θεώρημα Moivre-Laplace), μέχρι τη δεκαετία του 20-30 του εικοστού αιώνα, όταν ο Finn J.W. Lindeberg, Γάλλος Paul Levy (1886-1971), Γιουγκοσλάβος V. Feller (1906-1970), Ρώσος A.Ya. Ο Khinchin (1894-1959) και άλλοι επιστήμονες απέκτησαν τις απαραίτητες και επαρκείς προϋποθέσεις για την εγκυρότητα του κλασικού κεντρικού οριακού θεωρήματος.
Η ανάπτυξη του υπό εξέταση θέματος δεν σταμάτησε καθόλου εκεί - μελέτησαν τυχαίες μεταβλητές που δεν έχουν διασπορά, δηλ. αυτοί για τους οποίους

(ακαδημαϊκός B.V. Gnedenko και άλλοι), η κατάσταση όταν συνοψίζονται τυχαίες μεταβλητές (ακριβέστερα, τυχαία στοιχεία) πιο σύνθετης φύσης από τους αριθμούς (ακαδημαϊκοί Yu.V. Prokhorov, A.A. Borovkov και οι συνεργάτες τους) κ.λπ. .d.
συνάρτηση διανομής F(x)δίνεται από την ισότητα
![]() ,
,
πού είναι η πυκνότητα της τυπικής κανονικής κατανομής, η οποία έχει μια μάλλον περίπλοκη έκφραση:
![]() .
.
Εδώ \u003d 3.1415925 ... είναι ένας αριθμός γνωστός στη γεωμετρία, ίσος με τον λόγο της περιφέρειας προς τη διάμετρο, μι\u003d 2.718281828 ... - η βάση των φυσικών λογαρίθμων (για να θυμάστε αυτόν τον αριθμό, σημειώστε ότι το 1828 είναι το έτος γέννησης του συγγραφέα Λέων Τολστόι). Όπως είναι γνωστό από τη μαθηματική ανάλυση,

Κατά την επεξεργασία των αποτελεσμάτων των παρατηρήσεων, η συνάρτηση κανονικής κατανομής δεν υπολογίζεται σύμφωνα με τους παραπάνω τύπους, αλλά βρίσκεται χρησιμοποιώντας ειδικούς πίνακες ή προγράμματα υπολογιστή. Οι καλύτεροι στα ρωσικά «Πίνακες Μαθηματικής Στατιστικής» συντάχθηκαν από Αντεπιστέλλοντα Μέλη της Ακαδημίας Επιστημών της ΕΣΣΔ L.N. Bolshev και N.V. Smirnov.
Η μορφή της πυκνότητας της τυπικής κανονικής κατανομής προκύπτει από τη μαθηματική θεωρία, την οποία δεν μπορούμε να εξετάσουμε εδώ, καθώς και την απόδειξη του CLT.
Για παράδειγμα, παρουσιάζουμε μικρούς πίνακες της συνάρτησης κατανομής F(x)(Πίνακας 2) και τα ποσοστά του (Πίνακας 3). Λειτουργία F(x)είναι συμμετρικό ως προς το 0, το οποίο αντικατοπτρίζεται στους Πίνακες 2-3.
Πίνακας 2.
Συνάρτηση της τυπικής κανονικής κατανομής.
Αν η τυχαία μεταβλητή Χέχει συνάρτηση διανομής F(x),Οτι M(X) = 0, ρε(Χ) = 1. Αυτή η δήλωση αποδεικνύεται στη θεωρία πιθανοτήτων με βάση τη μορφή της πυκνότητας πιθανότητας . Συμφωνεί με παρόμοια δήλωση για τα χαρακτηριστικά της μειωμένης τυχαίας μεταβλητής U n, το οποίο είναι απολύτως φυσικό, αφού το CLT αναφέρει ότι με άπειρη αύξηση του αριθμού των όρων, η συνάρτηση κατανομής U nτείνει στην τυπική συνάρτηση κανονικής κατανομής F(x),και για οποιαδήποτε Χ.
Πίνακας 3
Ποσότητα της τυπικής κανονικής κατανομής.
|
Ποσότητα παραγγελίας R |
Ποσότητα παραγγελίας R |
||
Ας εισαγάγουμε την έννοια μιας οικογένειας κανονικών κατανομών. Εξ ορισμού, μια κανονική κατανομή είναι η κατανομή μιας τυχαίας μεταβλητής Χ, για την οποία η κατανομή της μειωμένης τυχαίας μεταβλητής είναι F(x).Όπως προκύπτει από τις γενικές ιδιότητες των οικογενειών κατανομών μετατόπισης κλίμακας (βλ. παραπάνω), η κανονική κατανομή είναι η κατανομή μιας τυχαίας μεταβλητής
Οπου Χείναι μια τυχαία μεταβλητή με κατανομή F(X),και Μ = Μ(Υ), = ρε(Υ). Κανονική κατανομή με παραμέτρους μετατόπισης Μκαι συνήθως υποδηλώνεται κλίμακα Ν(Μ, ) (μερικές φορές η σημειογραφία Ν(Μ, ) ).
Όπως προκύπτει από το (8), η πυκνότητα πιθανότητας της κανονικής κατανομής Ν(Μ, ) Υπάρχει

Οι κανονικές κατανομές σχηματίζουν μια οικογένεια μετατόπισης κλίμακας. Σε αυτή την περίπτωση, η παράμετρος κλίμακας είναι ρε= 1/ και η παράμετρος shift ντο = - Μ/ .
Για τις κεντρικές στιγμές της τρίτης και τέταρτης τάξης της κανονικής κατανομής, οι ισότητες είναι αληθείς
![]()
Αυτές οι ισότητες αποτελούν τη βάση των κλασικών μεθόδων ελέγχου ότι τα αποτελέσματα των παρατηρήσεων ακολουθούν μια κανονική κατανομή. Προς το παρόν, η κανονικότητα συνήθως συνιστάται να ελέγχεται με το κριτήριο W Shapiro - Wilka. Το πρόβλημα του ελέγχου κανονικότητας συζητείται παρακάτω.
Αν τυχαίες μεταβλητές Χ 1Και Χ 2έχουν συναρτήσεις διανομής Ν(Μ 1
, 1
)
Και Ν(Μ 2
, 2
)
αντίστοιχα, λοιπόν Χ 1+ Χ 2έχει διανομή ![]() Επομένως, εάν οι τυχαίες μεταβλητές Χ 1
,
Χ 2
,…,
X n Ν(Μ, )
, τότε ο αριθμητικός τους μέσος όρος
Επομένως, εάν οι τυχαίες μεταβλητές Χ 1
,
Χ 2
,…,
X n Ν(Μ, )
, τότε ο αριθμητικός τους μέσος όρος
![]()
έχει διανομή Ν(Μ, ) . Αυτές οι ιδιότητες της κανονικής κατανομής χρησιμοποιούνται συνεχώς σε διάφορες πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων, ειδικότερα στον στατιστικό έλεγχο τεχνολογικών διεργασιών και στον στατιστικό έλεγχο αποδοχής από ένα ποσοτικό χαρακτηριστικό.
Η κανονική κατανομή ορίζει τρεις κατανομές που χρησιμοποιούνται πλέον συνήθως στη στατιστική επεξεργασία δεδομένων.
Κατανομή (χι - τετράγωνο) - κατανομή μιας τυχαίας μεταβλητής
όπου τυχαίες μεταβλητές Χ 1 , Χ 2 ,…, X nείναι ανεξάρτητα και έχουν την ίδια κατανομή Ν(0,1). Σε αυτή την περίπτωση, ο αριθμός των όρων, δηλ. n, ονομάζεται «αριθμός βαθμών ελευθερίας» της κατανομής χι-τετράγωνο.
Διανομή t Student είναι η κατανομή μιας τυχαίας μεταβλητής
όπου τυχαίες μεταβλητές UΚαι Χανεξάρτητος, Uέχει τυπική κανονική κατανομή Ν(0,1) και Χ– κατανομή chi – τετράγωνο με nβαθμοί ελευθερίας. Εν nονομάζεται «αριθμός βαθμών ελευθερίας» της κατανομής του Μαθητή. Αυτή η διανομή εισήχθη το 1908 από τον Άγγλο στατιστικολόγο W. Gosset, ο οποίος εργαζόταν σε ένα εργοστάσιο μπύρας. Οι πιθανοτικές-στατιστικές μέθοδοι χρησιμοποιήθηκαν για τη λήψη οικονομικών και τεχνικών αποφάσεων σε αυτό το εργοστάσιο, έτσι η διοίκηση του απαγόρευσε στον V. Gosset να δημοσιεύει επιστημονικά άρθρα με το όνομά του. Με αυτόν τον τρόπο προστατεύτηκε ένα εμπορικό μυστικό, «τεχνογνωσία» με τη μορφή πιθανοτικών-στατιστικών μεθόδων που ανέπτυξε ο W. Gosset. Ωστόσο, μπόρεσε να δημοσιεύσει με το ψευδώνυμο «Φοιτητής». Η ιστορία του Gosset - Student δείχνει ότι για άλλα εκατό χρόνια η μεγάλη οικονομική αποτελεσματικότητα των πιθανοτικών-στατιστικών μεθόδων λήψης αποφάσεων ήταν εμφανής στους Βρετανούς μάνατζερ.
Η κατανομή Fisher είναι η κατανομή μιας τυχαίας μεταβλητής
όπου τυχαίες μεταβλητές Χ 1Και Χ 2είναι ανεξάρτητες και έχουν κατανομές chi - το τετράγωνο με τον αριθμό των βαθμών ελευθερίας κ 1 Και κ 2 αντίστοιχα. Παράλληλα, ένα ζευγάρι (κ 1 , κ 2 ) είναι ένα ζεύγος «αριθμών βαθμών ελευθερίας» της κατανομής Fisher, δηλαδή, κ 1 είναι ο αριθμός των βαθμών ελευθερίας του αριθμητή, και κ 2 είναι ο αριθμός των βαθμών ελευθερίας του παρονομαστή. Η κατανομή της τυχαίας μεταβλητής F πήρε το όνομά του από τον σπουδαίο Άγγλο στατιστικολόγο R. Fisher (1890-1962), ο οποίος τη χρησιμοποίησε ενεργά στο έργο του.
Εκφράσεις για τις συναρτήσεις κατανομής των chi - Square, Student και Fisher, οι πυκνότητες και τα χαρακτηριστικά τους, καθώς και πίνακες μπορούν να βρεθούν στην ειδική βιβλιογραφία (βλ., για παράδειγμα,).
Όπως έχει ήδη σημειωθεί, οι κανονικές κατανομές χρησιμοποιούνται συχνά σε πιθανοτικά μοντέλα σε διάφορα εφαρμοσμένα πεδία. Γιατί αυτή η οικογένεια διανομών δύο παραμέτρων είναι τόσο διαδεδομένη; Διευκρινίζεται από το παρακάτω θεώρημα.
Κεντρικό οριακό θεώρημα(για διαφορετικούς όρους). Αφήνω Χ 1 , Χ 2 ,…, X n,… είναι ανεξάρτητες τυχαίες μεταβλητές με μαθηματικές προσδοκίες Μ(Χ 1 ), Μ(Χ 2 ),…, Μ(Χιδ), … και διασπορές ρε(Χ 1 ), ρε(Χ 2 ),…, ρε(Χιδ), … αντίστοιχα. Αφήνω
Στη συνέχεια, υπό την ισχύ ορισμένων προϋποθέσεων που διασφαλίζουν τη μικρότητα της συμβολής οποιουδήποτε από τους όρους σε U n,
![]()
Για οποιονδηποτε Χ.
Οι εν λόγω προϋποθέσεις δεν θα διατυπωθούν εδώ. Μπορούν να βρεθούν στην εξειδικευμένη βιβλιογραφία (βλ., για παράδειγμα,). «Η αποσαφήνιση των συνθηκών υπό τις οποίες λειτουργεί η CPT είναι η αξία των εξαιρετικών Ρώσων επιστημόνων A.A. Markov (1857-1922) και, ειδικότερα, του A.M. Lyapunov (1857-1918)».
Το θεώρημα του κεντρικού ορίου δείχνει ότι στην περίπτωση που το αποτέλεσμα της μέτρησης (παρατήρηση) διαμορφώνεται υπό την επίδραση πολλών λόγων, καθένας από αυτούς συνεισφέρει μόνο σε μικρή συνεισφορά, και το σωρευτικό αποτέλεσμα καθορίζεται από προσθετικά, δηλ. με πρόσθεση, τότε η κατανομή του αποτελέσματος της μέτρησης (παρατήρησης) είναι κοντά στο κανονικό.
Μερικές φορές πιστεύεται ότι για να είναι η κατανομή κανονική αρκεί το αποτέλεσμα της μέτρησης (παρατήρηση) Χσχηματίζεται υπό την επίδραση πολλών αιτιών, καθεμία από τις οποίες έχει ένα μικρό αποτέλεσμα. Αυτό είναι λάθος. Αυτό που έχει σημασία είναι πώς λειτουργούν αυτές οι αιτίες. Αν είναι πρόσθετο, τότε Χέχει περίπου κανονική κατανομή. Αν πολλαπλασιαστικά(δηλαδή πολλαπλασιάζονται, δεν προστίθενται οι ενέργειες των επιμέρους αιτιών), μετά η κατανομή Χόχι κοντά στο κανονικό, αλλά στο λεγόμενο. λογαριθμικά κανονική, δηλ. Δεν Χ, και το lg X έχει περίπου κανονική κατανομή. Εάν δεν υπάρχουν λόγοι να πιστεύουμε ότι ένας από αυτούς τους δύο μηχανισμούς για τον σχηματισμό του τελικού αποτελέσματος (ή κάποιος άλλος καλά καθορισμένος μηχανισμός) λειτουργεί, τότε σχετικά με τη διανομή Χτίποτα συγκεκριμένο δεν μπορεί να ειπωθεί.
Από όσα ειπώθηκαν, προκύπτει ότι σε ένα συγκεκριμένο εφαρμοσμένο πρόβλημα, η κανονικότητα των αποτελεσμάτων των μετρήσεων (παρατηρήσεις), κατά κανόνα, δεν μπορεί να διαπιστωθεί από γενικές εκτιμήσεις, θα πρέπει να ελέγχεται χρησιμοποιώντας στατιστικά κριτήρια. Ή χρησιμοποιήστε μη παραμετρικές στατιστικές μεθόδους που δεν βασίζονται σε υποθέσεις σχετικά με τις συναρτήσεις κατανομής των αποτελεσμάτων μέτρησης (παρατηρήσεις) που ανήκουν σε μια ή την άλλη παραμετρική οικογένεια.
Συνεχείς κατανομές που χρησιμοποιούνται σε πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων.Εκτός από την οικογένεια κανονικών κατανομών μετατόπισης κλίμακας, χρησιμοποιούνται ευρέως και διάφορες άλλες οικογένειες κατανομών - λογαριθμικά κανονικές, εκθετικές, Weibull-Gnedenko, κατανομές γάμμα. Ας ρίξουμε μια ματιά σε αυτές τις οικογένειες.
Τυχαία τιμή Χέχει λογαριθμική κανονική κατανομή εάν η τυχαία μεταβλητή Υ= κούτσουρο Χέχει κανονική κατανομή. Επειτα Ζ=ln Χ = 2,3026…Υέχει επίσης κανονική κατανομή Ν(ένα 1 ,σ 1), όπου ln Χ- φυσικός λογάριθμος Χ. Η πυκνότητα της λογαριθμικής-κανονικής κατανομής είναι:

Από το κεντρικό οριακό θεώρημα προκύπτει ότι το γινόμενο Χ = Χ 1 Χ 2 … X nανεξάρτητες θετικές τυχαίες μεταβλητές X i, Εγώ = 1, 2,…, n, γενικά nμπορεί να προσεγγιστεί με μια λογαριθμική κανονική κατανομή. Ειδικότερα, το πολλαπλασιαστικό μοντέλο του σχηματισμού μισθών ή εισοδήματος οδηγεί στη σύσταση για προσέγγιση των κατανομών μισθών και εισοδημάτων με λογαριθμικά κανονικούς νόμους. Για τη Ρωσία, αυτή η σύσταση αποδείχθηκε δικαιολογημένη - τα στατιστικά στοιχεία το επιβεβαιώνουν.
Υπάρχουν άλλα πιθανολογικά μοντέλα που οδηγούν στον νόμο λογαριθμικού κανονικού. Ένα κλασικό παράδειγμα τέτοιου μοντέλου δίνεται από τον Α.Ν. Οι σφαιρόμυλοι έχουν κανονική κατανομή.
Ας περάσουμε σε μια άλλη οικογένεια κατανομών, που χρησιμοποιείται ευρέως σε διάφορες πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων και άλλες εφαρμοσμένες έρευνες, την οικογένεια των εκθετικών κατανομών. Ας ξεκινήσουμε με ένα πιθανολογικό μοντέλο που οδηγεί σε τέτοιες κατανομές. Για να το κάνετε αυτό, σκεφτείτε τη «ροή γεγονότων», δηλ. μια σειρά γεγονότων που συμβαίνουν το ένα μετά το άλλο σε κάποια χρονική στιγμή. Παραδείγματα είναι: ροή κλήσεων στο τηλεφωνικό κέντρο. η ροή αστοχιών εξοπλισμού στην τεχνολογική αλυσίδα· ροή αστοχιών του προϊόντος κατά τη διάρκεια της δοκιμής του προϊόντος. τη ροή των αιτημάτων των πελατών προς το υποκατάστημα της τράπεζας· η ροή των αγοραστών που υποβάλλουν αίτηση για αγαθά και υπηρεσίες κ.λπ. Στη θεωρία των ροών γεγονότων, ισχύει ένα θεώρημα παρόμοιο με το θεώρημα του κεντρικού ορίου, αλλά δεν ασχολείται με το άθροισμα τυχαίων μεταβλητών, αλλά με το άθροισμα των ροών γεγονότων. Θεωρούμε μια συνολική ροή που αποτελείται από μεγάλο αριθμό ανεξάρτητων ροών, καμία από τις οποίες δεν έχει κυρίαρχη επίδραση στη συνολική ροή. Για παράδειγμα, η ροή των κλήσεων που φτάνουν στο τηλεφωνικό κέντρο αποτελείται από μεγάλο αριθμό ανεξάρτητων ροών κλήσεων που προέρχονται από μεμονωμένους συνδρομητές. Αποδεικνύεται ότι στην περίπτωση που τα χαρακτηριστικά των ροών δεν εξαρτώνται από το χρόνο, η συνολική ροή περιγράφεται πλήρως από έναν αριθμό - την ένταση της ροής. Για τη συνολική ροή, θεωρήστε μια τυχαία μεταβλητή Χ- το μήκος του χρονικού διαστήματος μεταξύ διαδοχικών γεγονότων. Η συνάρτηση διανομής του έχει τη μορφή
 (10)
(10)
Αυτή η κατανομή ονομάζεται εκθετική κατανομή επειδή Ο τύπος (10) περιλαμβάνει την εκθετική συνάρτηση μι -λ Χ. Η τιμή 1/λ είναι παράμετρος κλίμακας. Μερικές φορές εισάγεται και μια παράμετρος shift Με, εκθετική είναι η κατανομή μιας τυχαίας μεταβλητής Χ + γ, όπου η διανομή Χδίνεται από τον τύπο (10).
Οι εκθετικές κατανομές αποτελούν ειδική περίπτωση των λεγόμενων. Διανομές Weibull - Gnedenko. Ονομάζονται από τον μηχανικό W. Weibull, ο οποίος εισήγαγε αυτές τις κατανομές στην πρακτική της ανάλυσης των αποτελεσμάτων των δοκιμών κόπωσης, και τον μαθηματικό B.V. Gnedenko (1912-1995), ο οποίος έλαβε τέτοιες κατανομές ως περιοριστικές κατά τη μελέτη του μέγιστου του τεστ Αποτελέσματα. Αφήνω Χ- μια τυχαία μεταβλητή που χαρακτηρίζει τη διάρκεια λειτουργίας ενός προϊόντος, σύνθετου συστήματος, στοιχείου (δηλ. πόρος, χρόνος λειτουργίας έως την οριακή κατάσταση κ.λπ.), τη διάρκεια της λειτουργίας μιας επιχείρησης ή τη ζωή ενός ζωντανού όντος, και τα λοιπά. Το ποσοστό αποτυχίας παίζει σημαντικό ρόλο
![]() (11)
(11)
Οπου φά(Χ) Και φά(Χ) - συνάρτηση κατανομής και πυκνότητα τυχαίας μεταβλητής Χ.
Ας περιγράψουμε την τυπική συμπεριφορά του ποσοστού αποτυχίας. Ολόκληρο το χρονικό διάστημα μπορεί να χωριστεί σε τρεις περιόδους. Στο πρώτο από αυτά, η συνάρτηση λ(x)έχει υψηλές τιμές και σαφή τάση μείωσης (τις περισσότερες φορές μειώνεται μονότονα). Αυτό μπορεί να εξηγηθεί από την παρουσία στην υπό εξέταση παρτίδα μονάδων προϊόντος με εμφανή και λανθάνοντα ελαττώματα, τα οποία οδηγούν σε σχετικά γρήγορη αστοχία αυτών των μονάδων προϊόντος. Η πρώτη περίοδος ονομάζεται περίοδος «διάρρηξης» (ή «διάσπασης»). Αυτό καλύπτεται συνήθως από την περίοδο εγγύησης.
Έπειτα έρχεται η περίοδος κανονικής λειτουργίας, που χαρακτηρίζεται από ένα περίπου σταθερό και σχετικά χαμηλό ποσοστό αστοχίας. Η φύση των αστοχιών κατά τη διάρκεια αυτής της περιόδου είναι αιφνίδιας φύσης (ατυχήματα, σφάλματα του προσωπικού λειτουργίας κ.λπ.) και δεν εξαρτάται από τη διάρκεια λειτουργίας μιας μονάδας προϊόντος.
Τέλος, η τελευταία περίοδος λειτουργίας είναι η περίοδος γήρανσης και φθοράς. Η φύση των αστοχιών κατά τη διάρκεια αυτής της περιόδου είναι σε μη αναστρέψιμες φυσικές, μηχανικές και χημικές αλλαγές στα υλικά, που οδηγούν σε προοδευτική υποβάθμιση της ποιότητας μιας μονάδας παραγωγής και τελική αστοχία της.
Κάθε περίοδος έχει τον δικό της τύπο λειτουργίας λ(x). Εξετάστε την κατηγορία των εξαρτήσεων ισχύος
λ(х) = λ0bxb -1 , (12)
Οπου λ 0 > 0 και σι> 0 - ορισμένες αριθμητικές παράμετροι. Αξίες σι < 1, σι= 0 και σι> 1 αντιστοιχεί στον τύπο του ποσοστού αστοχίας κατά τις περιόδους λειτουργίας, κανονικής λειτουργίας και γήρανσης, αντίστοιχα.
Σχέση (11) για ένα δεδομένο ποσοστό αστοχίας λ(x)- διαφορική εξίσωση ως προς τη συνάρτηση φά(Χ). Από τη θεωρία διαφορικές εξισώσειςακολουθεί ότι
 (13)
(13)
Αντικαθιστώντας το (12) στο (13), παίρνουμε αυτό
 (14)
(14)
Η κατανομή που δίνεται από τον τύπο (14) ονομάζεται κατανομή Weibull - Gnedenko. Επειδή η
τότε από τον τύπο (14) προκύπτει ότι η ποσότητα ΕΝΑ, που δίνεται από τον τύπο (15), είναι μια παράμετρος κλιμάκωσης. Μερικές φορές εισάγεται και μια παράμετρος μετατόπισης, π.χ. Καλούνται οι συναρτήσεις διανομής Weibull - Gnedenko φά(Χ - ντο), Οπου φά(Χ) δίνεται από τον τύπο (14) για μερικά λ 0 και σι.
Η πυκνότητα της κατανομής Weibull - Gnedenko έχει τη μορφή
 (16)
(16)
Οπου ένα> 0 - παράμετρος κλίμακας, σι> 0 - παράμετρος φόρμας, Με- παράμετρος μετατόπισης. Σε αυτή την περίπτωση, η παράμετρος ΕΝΑαπό τον τύπο (16) σχετίζεται με την παράμετρο λ 0 από τον τύπο (14) με την αναλογία που υποδεικνύεται στον τύπο (15).
Η εκθετική κατανομή είναι μια πολύ ειδική περίπτωση της κατανομής Weibull - Gnedenko, που αντιστοιχεί στην τιμή της παραμέτρου σχήματος σι = 1.
Η κατανομή Weibull - Gnedenko χρησιμοποιείται επίσης στην κατασκευή πιθανοτικών μοντέλων καταστάσεων στις οποίες η συμπεριφορά ενός αντικειμένου καθορίζεται από τον «πιο αδύναμο κρίκο». Υπονοείται μια αναλογία με μια αλυσίδα, η ασφάλεια της οποίας καθορίζεται από τον κρίκο που έχει τη χαμηλότερη αντοχή. Με άλλα λόγια, ας Χ 1 , Χ 2 ,…, X nείναι ανεξάρτητες πανομοιότυπα κατανεμημένες τυχαίες μεταβλητές,
X(1)=min( X 1 , X 2 ,…, X n), X(n)=max( X 1 , X 2 ,…, X n).
Σε μια σειρά από εφαρμοσμένα προβλήματα μεγάλο ρόλοπαίζω Χ(1) Και Χ(n) , ειδικότερα, κατά τη μελέτη των μέγιστων δυνατών τιμών ("αρχεία") ορισμένων αξιών, για παράδειγμα, ασφαλιστικές πληρωμές ή ζημίες λόγω εμπορικών κινδύνων, κατά τη μελέτη των ορίων ελαστικότητας και αντοχής του χάλυβα, ορισμένα χαρακτηριστικά αξιοπιστίας, και τα λοιπά. Φαίνεται ότι για μεγάλα n οι κατανομές Χ(1) Και Χ(n) , κατά κανόνα, περιγράφονται καλά από τις διανομές Weibull - Gnedenko. Θεμελιώδεις συνεισφορές στη μελέτη των διανομών Χ(1) Και Χ(n) εισήχθη από τον Σοβιετικό μαθηματικό B.V. Gnedenko. Τα έργα των V. Weibull, E. Gumbel, V.B. Νεβζόροβα, Ε.Μ. Kudlaev και πολλοί άλλοι ειδικοί.
Ας περάσουμε στην οικογένεια των διανομών γάμμα. Χρησιμοποιούνται ευρέως στην οικονομία και τη διαχείριση, τη θεωρία και την πράξη της αξιοπιστίας και των δοκιμών, σε διάφορους τομείς της τεχνολογίας, της μετεωρολογίας κ.λπ. Ειδικότερα, σε πολλές περιπτώσεις, η κατανομή γάμμα υπόκειται σε ποσότητες όπως η συνολική διάρκεια ζωής του προϊόντος, το μήκος της αλυσίδας των αγώγιμων σωματιδίων σκόνης, ο χρόνος που χρειάζεται το προϊόν για να φτάσει στην οριακή κατάσταση κατά τη διάβρωση, τη λειτουργία χρόνο μέχρι κη άρνηση, κ= 1, 2, …, κ.λπ. Το προσδόκιμο ζωής των ασθενών με χρόνιες παθήσεις, ο χρόνος για να επιτευχθεί ένα συγκεκριμένο αποτέλεσμα στη θεραπεία σε ορισμένες περιπτώσεις έχουν μια κατανομή γάμμα. Αυτή η κατανομή είναι η πλέον κατάλληλη για την περιγραφή της ζήτησης σε οικονομικά και μαθηματικά μοντέλα διαχείρισης αποθεμάτων (logistics).
Η πυκνότητα της κατανομής γάμμα έχει τη μορφή
 (17)
(17)
Η πυκνότητα πιθανότητας στον τύπο (17) προσδιορίζεται από τρεις παραμέτρους ένα, σι, ντο, Οπου ένα>0, σι>0. Εν έναείναι μια παράμετρος φόρμας, σι- παράμετρος κλίμακας και Με- παράμετρος μετατόπισης. Παράγοντας 1/Γ(α)είναι μια κανονικοποίηση, εισάγεται για να
![]()
Εδώ Γ(α)- μια από τις ειδικές συναρτήσεις που χρησιμοποιούνται στα μαθηματικά, η λεγόμενη "συνάρτηση γάμμα", με την οποία ονομάζεται επίσης η κατανομή που δίνεται από τον τύπο (17),

Σε ένα σταθερό ΕΝΑΟ τύπος (17) ορίζει μια οικογένεια κατανομών μετατόπισης κλίμακας που δημιουργείται από μια κατανομή με πυκνότητα
 (18)
(18)
Η κατανομή της μορφής (18) ονομάζεται τυπική κατανομή γάμμα. Λαμβάνεται από τον τύπο (17) με σι= 1 και Με= 0.
Μια ειδική περίπτωση κατανομών γάμμα στο ΕΝΑ= 1 είναι εκθετικές κατανομές (με λ = 1/σι). Με φυσικό ΕΝΑΚαι Με=0 οι κατανομές γάμμα ονομάζονται κατανομές Erlang. Από τα έργα του Δανού επιστήμονα K.A. Erlang (1878-1929), υπαλλήλου της τηλεφωνικής εταιρείας της Κοπεγχάγης, που σπούδασε το 1908-1922. η λειτουργία των τηλεφωνικών δικτύων ξεκίνησε η ανάπτυξη της θεωρίας της ουράς. Αυτή η θεωρία ασχολείται με την πιθανο-στατιστική μοντελοποίηση συστημάτων στα οποία η ροή των αιτημάτων εξυπηρετείται προκειμένου να ληφθούν οι βέλτιστες αποφάσεις. Οι κατανομές Erlang χρησιμοποιούνται στις ίδιες περιοχές εφαρμογής με τις εκθετικές κατανομές. Αυτό βασίζεται στο ακόλουθο μαθηματικό γεγονός: το άθροισμα των k ανεξάρτητων τυχαίων μεταβλητών που κατανέμονται εκθετικά με τις ίδιες παραμέτρους λ και Με, έχει κατανομή γάμμα με παράμετρο σχήματος α =κ, παράμετρος κλίμακας σι= 1/λ και η παράμετρος shift kc. Στο Με= 0 παίρνουμε την κατανομή Erlang.
Αν η τυχαία μεταβλητή Χέχει κατανομή γάμμα με παράμετρο σχήματος ΕΝΑτέτοια που ρε = 2 ένα- ένας ακέραιος αριθμός, σι= 1 και Με= 0, μετά 2 Χέχει κατανομή χ-τετράγωνο με ρεβαθμοί ελευθερίας.
Μια τυχαία μεταβλητή X με κατανομή gvmma έχει τα ακόλουθα χαρακτηριστικά:
Αναμενόμενη αξία Μ(Χ) =αβ + ντο,
διασπορά ρε(Χ) = σ 2 = αβ 2 ,
Ο συντελεστής διακύμανσης
ασυμμετρία ![]()
Υπέρβαση ![]()
Η κανονική κατανομή είναι μια ακραία περίπτωση της κατανομής γάμμα. Πιο συγκεκριμένα, έστω ότι το Z είναι μια τυχαία μεταβλητή με τυπική κατανομή γάμμα, δίνεται με τύπο(18). Επειτα
![]()
Για οποιονδηποτε πραγματικός αριθμός Χ, Οπου F(x)- τυπική συνάρτηση κανονικής κατανομής Ν(0,1).
Στην εφαρμοσμένη έρευνα χρησιμοποιούνται και άλλες παραμετρικές οικογένειες κατανομών, από τις οποίες το σύστημα καμπύλης Pearson, οι σειρές Edgeworth και Charlier είναι οι πιο γνωστές. Δεν λαμβάνονται υπόψη εδώ.
Διακεκριμένος κατανομές που χρησιμοποιούνται σε πιθανοτικές-στατιστικές μεθόδους λήψης αποφάσεων.Τις περισσότερες φορές, χρησιμοποιούνται τρεις οικογένειες διακριτών κατανομών - διωνυμική, υπεργεωμετρική και Poisson, καθώς και ορισμένες άλλες οικογένειες - γεωμετρικές, αρνητικές διωνυμικές, πολυωνυμικές, αρνητικές υπεργεωμετρικές κ.λπ.
Όπως ήδη αναφέρθηκε, η διωνυμική κατανομή γίνεται σε ανεξάρτητες δοκιμές, σε καθεμία από τις οποίες με μια πιθανότητα Rεμφανίζεται το συμβάν ΕΝΑ. Εάν ο συνολικός αριθμός δοκιμών nδεδομένου, τότε ο αριθμός των δοκιμών Υ, στο οποίο εμφανίστηκε το συμβάν ΕΝΑ, έχει διωνυμική κατανομή. Για μια διωνυμική κατανομή, η πιθανότητα να γίνει αποδεκτή ως τυχαία μεταβλητή Υαξίες yκαθορίζεται από τον τύπο
![]()
Αριθμός συνδυασμών από nστοιχεία από yγνωστό από τη συνδυαστική. Για όλα y, εκτός από 0, 1, 2, …, n, έχουμε Π(Υ= y)= 0. Διωνυμική κατανομή με σταθερό μέγεθος δείγματος nορίζεται από την παράμετρο Π, δηλ. Οι διωνυμικές κατανομές σχηματίζουν μια οικογένεια μιας παραμέτρου. Χρησιμοποιούνται στην ανάλυση δεδομένων δείγματα μελετών, ειδικότερα, κατά τη μελέτη των προτιμήσεων των καταναλωτών, επιλεκτικός έλεγχος ποιότητας προϊόντων σύμφωνα με σχέδια ελέγχου ενός σταδίου, κατά τη δοκιμή πληθυσμών ατόμων στη δημογραφία, την κοινωνιολογία, την ιατρική, τη βιολογία κ.λπ.
Αν Υ 1 Και Υ 2 - ανεξάρτητες διωνυμικές τυχαίες μεταβλητές με την ίδια παράμετρο Π 0 προσδιορίζεται από δείγματα με όγκους n 1 Και n 2 αντίστοιχα, λοιπόν Υ 1 + Υ 2 - διωνυμική τυχαία μεταβλητή με κατανομή (19) με R = Π 0 Και n= n 1 + n 2 . Αυτή η παρατήρηση επεκτείνει τη δυνατότητα εφαρμογής της διωνυμικής κατανομής, επιτρέποντάς σας να συνδυάσετε τα αποτελέσματα πολλών ομάδων δοκιμών, όταν υπάρχει λόγος να πιστεύετε ότι η ίδια παράμετρος αντιστοιχεί σε όλες αυτές τις ομάδες.
Τα χαρακτηριστικά της διωνυμικής κατανομής υπολογίστηκαν νωρίτερα:
Μ(Υ) = np, ρε(Υ) = np( 1- Π).
Στην ενότητα "Γεγονότα και πιθανότητες" για μια διωνυμική τυχαία μεταβλητή, αποδεικνύεται ο νόμος των μεγάλων αριθμών:
![]()
Για οποιονδηποτε . Με τη βοήθεια του κεντρικού οριακού θεωρήματος, ο νόμος των μεγάλων αριθμών μπορεί να τελειοποιηθεί υποδεικνύοντας πώς Υ/ nδιαφέρει από R.
Θεώρημα De Moivre-Laplace.Για οποιουσδήποτε αριθμούς α και σι, ένα< σι, έχουμε

Οπου φά(Χ) είναι μια τυπική συνάρτηση κανονικής κατανομής με μέσο όρο 0 και διακύμανση 1.
Για να το αποδείξουμε, αρκεί να χρησιμοποιήσουμε την παράσταση Υως άθροισμα ανεξάρτητων τυχαίων μεταβλητών που αντιστοιχούν στα αποτελέσματα μεμονωμένων δοκιμών, τύποι για Μ(Υ) Και ρε(Υ) και το κεντρικό οριακό θεώρημα.
Αυτό το θεώρημα είναι για την περίπτωση R= S αποδείχθηκε από τον Άγγλο μαθηματικό A. Moivre (1667-1754) το 1730. Στην παραπάνω διατύπωση, το απέδειξε το 1810 ο Γάλλος μαθηματικός Pierre Simon Laplace (1749-1827).
Η υπεργεωμετρική κατανομή λαμβάνει χώρα κατά τον επιλεκτικό έλεγχο ενός πεπερασμένου συνόλου αντικειμένων όγκου Ν σύμφωνα με ένα εναλλακτικό χαρακτηριστικό. Κάθε ελεγχόμενο αντικείμενο ταξινομείται είτε ότι έχει το χαρακτηριστικό ΕΝΑ, ή ότι δεν διαθέτει αυτό το χαρακτηριστικό. Η υπεργεωμετρική κατανομή έχει μια τυχαία μεταβλητή Υ, ίσο με τον αριθμό των αντικειμένων που έχουν το χαρακτηριστικό ΕΝΑσε ένα τυχαίο δείγμα όγκου n, Οπου n< Ν. Για παράδειγμα, αριθμός Υελαττωματικές μονάδες προϊόντων σε ένα τυχαίο δείγμα όγκου nαπό τον όγκο παρτίδας Νέχει υπεργεωμετρική κατανομή αν n< Ν. Ένα άλλο παράδειγμα είναι η λοταρία. Αφήστε το σημάδι ΕΝΑένα δελτίο είναι ένα σημάδι «να κερδίζεις». Αφήστε όλα τα εισιτήρια Ν, και κάποιο άτομο έχει αποκτήσει nαπό αυτούς. Τότε ο αριθμός των κερδισμένων δελτίων για αυτό το άτομο έχει υπεργεωμετρική κατανομή.
Για μια υπεργεωμετρική κατανομή, η πιθανότητα μια τυχαία μεταβλητή Y να πάρει την τιμή y έχει τη μορφή
 (20)
(20)
Οπου ρεείναι ο αριθμός των αντικειμένων που έχουν το χαρακτηριστικό ΕΝΑ, στο εξεταζόμενο σύνολο όγκου Ν. Εν yπαίρνει τιμές από το max(0, n - (Ν - ρε)) έως ελάχιστα ( n, ρε), με άλλα yη πιθανότητα στον τύπο (20) είναι ίση με 0. Έτσι, η υπεργεωμετρική κατανομή καθορίζεται από τρεις παραμέτρους - τον όγκο πληθυσμός Ν, αριθμός αντικειμένων ρεσε αυτό, κατέχοντας το θεωρούμενο χαρακτηριστικό ΕΝΑκαι μέγεθος δείγματος n.
Απλή τυχαία δειγματοληψία nαπό τον συνολικό όγκο Νονομάζεται δείγμα που λαμβάνεται ως αποτέλεσμα τυχαίας επιλογής, στο οποίο οποιοδήποτε από τα σύνολα από nτα αντικείμενα έχουν την ίδια πιθανότητα να επιλεγούν. Μέθοδοι τυχαίας επιλογής δειγμάτων ερωτηθέντων (συνεντευξιαζόμενων) ή μονάδων προϊόντων τεμαχίου εξετάζονται στα διδακτικά-μεθοδικά και κανονιστικά-τεχνικά έγγραφα. Μία από τις μεθόδους επιλογής είναι η εξής: τα αντικείμενα επιλέγονται το ένα από το άλλο και σε κάθε βήμα καθένα από τα υπόλοιπα αντικείμενα στο σύνολο έχει την ίδια πιθανότητα να επιλεγεί. Στη βιβλιογραφία, για τον τύπο των δειγμάτων που εξετάζουμε, χρησιμοποιούνται και οι όροι «τυχαίο δείγμα», «τυχαίο δείγμα χωρίς αντικατάσταση».
Δεδομένου ότι οι όγκοι του γενικού πληθυσμού (παρτίδες) Νκαι δείγματα nείναι κοινώς γνωστά, τότε η παράμετρος υπεργεωμετρικής κατανομής που πρέπει να εκτιμηθεί είναι ρε. Σε στατιστικές μεθόδους διαχείρισης ποιότητας προϊόντων ρε- συνήθως ο αριθμός των ελαττωματικών μονάδων στην παρτίδα. Ενδιαφέρον παρουσιάζει και το χαρακτηριστικό της διανομής ρε/ Ν- επίπεδο ελαττώματος.
Για υπεργεωμετρική κατανομή
Ο τελευταίος παράγοντας στην έκφραση διακύμανσης είναι κοντά στο 1 if Ν>10 n. Αν, ταυτόχρονα, κάνουμε την αντικατάσταση Π = ρε/ Ν, τότε οι εκφράσεις για τη μαθηματική προσδοκία και διακύμανση της υπεργεωμετρικής κατανομής θα μετατραπούν σε εκφράσεις για τη μαθηματική προσδοκία και διακύμανση της διωνυμικής κατανομής. Αυτό δεν είναι τυχαίο. Μπορεί να αποδειχθεί ότι

στο Ν>10 n, Οπου Π = ρε/ Ν. Ο περιοριστικός λόγος ισχύει
και αυτή η περιοριστική σχέση μπορεί να χρησιμοποιηθεί για Ν>10 n.
Η τρίτη ευρέως χρησιμοποιούμενη διακριτή διανομή είναι η διανομή Poisson. Μια τυχαία μεταβλητή Υ έχει κατανομή Poisson αν
 ,
,
όπου λ είναι η παράμετρος κατανομής Poisson, και Π(Υ= y)= 0 για όλους τους άλλους y(για y=0, συμβολίζεται 0!=1). Για τη διανομή Poisson
Μ(Υ) = λ, ρε(Υ) = λ.
Αυτή η κατανομή πήρε το όνομά του από τον Γάλλο μαθηματικό C.D. Poisson (1781-1840), ο οποίος την παρήγαγε για πρώτη φορά το 1837. Η κατανομή Poisson είναι μια ακραία περίπτωση της διωνυμικής κατανομής, όπου η πιθανότητα Rη υλοποίηση της εκδήλωσης είναι μικρή, αλλά ο αριθμός των δοκιμών nυπέροχο, και np= λ. Πιο συγκεκριμένα, η σχέση ορίου
Επομένως, η διανομή Poisson (στην παλιά ορολογία «νόμος διανομής») αποκαλείται συχνά και «νόμος των σπάνιων γεγονότων».
Η κατανομή Poisson προκύπτει στη θεωρία των ροών γεγονότων (βλ. παραπάνω). Αποδεικνύεται ότι για την απλούστερη ροή με σταθερή ένταση Λ, ο αριθμός των γεγονότων (κλήσεων) που συνέβησαν κατά τη διάρκεια του χρόνου t, έχει κατανομή Poisson με παράμετρο λ = Λ t. Επομένως, η πιθανότητα ότι εν καιρώ tκανένα συμβάν δεν θα συμβεί μι - Λ t, δηλ. η συνάρτηση κατανομής του μήκους του διαστήματος μεταξύ των γεγονότων είναι εκθετική.
Η κατανομή Poisson χρησιμοποιείται στην ανάλυση των αποτελεσμάτων των επιλεκτικών ερευνών μάρκετινγκ των καταναλωτών, στον υπολογισμό των λειτουργικών χαρακτηριστικών των στατιστικών σχεδίων ελέγχου αποδοχής σε περίπτωση μικρών τιμών του επιπέδου αποδοχής ελαττωματικών, για να περιγράψει τον αριθμό των βλαβών μιας στατιστικά ελεγχόμενης τεχνολογική διαδικασίαανά μονάδα χρόνου, ο αριθμός των «απαιτήσεων για εξυπηρέτηση» που εισέρχονται στο σύστημα αναμονής ανά μονάδα χρόνου, στατιστικά πρότυπα ατυχημάτων και σπάνιων ασθενειών κ.λπ.
Περιγραφή άλλων παραμετρικών οικογενειών διακριτών κατανομών και οι δυνατότητές τους πρακτική χρήσηθεωρούνται στη βιβλιογραφία.
Σε ορισμένες περιπτώσεις, για παράδειγμα, κατά τη μελέτη τιμών, όγκων παραγωγής ή συνολικού χρόνου μεταξύ αστοχιών σε προβλήματα αξιοπιστίας, οι συναρτήσεις κατανομής είναι σταθερές σε ορισμένα διαστήματα στα οποία οι τιμές των τυχαίων μεταβλητών υπό μελέτη δεν μπορούν να πέσουν.
| Προηγούμενος |
………………………………………………………
An - μια τυχαία μεταβλητή X έχει πάρει την τιμή An.
Προφανώς, το άθροισμα των γεγονότων A1 A2, . , Το An είναι ένα ορισμένο γεγονός, αφού η τυχαία μεταβλητή παίρνει απαραίτητα τουλάχιστον μία από τις τιμές x1, x2, xn.
Επομένως, P (A1 È A2 È . È An) = 1.
Επιπλέον, τα συμβάντα A1, A2, ., An είναι ασύμβατα, καθώς μια τυχαία μεταβλητή σε ένα μόνο πείραμα μπορεί να λάβει μόνο μία από τις τιμές x1, x2, ., xn. Με το θεώρημα πρόσθεσης για ασύμβατα γεγονότα, λαμβάνουμε
P(A1)+P(A2)+ .+P(An)=1,
δηλ. p1+p2+. +pn = 1 ή, εν συντομία,
Επομένως, το άθροισμα όλων των αριθμών που βρίσκονται στη δεύτερη σειρά του Πίνακα 1, που δίνει τον νόμο κατανομής της τυχαίας μεταβλητής X, πρέπει να είναι ίσο με ένα.
ΠΑΡΑΔΕΙΓΜΑ 1. Έστω ότι η τυχαία μεταβλητή X είναι ο αριθμός των σημείων που κυλίονται όταν τυλίγεται μια μήτρα. Βρείτε τον νόμο κατανομής (με τη μορφή πίνακα).
Η τυχαία μεταβλητή Χ παίρνει τιμές
x1=1, x2=2, … , x6=6
με πιθανότητες
p1= p2 = … = p6 =
Ο νόμος διανομής δίνεται από τον πίνακα:
πίνακας 2
ΠΑΡΑΔΕΙΓΜΑ 2.Διωνυμική κατανομή. Θεωρήστε μια τυχαία μεταβλητή X - ο αριθμός των εμφανίσεων του γεγονότος Α σε μια σειρά από ανεξάρτητα πειράματα, σε καθένα από τα οποία το Α εμφανίζεται με πιθανότητα p.
Η τυχαία μεταβλητή X μπορεί προφανώς να λάβει μία από τις ακόλουθες τιμές:
0, 1, 2, ., k, ., n.
Η πιθανότητα ενός γεγονότος που συνίσταται στο γεγονός ότι η τυχαία μεταβλητή X θα λάβει τιμή ίση με k προσδιορίζεται από τον τύπο Bernoulli:
Рn(k)= όπου q=1- р.
Μια τέτοια κατανομή μιας τυχαίας μεταβλητής ονομάζεται διωνυμική κατανομή ή κατανομή Bernoulli. Η κατανομή Bernoulli καθορίζεται πλήρως από δύο παραμέτρους: τον αριθμό n όλων των δοκιμών και την πιθανότητα p με την οποία συμβαίνει το συμβάν σε κάθε μεμονωμένη δοκιμή.
Η συνθήκη για τη διωνυμική κατανομή έχει τη μορφή:
![]()
Για να αποδειχθεί η εγκυρότητα αυτής της ισότητας, αρκεί η ταυτότητα
(q+px)n= ![]()
βάλε x=1.
ΠΑΡΑΔΕΙΓΜΑ 3.Κατανομή Poisson. Αυτό είναι το όνομα της κατανομής πιθανότητας της φόρμας:
Ρ(κ)= ![]() .
.
Καθορίζεται από μία μόνο (θετική) παράμετρο α. Εάν το ξ είναι μια τυχαία μεταβλητή που έχει κατανομή Poisson, τότε η αντίστοιχη παράμετρος a - είναι η μέση τιμή αυτής της τυχαίας μεταβλητής:
a=Mξ=, όπου M είναι η μαθηματική προσδοκία.
Η τυχαία μεταβλητή είναι:
ΠΑΡΑΔΕΙΓΜΑ 4.εκθετική κατανομή.
Αν ο χρόνος είναι τυχαία μεταβλητή, ας τη συμβολίσουμε με τ, έτσι ώστε
όπου 0<λ=const, t ³ 0, причем, если t=0, то P(t)=0.
Η μέση τιμή της τυχαίας μεταβλητής t είναι:

Η πυκνότητα κατανομής έχει τη μορφή:

4) Κανονική κατανομή
Έστω ανεξάρτητες, πανομοιότυπα κατανεμημένες τυχαίες μεταβλητές και ας ![]() Εάν οι όροι είναι αρκετά μικροί και ο αριθμός n είναι αρκετά μεγάλος, - εάν για n à ∞ η μαθηματική προσδοκία της τυχαίας μεταβλητής Μξ και η διακύμανση Dξ ίση με Dξ=M(ξ–Μξ)2, είναι τέτοια ώστε Μξ~ α, Dξ~σ2, τότε
Εάν οι όροι είναι αρκετά μικροί και ο αριθμός n είναι αρκετά μεγάλος, - εάν για n à ∞ η μαθηματική προσδοκία της τυχαίας μεταβλητής Μξ και η διακύμανση Dξ ίση με Dξ=M(ξ–Μξ)2, είναι τέτοια ώστε Μξ~ α, Dξ~σ2, τότε
 - κανονική ή γκαουσιανή κατανομή
- κανονική ή γκαουσιανή κατανομή
![]() .
.
5) Γεωμετρική κατανομή. Έστω ξ που σημαίνει τον αριθμό των δοκιμών που προηγούνται της πρώτης «επιτυχίας». Αν υποθέσουμε ότι κάθε δοκιμή διαρκεί μια μονάδα χρόνου, τότε μπορούμε να θεωρήσουμε το ξ ως τον χρόνο αναμονής μέχρι την πρώτη «επιτυχία». Η διανομή μοιάζει με:
Р(k)=p(1-p)k, (k=0, 1, 2) p>0
6) Υπεργεωμετρική κατανομή.
Υπάρχουν N - αντικείμενα μεταξύ των οποίων n - "ειδικά αντικείμενα". Μεταξύ όλων των αντικειμένων, τα k-αντικείμενα επιλέγονται τυχαία. Βρείτε την πιθανότητα μεταξύ των επιλεγμένων αντικειμένων να ισούται με r - "ειδικά αντικείμενα". Η διανομή μοιάζει με:
7) Κατανομή Pascal.
Έστω x ο συνολικός αριθμός των "αστοχιών" που προηγούνται της άφιξης της rης "επιτυχίας". Η διανομή μοιάζει με:
Η συνάρτηση διανομής έχει τη μορφή:

Μια ισοπιθανή κατανομή σημαίνει ότι η τυχαία μεταβλητή x μπορεί να πάρει οποιαδήποτε τιμή στο διάστημα με την ίδια πιθανότητα. Στην περίπτωση αυτή, η πυκνότητα κατανομής υπολογίζεται ως 
Παρακάτω παρουσιάζονται γραφικές παραστάσεις πυκνότητας κατανομής και συνάρτησης κατανομής.

Πριν εξηγήσουμε την έννοια του "λευκού θορύβου", είναι απαραίτητο να δώσουμε ορισμένους ορισμούς.
Μια τυχαία συνάρτηση είναι μια συνάρτηση ενός μη τυχαίου ορίσματος t, το οποίο, για κάθε σταθερή τιμή του ορίσματος, είναι μια τυχαία μεταβλητή. Για παράδειγμα, εάν το U είναι μια τυχαία μεταβλητή, τότε η συνάρτηση X(t)=t2U είναι τυχαία.
Το τμήμα μιας τυχαίας συνάρτησης είναι μια τυχαία μεταβλητή που αντιστοιχεί σε μια σταθερή τιμή του ορίσματος της τυχαίας συνάρτησης. Ετσι, τυχαία συνάρτησημπορεί να θεωρηθεί ως ένα σύνολο τυχαίων μεταβλητών (X(t)), ανάλογα με την παράμετρο t.
Ορισμός 13.1.Καλείται η τυχαία μεταβλητή Χ διακεκριμένος, εάν χρειάζεται ένας πεπερασμένος ή μετρήσιμος αριθμός τιμών.
Ορισμός 13.2. Ο νόμος κατανομής μιας τυχαίας μεταβλητής Χείναι το σύνολο των ζευγών αριθμών ( , ), όπου βρίσκονται οι πιθανές τιμές της τυχαίας μεταβλητής και είναι οι πιθανότητες με τις οποίες η τυχαία μεταβλητή παίρνει αυτές τις τιμές, δηλ. =P( Χ= ), και =1.
Η απλούστερη μορφή καθορισμού μιας διακριτής τυχαίας μεταβλητής είναι ένας πίνακας που παραθέτει τις πιθανές τιμές μιας τυχαίας μεταβλητής και τις αντίστοιχες πιθανότητες. Ένας τέτοιος πίνακας ονομάζεται κοντά σε διανομήδιακριτή τυχαία μεταβλητή.
| Χ | … | … | |||
| R | … | … |
Η σειρά διανομής μπορεί να αναπαρασταθεί γραφικά. Στην περίπτωση αυτή, η τετμημένη σχεδιάζεται κατά μήκος της τεταγμένης και η πιθανότητα κατά μήκος της τεταγμένης. Τα σημεία με συντεταγμένες ( , ) συνδέονται με τμήματα και καλείται μια διακεκομμένη γραμμή πολύγωνο διανομής,που είναι μια από τις μορφές προσδιορισμού του νόμου κατανομής μιας διακριτής τυχαίας μεταβλητής.
Παράδειγμα 13.3.Κατασκευάστε ένα πολύγωνο κατανομής μιας τυχαίας μεταβλητής Χ με μια σειρά κατανομής
| Χ | ||||
| R | 0,1 | 0,3 | 0,2 | 0,4 |
Ορισμός 13.4.Λέμε ότι μια διακριτή τυχαία μεταβλητή Χ έχει διωνυμική κατανομήμε παραμέτρους ( n,p) εάν μπορεί να λάβει μη αρνητικές ακέραιες τιμές κ {1,2,…,n) με πιθανότητες Р( X=x)= .
Η σειρά διανομής έχει τη μορφή:
| Χ | … | κ | … | n | ||
| R | … | … |
Άθροισμα πιθανοτήτων = =1.
Ορισμός 13.5.Λέγεται ότι η διακριτή μορφή της τυχαίας μεταβλητής ΧΕχει Κατανομή Poissonμε την παράμετρο (>0), αν παίρνει ακέραιες τιμές κ(0,1,2,…) με πιθανότητες Р( X=k)= .
Η σειρά διανομής έχει τη μορφή
| Χ | … | κ | … | ||
| R | … | … |
Εφόσον η επέκταση στη σειρά Maclaurin έχει την ακόλουθη μορφή, τότε το άθροισμα των πιθανοτήτων = = =1.
Σημειώστε με Χαριθμός δοκιμών που πρέπει να ολοκληρωθούν πριν από την πρώτη εμφάνιση του συμβάντος ΕΝΑσε ανεξάρτητες δοκιμές, αν η πιθανότητα εμφάνισης του Α σε καθεμία από αυτές είναι ίση με Π (0<Π <1), а вероятность непоявления . Возможными значениями Χείναι φυσικοί αριθμοί.
Ορισμός 13.6.Λένε ότι η τυχαία μεταβλητή ΧΕχει γεωμετρική κατανομήμε παράμετρο Π (0<Π <1), если она принимает натуральные значения κ N με πιθανότητες Р(Х=k)= , όπου . Εύρος διανομής:
| Χ | … | n | … | |||
| R | … | … |
Το άθροισμα των πιθανοτήτων = = =1.
Παράδειγμα 13.7.Το κέρμα αναποδογυρίζεται 2 φορές. Συντάξτε μια σειρά κατανομής μιας τυχαίας μεταβλητής Χ του αριθμού των εμφανίσεων του «οικόσημου».
P 2 (0)= = ; P 2 (1)===0,5; P 2 (2) = = .
| Χ | |||
| R |
Η σειρά διανομής θα έχει τη μορφή:
Παράδειγμα 13.8.Το όπλο εκτοξεύεται μέχρι το πρώτο χτύπημα στο στόχο. Η πιθανότητα να χτυπήσετε με μία βολή είναι 0,6. θα χτυπήσει στην 3η βολή.
Επειδή η Π=0,6, q=0,4, κ=3, μετά P( ΕΝΑ)= =0,4 2 *0,6=0,096.
14 Αριθμητικά χαρακτηριστικά διακριτών τυχαίων μεταβλητών
Ο νόμος κατανομής χαρακτηρίζει πλήρως την τυχαία μεταβλητή, αλλά συχνά είναι άγνωστη, επομένως πρέπει να περιοριστείτε σε λιγότερες πληροφορίες. Μερικές φορές είναι ακόμη πιο κερδοφόρο να χρησιμοποιείτε αριθμούς (παραμέτρους) που περιγράφουν την τυχαία μεταβλητή συνολικά. Καλούνται αριθμητικά χαρακτηριστικάτυχαία μεταβλητή. Αυτά περιλαμβάνουν: μαθηματική προσδοκία, διακύμανση κ.λπ.
Ορισμός 14.1. μαθηματική προσδοκίαΜια διακριτή τυχαία μεταβλητή ονομάζεται το άθροισμα των γινομένων όλων των πιθανών τιμών της και των πιθανοτήτων τους. Δηλώστε τη μαθηματική προσδοκία μιας τυχαίας μεταβλητής Χμέσω του Μ Χ=M( Χ)=Ε Χ.
Αν η τυχαία μεταβλητή Χπαίρνει έναν πεπερασμένο αριθμό τιμών, μετά το M Χ= .
Αν η τυχαία μεταβλητή Χπαίρνει έναν μετρήσιμο αριθμό τιμών και μετά το M Χ= ,
και η μαθηματική προσδοκία υπάρχει αν η σειρά συγκλίνει απόλυτα.
Παρατήρηση 14.2.Η μαθηματική προσδοκία είναι ένας ορισμένος αριθμός περίπου ίσος με μια ορισμένη τιμή μιας τυχαίας μεταβλητής.
Παράδειγμα 14.3.Βρείτε τη μαθηματική προσδοκία μιας τυχαίας μεταβλητής Χ, γνωρίζοντας τη σειρά διανομής του
| Χ | |||
| R | 0,1 | 0,6 | 0,3 |
Μ Χ=3*0,1+5*0,6+2*0,3=3,9.
Παράδειγμα 14.4.Να βρείτε τη μαθηματική προσδοκία του αριθμού των εμφανίσεων ενός γεγονότος ΕΝΑσε μία δοκιμή, εάν η πιθανότητα ενός γεγονότος ΕΝΑείναι ίσο με Π.
Τυχαία τιμή Χ- αριθμός εμφάνισης του συμβάντος ΕΝΑσε ένα τεστ. Μπορεί να πάρει τιμές =1 ( ΕΝΑσυνέβη) με πιθανότητα Πκαι =0 με πιθανότητα , δηλ. σειρά διανομής
Επομένως MS=C*1=C.
Παρατήρηση 14.6.Το γινόμενο μιας σταθερής τιμής C από μια διακριτή τυχαία μεταβλητή ΧΟρίζεται ως μια διακριτή τυχαία μεταβλητή C Χ, οι πιθανές τιμές των οποίων είναι ίσες με τα γινόμενα της σταθεράς С και τις πιθανές τιμές Χ, οι πιθανότητες αυτών των τιμών · С Χείναι ίσες με τις πιθανότητες των αντίστοιχων δυνατών τιμών Χ.
Ιδιοκτησία 14.7.Ο σταθερός παράγοντας μπορεί να αφαιρεθεί από το σημάδι της προσδοκίας:
ΚΥΡΙΑ Χ)=C∙M Χ.
Αν η τυχαία μεταβλητή Χέχει αριθμό διανομής
| Χ | … | … | |||
| R | … | … |
Σειρά διανομής τυχαίας μεταβλητής
| SH | … | … | |||
| R | … | … |
ΚΥΡΙΑ Χ)= = = С∙М( Χ).
Ορισμός 14.8.Οι τυχαίες μεταβλητές , ,…, καλούνται ανεξάρτητος, εάν για , Εγώ=1,2,…,n
Р( , ,…, )= Р( ) Р( )… Р( ) (1)
Αν ως = , Εγώ=1,2,…,n, τότε λαμβάνουμε από το (1)
R(< , < ,…, < }= Р{ < }Р{ < }… Р{ < }, откуда получается другая формула:
( , ,…, ) = () ()... () (2)
για τη συνάρτηση κοινής κατανομής τυχαίων μεταβλητών , ,…, , η οποία μπορεί επίσης να ληφθεί ως ορισμός της ανεξαρτησίας μιας τυχαίας μεταβλητής.
Ιδιοκτησία 14.9.Μαθηματική προσδοκία του γινομένου του 2 ανεξάρτητοςΟι τυχαίες μεταβλητές είναι ίσες με το γινόμενο των μαθηματικών προσδοκιών τους:
Μ( XY)=Μ Χ∙Μ Στο.
Ακίνητο 14.10.Η μαθηματική προσδοκία του αθροίσματος 2 τυχαίων μεταβλητών είναι ίση με το άθροισμα των μαθηματικών προσδοκιών τους:
Μ( Χ+Υ)=Μ Χ+Μ Στο.
Παρατήρηση 14.11.Οι ιδιότητες 14.9 και 14.10 μπορούν να γενικευθούν στην περίπτωση πολλών τυχαίων μεταβλητών.
Παράδειγμα 14.12.Βρείτε τη μαθηματική προσδοκία του αθροίσματος του αριθμού των πόντων που μπορεί να πέσει όταν ρίχνετε 2 ζάρια.
Αφήνω Χο αριθμός των πόντων που κυλήθηκαν στο πρώτο ζάρι, Στοο αριθμός των πόντων που κυλήθηκαν στο δεύτερο ζάρι. Έχουν την ίδια σειρά διανομής:
| Χ | ||||||
| R |
Στη συνέχεια ο Μ Χ=Μ Στο= (1+2+3+4+5+6)= = . Μ( Χ+Υ)=2* =7.
Θεώρημα 14.13.Μαθηματική προσδοκία του αριθμού των εμφανίσεων του γεγονότος ΕΝΑ V nανεξάρτητες δοκιμές ισούται με το γινόμενο του αριθμού των δοκιμών και της πιθανότητας να συμβεί ένα συμβάν σε κάθε δοκιμή: M Χ=np.
Αφήνω Χ– αριθμός περιστατικών του συμβάντος ΕΝΑ V nανεξάρτητα τεστ. – αριθμός περιστατικών του συμβάντος ΕΝΑ V Εγώ- αυτό το τεστ, Εγώ=1,2,…,n.Τότε = + +…+ . Σύμφωνα με τις ιδιότητες της μαθηματικής προσδοκίας Μ Χ= . Από το παράδειγμα 14,4M X i=πι=1,2,…,n,εξ ου και ο Μ Χ= =np.
Ορισμός 14.14.διασποράΗ τυχαία μεταβλητή ονομάζεται αριθμός D Χ=M( Χ-Μ Χ) 2 .
Ορισμός 14.15.Τυπική απόκλισητυχαία μεταβλητή Χκαλούμενος αριθμός =.
Παρατήρηση 14.16.Η διασπορά είναι ένα μέτρο της εξάπλωσης των τιμών μιας τυχαίας μεταβλητής γύρω από τις μαθηματικές προσδοκίες της. Είναι πάντα μη αρνητικό. Για να υπολογίσετε τη διακύμανση, είναι πιο βολικό να χρησιμοποιήσετε έναν άλλο τύπο:
ρε Χ=M( Χ-Μ Χ) 2 = M( Χ 2 - 2X∙Μ Χ+ (Μ Χ) 2) = M( Χ 2) - 2 εκατ.( X∙Μ Χ) + Μ(Μ Χ) 2 = =M( Χ 2)-Μ X∙Μ X+(Μ Χ) 2 = Μ( Χ 2) - (Μ Χ) 2 .
Από εδώ ο Δ Χ=M( Χ 2) - (Μ Χ) 2 .
Παράδειγμα 14.17.Βρείτε τη διακύμανση μιας τυχαίας μεταβλητής Χ, που δίνεται από έναν αριθμό διανομών
| Χ | |||
| Π | 0,1 | 0,6 | 0,3 |
Μ Χ=2*0,1+3*0,6+5*0,3=3,5; Μ( Χ 2)= 4*0,1+9*0,6+25*0,3=13,3;
ρε Χ=13.3-(3,5) 2 =1,05.
Ιδιότητες διασποράς
Ιδιοκτησία 14.18.Η διασπορά μιας σταθερής τιμής είναι 0:
DC = M(C-MC) 2 = M(C-C) 2 =0.
Ιδιοκτησία 14.19.Ο σταθερός παράγοντας μπορεί να αφαιρεθεί από το πρόσημο διασποράς τετραγωνίζοντάς το
Δ(Γ Χ) = C 2 D Χ.
D(CX)=M(C-CM Χ) 2 \u003d M (C (X- M Χ) 2) = C 2 M( Χ-Μ Χ) 2 = C 2 D Χ.
Ακίνητο 14.20.Η διακύμανση του αθροίσματος του 2 ανεξάρτητοςτυχαίες μεταβλητές ισούται με το άθροισμα των διακυμάνσεων αυτών των μεταβλητών
ΡΕ( Χ+Υ)=Δ Χ+Δ Υ.
ΡΕ( Χ + Υ)=M(( Χ+Υ) 2) – (Μ( Χ+Υ)) 2 = M( x2+ 2XY+Y2) - (Μ Χ+ Μ Υ) 2 = =M( Χ) 2 +2M ΧΜ Υ+M( Υ 2)-(M( Χ) 2 +2M ΧΜ Υ+M( Υ) 2) = M( Χ 2)-(Μ Χ) 2 +M( Υ 2)-(Μ Υ) 2 = Δ Χ+Δ Υ.
Συμπέρασμα 14.21.Η διακύμανση του αθροίσματος πολλών ανεξάρτητοςΟι τυχαίες μεταβλητές είναι ίσες με το άθροισμα των διακυμάνσεών τους.
Θεώρημα 14.22.Διακύμανση του αριθμού των εμφανίσεων ενός συμβάντος ΕΝΑ V nανεξάρτητα τεστ, σε καθένα από τα οποία η πιθανότητα p) 2 =). Ως εκ τούτου D +2,