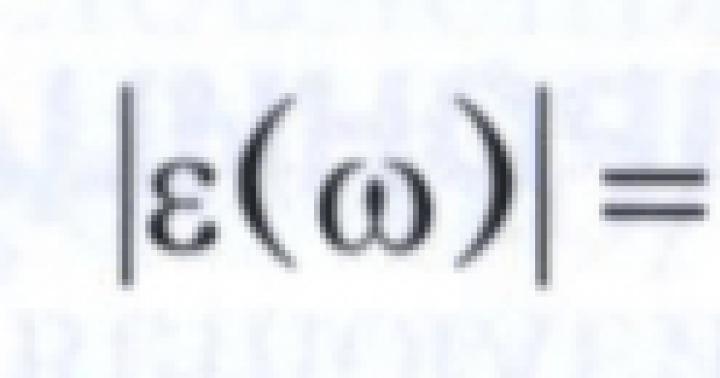Τι είναι μια συγκλίνουσα σειρά. Σημάδια σύγκλισης αριθμητικών σειρών. Σύγκλιση σειρών με θετικούς όρους

ΕΙΣΑΓΩΓΗ

Το εγχειρίδιο απευθύνεται σε καθηγητές μαθηματικών των τεχνικών σχολών, καθώς και σε δευτεροετείς μαθητές όλων των ειδικοτήτων.

Στην παρούσα εργασία παρουσιάζουμε τις βασικές έννοιες της θεωρίας των σειρών. Το θεωρητικό υλικό πληροί τις απαιτήσεις του Κρατικού Εκπαιδευτικού Προτύπου Δευτεροβάθμιας Επαγγελματικής Εκπαίδευσης (Υπουργείο Παιδείας Ρωσική Ομοσπονδία. Μ., 2002).

Η παρουσίαση του θεωρητικού υλικού για ολόκληρο το θέμα συνοδεύεται από εξέταση μεγάλου αριθμού παραδειγμάτων και εργασιών, που διεξάγονται σε προσβάσιμο, αν είναι δυνατόν αυστηρή γλώσσα. Στο τέλος του εγχειριδίου υπάρχουν παραδείγματα και εργασίες που μπορούν να εκτελέσουν οι μαθητές σε λειτουργία αυτοελέγχου.

Το εγχειρίδιο προορίζεται για φοιτητές αλληλογραφίας και μορφών εκπαίδευσης πλήρους απασχόλησης.

Λαμβάνοντας υπόψη το επίπεδο προετοιμασίας των μαθητών τεχνικών σχολών, καθώς και τον εξαιρετικά περιορισμένο αριθμό ωρών (12 ώρες + 4 λίβρες) που διαθέτει το πρόγραμμα για τη μετάβαση ανώτερων μαθηματικών στις τεχνικές σχολές, αυστηρά συμπεράσματα, τα οποία παρουσιάζουν μεγάλες δυσκολίες αφομοίωσης , παραλείπονται, περιορίζονται στην εξέταση παραδειγμάτων.

ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ

Η λύση ενός προβλήματος που παρουσιάζεται με μαθηματικούς όρους, για παράδειγμα, ως συνδυασμός διαφόρων συναρτήσεων, των παραγώγων και των ολοκληρωμάτων τους, πρέπει να είναι σε θέση να «φέρει σε έναν αριθμό», ο οποίος τις περισσότερες φορές χρησιμεύει ως η τελική απάντηση. Για αυτό, έχουν αναπτυχθεί διάφορες μέθοδοι σε διάφορους κλάδους των μαθηματικών.

Το τμήμα των μαθηματικών που επιτρέπει την επίλυση οποιουδήποτε καλά τεθέντος προβλήματος με επαρκή ακρίβεια για πρακτική χρήση ονομάζεται θεωρία των σειρών.

Έστω και κάποιες λεπτές έννοιες μαθηματική ανάλυσηεμφανίστηκαν εκτός της θεωρίας των σειρών, εφαρμόστηκαν αμέσως σε σειρές, οι οποίες χρησίμευσαν ως ένα είδος οργάνου για τον έλεγχο της σημασίας αυτών των εννοιών. Αυτή η κατάσταση συνεχίζεται μέχρι σήμερα.

Έκφραση της φόρμας

όπου ;;;…;;… είναι τα μέλη της σειράς; - απείρως μικρόςή κοινό μέλος μιας σειράς, ονομάζεται άπειρη σειρά (αριθμός).

Αν τα μέλη της σειράς:

I. Αριθμητική σειρά

1.1. Βασικές έννοιες της σειράς αριθμών.

Αριθμητική σειράονομάζεται άθροισμα της μορφής

, (1.1)

όπου τα ,,,…,,…, που ονομάζονται μέλη της σειράς, σχηματίζουν μια άπειρη ακολουθία. ένα μέλος ονομάζεται κοινό μέλος της σειράς.

που αποτελούνται από τους πρώτους όρους της σειράς (1.1) ονομάζονται επιμέρους αθροίσματα αυτής της σειράς.

Κάθε σειρά μπορεί να συσχετιστεί με μια ακολουθία μερικών αθροισμάτων .

Αν με άπειρη αύξηση του αριθμού nτο μερικό άθροισμα της σειράς τείνει προς το όριο, τότε η σειρά ονομάζεται συγκλίνουσα και ο αριθμός ονομάζεται άθροισμα της συγκλίνουσας σειράς, δηλ.

Αυτή η καταχώρηση είναι ισοδύναμη με την καταχώρηση

.

Αν το μερικό άθροισμα της σειράς (1.1) με απεριόριστη αύξηση nδεν έχει πεπερασμένο όριο ( τείνει προς ή ), τότε μια τέτοια σειρά ονομάζεται αποκλίνων .

Αν η σειρά συγκεντρούμενος , τότε η τιμή για αρκετά μεγάλο n είναι μια κατά προσέγγιση έκφραση για το άθροισμα της σειράς μικρό.

Η διαφορά ονομάζεται υπόλοιπο της σειράς. Εάν η σειρά συγκλίνει, τότε το υπόλοιπο της τείνει στο μηδέν, δηλ., και αντίστροφα, εάν το υπόλοιπο τείνει στο μηδέν, τότε η σειρά συγκλίνει.

1.2. Παραδείγματα σειρών αριθμών.

Παράδειγμα 1. Μια σειρά της φόρμας

(1.2)

που ονομάζεται γεωμετρικός .

Η γεωμετρική σειρά σχηματίζεται από τα μέλη μιας γεωμετρικής προόδου.

Είναι γνωστό ότι το άθροισμα του πρώτου του nμέλη. Προφανώς αυτό είναι n-το μερικό άθροισμα της σειράς (1.2).

Πιθανές περιπτώσεις:

Η σειρά (1.2) έχει τη μορφή:

, η σειρά αποκλίνει.

Η σειρά (1.2) έχει τη μορφή:

Δεν έχει όριο, η σειρά αποκλίνει.

είναι ένας πεπερασμένος αριθμός, η σειρά συγκλίνει.

- η σειρά αποκλίνει.

Ετσι, αυτή η σειράσυγκλίνει στο και αποκλίνει στο .

Παράδειγμα 2. Μια σειρά της φόρμας

(1.3)

που ονομάζεται αρμονικός .

Ας γράψουμε το μερικό άθροισμα αυτής της σειράς:

Το ποσό είναι μεγαλύτερο από το ποσό που παρουσιάζεται ως εξής:

ή .

Αν τότε , ή .

Επομένως, εάν , τότε , δηλ. η αρμονική σειρά αποκλίνει.

Παράδειγμα 3. Μια σειρά της φόρμας

(1.4)

που ονομάζεται γενικευμένη αρμονική .

Αν , τότε αυτή η σειρά μετατρέπεται σε αρμονική σειρά, η οποία είναι αποκλίνουσα.

Αν , τότε οι όροι αυτής της σειράς είναι μεγαλύτεροι από τους αντίστοιχους όρους της αρμονικής σειράς και, επομένως, αποκλίνει. Όταν έχουμε μια γεωμετρική σειρά στην οποία ? είναι συγκλίνουσα.

Έτσι, η γενικευμένη αρμονική σειρά συγκλίνει και αποκλίνει στο .

1.3. Απαραίτητα και επαρκή κριτήρια σύγκλισης.

Απαραίτητο κριτήριο για τη σύγκλιση μιας σειράς.

Η σειρά μπορεί να συγκλίνει μόνο εάν ο κοινός όρος της τείνει στο μηδέν καθώς ο αριθμός αυξάνεται χωρίς όριο: .

Εάν , τότε η σειρά αποκλίνει - αυτό είναι επαρκές κριτήριο για την απόκλιση της σειράς.

Επαρκείς προϋποθέσεις για τη σύγκλιση μιας σειράς με θετικούς όρους.

Σημάδι σύγκρισης σειρών με θετικούς όρους.

Η υπό μελέτη σειρά συγκλίνει εάν τα μέλη της δεν υπερβαίνουν τα αντίστοιχα μέλη μιας άλλης, προφανώς συγκλίνουσας σειράς. η υπό μελέτη σειρά αποκλίνει εάν οι όροι της υπερβαίνουν τους αντίστοιχους όρους μιας άλλης, προφανώς αποκλίνουσας σειράς.

Σημάδι του d'Alembert.

Αν για μια σειρά με θετικούς όρους

η συνθήκη ικανοποιείται, τότε η σειρά συγκλίνει στο και αποκλίνει στο .

Το σημάδι του d'Alembert δεν δίνει απάντηση αν . Σε αυτή την περίπτωση, χρησιμοποιούνται άλλες μέθοδοι για τη μελέτη της σειράς.

Γυμνάσια.

Γράψτε μια σειρά με τον δεδομένο κοινό όρο της:

Υποθέτοντας ,,,…, έχουμε μια άπειρη ακολουθία αριθμών:

Προσθέτοντας τους όρους της, παίρνουμε τη σειρά

.

Κάνοντας το ίδιο, παίρνουμε τη σειρά

.

Δίνοντας τις τιμές 1,2,3,… και λαμβάνοντας υπόψη ότι,,,…, παίρνουμε τη σειρά

.

Να βρω n-ο όρος της σειράς σύμφωνα με τους πρώτους όρους της:

Οι παρονομαστές των μελών της σειράς, ξεκινώντας από την πρώτη, είναι ζυγοί αριθμοί. ως εκ τούτου, n-Ο ος όρος της σειράς έχει τη μορφή .

Οι αριθμητές των μελών της σειράς σχηματίζουν μια φυσική σειρά αριθμών και οι αντίστοιχοι παρονομαστές μια φυσική σειρά αριθμών και οι αντίστοιχοι παρονομαστές μια φυσική σειρά αριθμών, ξεκινώντας από το 3. Τα σημεία εναλλάσσονται σύμφωνα με το νόμο ή σύμφωνα με στο νόμο. Που σημαίνει, n-Ο ος όρος της σειράς έχει τη μορφή . ή .

Διερευνήστε τη σύγκλιση της σειράς χρησιμοποιώντας το απαραίτητο τεστ σύγκλισης και το συγκριτικό τεστ:

;

.

Βρίσκουμε .

Το απαραίτητο κριτήριο για τη σύγκλιση της σειράς ικανοποιείται, αλλά για να λυθεί το ζήτημα της σύγκλισης πρέπει να εφαρμοστεί ένα από τα επαρκή κριτήρια σύγκλισης. Συγκρίνετε αυτή τη σειρά με τη γεωμετρική σειρά

,

που συγκλίνει από τότε.

Συγκρίνοντας τους όρους αυτής της σειράς, ξεκινώντας από τη δεύτερη, με τους αντίστοιχους όρους της γεωμετρικής σειράς, παίρνουμε τις ανισότητες

εκείνοι. οι όροι αυτής της σειράς, ξεκινώντας από τη δεύτερη, είναι αντίστοιχα μικρότεροι από τους όρους της γεωμετρικής σειράς, από την οποία προκύπτει ότι η δεδομένη σειρά συγκλίνει.

.

Εδώ, ικανοποιείται ένα επαρκές κριτήριο για την απόκλιση της σειράς. ως εκ τούτου η σειρά αποκλίνει.

Βρίσκουμε .

Το απαραίτητο κριτήριο για τη σύγκλιση της σειράς ικανοποιείται. Ας συγκρίνουμε αυτή τη σειρά με τη γενικευμένη αρμονική σειρά

,

που συγκλίνει, αφού, λοιπόν, συγκλίνει και η δεδομένη σειρά.

Διερευνήστε τη σύγκλιση της σειράς χρησιμοποιώντας το τεστ d'Alembert:

;

.

Αντικατάσταση στον κοινό όρο της σειράς αντί για nαριθμός n+ 1, παίρνουμε . Ας βρούμε το όριο του λόγου του -ου όρου προς n-μου μέλος στο:

Επομένως, αυτή η σειρά συγκλίνει.

Άρα αυτή η σειρά αποκλίνει.

Εκείνοι. η σειρά αποκλίνει.

II. εναλλασσόμενες σειρές

2.1 Η έννοια μιας εναλλασσόμενης σειράς.

Σειρά αριθμών

που ονομάζεται εναλλασσόμενος αν τα μέλη του περιλαμβάνουν και θετικούς και αρνητικούς αριθμούς.

Η αριθμητική γραμμή καλείται εναλλασσόμενος αν δύο παρακείμενοι όροι έχουν αντίθετα πρόσημα.

όπου για όλους (δηλαδή, μια σειρά της οποίας οι θετικοί και οι αρνητικοί όροι διαδέχονται ο ένας τον άλλον). Για παράδειγμα,

;

;

.

Για τις εναλλασσόμενες σειρές, υπάρχει ένα επαρκές κριτήριο για τη σύγκλιση (που καθιερώθηκε το 1714 από τον Leibniz σε μια επιστολή προς τον I. Bernoulli).

2.2 Σημάδι του Λάιμπνιτς. Απόλυτη και υπό όρους σύγκλιση της σειράς.

Θεώρημα (τεστ Leibniz).

Μια εναλλασσόμενη σειρά συγκλίνει εάν:

Η ακολουθία των απόλυτων τιμών των όρων της σειράς μειώνεται μονοτονικά, δηλ. ;

Ο κοινός όρος της σειράς τείνει στο μηδέν:.

Επιπλέον, το άθροισμα S της σειράς ικανοποιεί τις ανισότητες

Παρατηρήσεις.

Μελέτη εναλλασσόμενης σειράς της φόρμας

(με αρνητικό πρώτο όρο) μειώνεται πολλαπλασιάζοντας όλους τους όρους του επί στη μελέτη της σειράς .

Οι σειρές για τις οποίες ικανοποιούνται οι προϋποθέσεις του θεωρήματος του Leibniz ονομάζονται Leibnizian (ή σειρά Leibniz).

Η σχέση μας επιτρέπει να λάβουμε μια απλή και βολική εκτίμηση του σφάλματος που κάνουμε αντικαθιστώντας το άθροισμα μικρόαυτής της σειράς με το μερικό άθροισμά της.

Η απορριφθείσα σειρά (υπόλοιπο) είναι επίσης μια εναλλασσόμενη σειρά , το άθροισμα του οποίου είναι μικρότερο από τον πρώτο όρο αυτής της σειράς, δηλαδή, το σφάλμα είναι μικρότερο από το μέτρο του πρώτου από τους όρους που απορρίφθηκαν.

Παράδειγμα. Υπολογίστε περίπου το άθροισμα της σειράς.

Λύση: δεδομένη σειρά τύπου Leibniz. Συγκλίνει. Μπορείς να γράψεις:

.

Λαμβάνοντας πέντε θητείες, δηλ. αναπληρώσιμος

Ας κάνουμε ένα μικρότερο λάθος

πως . Ετσι,.

Για εναλλασσόμενες σειρές ισχύει το ακόλουθο γενικό επαρκές κριτήριο σύγκλισης.

Θεώρημα. Ας δοθεί μια εναλλασσόμενη σειρά

Αν η σειρά συγκλίνει

που αποτελείται από τους συντελεστές των μελών της δεδομένης σειράς, τότε η ίδια η εναλλασσόμενη σειρά συγκλίνει.

Το κριτήριο σύγκλισης Leibniz για εναλλασσόμενες σειρές είναι επαρκές κριτήριο για τη σύγκλιση εναλλασσόμενων σειρών.

Η εναλλασσόμενη σειρά ονομάζεται απολύτως συγκλίνουσα , εάν μια σειρά που αποτελείται από τις απόλυτες τιμές των μελών της συγκλίνει, δηλ. κάθε απολύτως συγκλίνουσα σειρά είναι συγκλίνουσα.

Εάν μια εναλλασσόμενη σειρά συγκλίνει και μια σειρά που αποτελείται από τις απόλυτες τιμές των μελών της αποκλίνει, τότε αυτή η σειρά ονομάζεται υπό όρους (όχι απόλυτο) συγκλίνουσα.

2.3. Γυμνάσια.

Εξετάστε για σύγκλιση (απόλυτη ή υπό όρους) μια εναλλασσόμενη σειρά:

και

Επομένως, σύμφωνα με το τεστ Leibniz, η σειρά συγκλίνει. Ας μάθουμε αν αυτή η σειρά συγκλίνει απολύτως ή υπό όρους.

Σειρά , που αποτελείται από τις απόλυτες τιμές της δεδομένης σειράς, είναι μια αρμονική σειρά που αποκλίνει. Επομένως, αυτή η σειρά συγκλίνει υπό όρους.

Οι όροι αυτής της σειράς μειώνονται μονοτονικά σε απόλυτη τιμή:

, αλλά

.

Η σειρά αποκλίνει επειδή το τεστ Leibniz δεν ισχύει.

Χρησιμοποιώντας το τεστ Leibniz, παίρνουμε

;,

εκείνοι. η σειρά συγκλίνει.

.

Αυτή είναι μια γεωμετρική σειρά της μορφής Where, η οποία συγκλίνει. Επομένως, αυτή η σειρά συγκλίνει απόλυτα.

Χρησιμοποιώντας το τεστ Leibniz, έχουμε

;

, δηλ. η σειρά συγκλίνει.

Εξετάστε μια σειρά που αποτελείται από τις απόλυτες τιμές των όρων αυτής της σειράς:

, ή

.

Αυτή είναι μια γενικευμένη αρμονική σειρά που αποκλίνει, αφού. Επομένως, αυτή η σειρά συγκλίνει υπό όρους.

III. Λειτουργικό εύρος

3.1. Η έννοια μιας λειτουργικής σειράς.

Μια σειρά της οποίας τα μέλη είναι συναρτήσεις ονομάζεται λειτουργικός :

Δίνοντας μια συγκεκριμένη τιμή, παίρνουμε μια σειρά αριθμών

που μπορεί να είναι είτε συγκλίνουσες είτε αποκλίνουσες.

Εάν η σειρά αριθμών που προκύπτει συγκλίνει, τότε το σημείο καλείται σημείο σύγκλισης λειτουργική σειρά? αν η σειρά αποκλίνει σημείο απόκλισης λειτουργική σειρά.

Το σύνολο των αριθμητικών τιμών του ορίσματος, στο οποίο συγκλίνει η συναρτησιακή σειρά, ονομάζεται περιοχή σύγκλισης .

Στην περιοχή σύγκλισης μιας συναρτησιακής σειράς, το άθροισμά της είναι μια ορισμένη συνάρτηση :.

Ορίζεται στην περιοχή σύγκλισης από την ισότητα

, που

Μερικό άθροισμα μιας σειράς.

Παράδειγμα. Βρείτε την περιοχή σύγκλισης της σειράς.

Απόφαση. Αυτή η σειρά είναι μια σειρά γεωμετρικής προόδου με παρονομαστή . Επομένως, αυτή η σειρά συγκλίνει για , δηλ. για όλα ; το άθροισμα της σειράς είναι ?

, στο .

3.2. Power σειρά.

Μια σειρά ισχύος είναι μια σειρά της μορφής

,

που είναι οι αριθμοί που ονομάζεται συντελεστές σειράς , και ο όρος είναι ένας κοινός όρος της σειράς.

Η περιοχή σύγκλισης μιας σειράς ισχύος είναι το σύνολο όλων των τιμών για τις οποίες συγκλίνει η σειρά.

Ο αριθμός καλείται ακτίνα σύγκλισης σειρά ισχύος, εάν για , η σειρά συγκλίνει και, επιπλέον, απολύτως, και για , η σειρά αποκλίνει.

Βρίσκουμε την ακτίνα σύγκλισης χρησιμοποιώντας τη δοκιμή d'Alembert:

(δεν εξαρτάται από),

εκείνοι. εάν η σειρά ισχύος συγκλίνει για οποιαδήποτε ικανοποιητική αυτή η συνθήκηκαι αποκλίνει στο .

Από αυτό προκύπτει ότι αν υπάρχει όριο

,

τότε η ακτίνα σύγκλισης της σειράς είναι ίση με αυτό το όριο και η σειρά ισχύος συγκλίνει στο , δηλ. μεταξύ των οποίων καλείται διάστημα (διάστημα) σύγκλισης.

Αν , τότε η σειρά ισχύος συγκλίνει σε ένα μόνο σημείο .

Στα άκρα του διαστήματος, η σειρά μπορεί να συγκλίνει (απόλυτα ή υπό όρους), αλλά μπορεί επίσης να αποκλίνει.

Η σύγκλιση της σειράς ισχύος για και διερευνάται χρησιμοποιώντας ένα από τα κριτήρια σύγκλισης.

3.3. Γυμνάσια.

Βρείτε την περιοχή σύγκλισης της σειράς:

Απόφαση. Βρείτε την ακτίνα σύγκλισης αυτής της σειράς:

.

Επομένως, αυτή η σειρά συγκλίνει απολύτως στον ακέραιο άξονα του αριθμού.

Απόφαση. Ας χρησιμοποιήσουμε το σύμβολο του d'Alembert. Για αυτή τη σειρά έχουμε:

.

Η σειρά συγκλίνει απολύτως εάν ή . Ας μελετήσουμε τη συμπεριφορά της σειράς στα άκρα του διαστήματος σύγκλισης.

Γιατί έχουμε μια σειρά

Γιατί έχουμε μια σειρά είναι επίσης μια συγκλίνουσα σειρά Leibniz. Επομένως, η περιοχή σύγκλισης της αρχικής σειράς είναι ένα τμήμα.

Απόφαση. Βρείτε την ακτίνα σύγκλισης της σειράς:

Επομένως, η σειρά συγκλίνει στο, δηλ. στο.

Ας πάρουμε μια σειρά , το οποίο συγκλίνει σύμφωνα με το τεστ Leibniz.

Παίρνουμε μια αποκλίνουσα σειρά

.

Επομένως, η περιοχή σύγκλισης της αρχικής σειράς είναι το διάστημα.

IV. Αποσύνθεση στοιχειώδεις λειτουργίεςστη σειρά Maclaurin.

Για τις εφαρμογές, είναι σημαντικό να είστε σε θέση αυτή τη λειτουργίαεπέκταση σε μια σειρά ισχύος, π.χ. αντιπροσωπεύουν τη συνάρτηση ως άθροισμα μιας σειράς ισχύος.

Μια σειρά Taylor για μια συνάρτηση ονομάζεται σειρά ισχύος της μορφής

Αν , τότε έχουμε μια ειδική περίπτωση της σειράς Taylor

η οποία ονομάζεται κοντά στο Maclaurin .

Μια σειρά ισχύος εντός του διαστήματος σύγκλισής της μπορεί να διαφοροποιηθεί και να ενσωματωθεί όσες φορές είναι επιθυμητό και η σειρά που προκύπτει έχει το ίδιο διάστημα σύγκλισης με την αρχική σειρά.

Δύο σειρές ισχύος μπορούν να προστεθούν και να πολλαπλασιαστούν όρο προς όρο σύμφωνα με τους κανόνες πρόσθεσης και πολλαπλασιασμού πολυωνύμων. Σε αυτήν την περίπτωση, το διάστημα σύγκλισης της νέας σειράς που προκύπτει συμπίπτει με το κοινό μέρος των διαστημάτων σύγκλισης της αρχικής σειράς.

Για να επεκτείνετε μια συνάρτηση σε μια σειρά Maclaurin, είναι απαραίτητο:

Υπολογίστε τις τιμές της συνάρτησης και των διαδοχικών παραγώγων της στο σημείο , δηλ.,,,…,;

Συνθέστε μια σειρά Maclaurin αντικαθιστώντας τις τιμές μιας συνάρτησης και των διαδοχικών παραγώγων της στον τύπο της σειράς Maclaurin.

Βρείτε το διάστημα σύγκλισης της σειράς που προκύπτει από τον τύπο

, .

Παράδειγμα 1. Αναπτύξτε μια συνάρτηση σε μια σειρά Maclaurin.

Απόφαση. Οπως και , τότε, αντικαθιστώντας με στην επέκταση, παίρνουμε:

Παράδειγμα 2. Γράψτε τη σειρά Maclaurin της συνάρτησης .

Απόφαση. Αφού , τότε χρησιμοποιώντας τον τύπο στον οποίο αντικαθιστούμε με , παίρνουμε:

,

Παράδειγμα 3. Αναπτύξτε τη συνάρτηση σε μια σειρά Maclaurin.

Απόφαση. Ας χρησιμοποιήσουμε τον τύπο. Οπως και

, στη συνέχεια αντικαθιστώντας με παίρνουμε:

, ή

όπου, δηλ. .

V. Πρακτικές εργασίες για τον αυτοέλεγχο των μαθητών.

Καθορίστε τη σύγκλιση χρησιμοποιώντας τη δοκιμή σύγκρισης σειρών

ή η απόκλιση της σειράς:

συγκλίνει υπό όρους·

συγκλίνει υπό όρους·

ταιριάζει απόλυτα.

;

;

VII. Αναφορά ιστορίας.

Η λύση πολλών προβλημάτων ανάγεται στον υπολογισμό των τιμών των συναρτήσεων και των ολοκληρωμάτων ή στη λύση διαφορικών εξισώσεων που περιέχουν παραγώγους ή διαφορικά άγνωστων συναρτήσεων.

Ωστόσο, η ακριβής εκτέλεση αυτών των μαθηματικών πράξεων σε πολλές περιπτώσεις αποδεικνύεται πολύ δύσκολη ή αδύνατη. Σε αυτές τις περιπτώσεις, είναι δυνατό να επιτευχθεί μια κατά προσέγγιση λύση πολλών προβλημάτων με οποιαδήποτε επιθυμητή ακρίβεια χρησιμοποιώντας σειρές.

Οι σειρές είναι ένα απλό και τέλειο εργαλείο μαθηματικής ανάλυσης για τον κατά προσέγγιση υπολογισμό συναρτήσεων, ολοκληρωμάτων και λύσεων διαφορικών εξισώσεων.

Και στέκεται στη δεξιά πλευρά του λειτουργικού.

Για να βάλουμε το πρόσημο του ίσου αντί του πρόσημου «», είναι απαραίτητο να διεξαχθεί κάποιος επιπλέον συλλογισμός που σχετίζεται ακριβώς με το άπειρο του αριθμού των όρων στη δεξιά πλευρά της ισότητας και που αφορά την περιοχή σύγκλισης της σειράς.

Όταν ο τύπος Taylor παίρνει τη μορφή με την οποία ονομάζεται τύπος Maclaurin:

Ο Colin Maclaurin (1698 - 1746), μαθητής του Newton, στην Πραγματεία του για τις Ροές (1742) διαπίστωσε ότι υπάρχει μόνο μία σειρά ισχύος που εκφράζει μια αναλυτική συνάρτηση, και αυτή θα είναι η σειρά Taylor που δημιουργείται από μια τέτοια συνάρτηση. Στον διωνυμικό τύπο του Newton, οι συντελεστές στις δυνάμεις είναι οι τιμές, όπου .

Έτσι, οι σειρές προέκυψαν τον 18ο αιώνα. ως τρόπο αναπαράστασης συναρτήσεων που επιτρέπουν άπειρη διαφοροποίηση. Ωστόσο, η συνάρτηση που αντιπροσωπεύεται από τη σειρά δεν ονομαζόταν το άθροισμά της και γενικά εκείνη την εποχή δεν είχε καθοριστεί ακόμη ποιο ήταν το άθροισμα μιας αριθμητικής ή συναρτησιακής σειράς, υπήρχαν μόνο προσπάθειες εισαγωγής αυτής της έννοιας.

Για παράδειγμα, ο L. Euler (1707-1783), έχοντας γράψει μια σειρά ισχύος που αντιστοιχεί σε μια συνάρτηση, έδωσε στη μεταβλητή μια συγκεκριμένη τιμή. Πήρα μια αριθμητική γραμμή. Ο Euler θεώρησε ότι η τιμή της αρχικής συνάρτησης στο σημείο είναι το άθροισμα αυτής της σειράς. Αυτό όμως δεν είναι πάντα αλήθεια.

Το γεγονός ότι η αποκλίνουσα σειρά δεν έχει άθροισμα, οι επιστήμονες άρχισαν να μαντεύουν μόνο τον 19ο αιώνα, αν και τον 18ο αιώνα. πολλοί, και κυρίως ο L. Euler, εργάστηκαν σκληρά πάνω στις έννοιες της σύγκλισης και της απόκλισης. Ο Euler ονόμασε μια σειρά συγκλίνουσα εάν ο κοινός όρος της τείνει στο μηδέν ως .

Στη θεωρία των αποκλίνων σειρών, ο Euler έλαβε πολλά σημαντικά αποτελέσματα, αλλά αυτά τα αποτελέσματα δεν βρήκαν εφαρμογή για μεγάλο χρονικό διάστημα. Πίσω στο 1826 Ν.Γ. Ο Άμπελ (1802 - 1829) αποκάλεσε τις αποκλίνουσες σειρές "διαβολική κατασκευή". Τα αποτελέσματα του Euler βρήκαν αιτιολόγηση μόνο στο τέλη XIXσε.

Στη διαμόρφωση της έννοιας του αθροίσματος μιας συγκλίνουσας σειράς, ο Γάλλος επιστήμονας O.L. Cauchy (1789 - 1857); έκανε εξαιρετικά όχι μόνο στη θεωρία των σειρών, αλλά και στη θεωρία των ορίων, στην ανάπτυξη της ίδιας της έννοιας του ορίου. Το 1826 Ο Cauchy δήλωσε ότι μια αποκλίνουσα σειρά δεν έχει άθροισμα.

Το 1768 Ο Γάλλος μαθηματικός και φιλόσοφος J.L. Ο D'Alembert μελέτησε τον λόγο του επόμενου όρου προς τον προηγούμενο στη διωνυμική σειρά και έδειξε ότι αν αυτός ο λόγος είναι μικρότερος από ένα σε απόλυτη τιμή, τότε η σειρά συγκλίνει. Ο Cauchy το 1821 απέδειξε ένα θεώρημα που δηλώνει στο γενική εικόναμια δοκιμή για τη σύγκλιση θετικών σειρών, που τώρα ονομάζεται τεστ d'Alembert.

Για τη μελέτη της σύγκλισης των εναλλασσόμενων σειρών, χρησιμοποιείται το τεστ Leibniz.

G.V. Ο Leibniz (1646 - 1716), ο μεγάλος Γερμανός μαθηματικός και φιλόσοφος, μαζί με τον I. Newton, είναι ο ιδρυτής του διαφορικού και ολοκληρωτικού λογισμού.

Βιβλιογραφία:

Κύριος:

1. Bogomolov N.V., Πρακτικά μαθήματα στα μαθηματικά. Μ., " μεταπτυχιακό σχολείο», 1990 – 495 σ.;
2. Tarasov N.P., Μάθημα ανώτερων μαθηματικών για τεχνικές σχολές. M., "Nauka", 1971 - 448 p.;
3. Zaitsev I.L., Ένα μάθημα ανώτερων μαθηματικών για τεχνικές σχολές. Μ., κρατικός εκδοτικός οίκος τεχνικών σχολών - θεωρητική λογοτεχνία, 1957 - 339 σ.;
4. Pismenny D.T., Ένα μάθημα διαλέξεων για ανώτερα μαθηματικά. Μ., “Iris Press”, 2005, part 2 – 256 p.;
5. Vygodsky M.Ya., Εγχειρίδιο ανώτερων μαθηματικών. M., "Nauka", 1975 - 872 p.;

Πρόσθετος:

1. Gusak A.A., Ανώτερα μαθηματικά. Σε 2 τόμους, Τόμος 2: Εγχειρίδιο για φοιτητές. Mos., "TetraSystems", 1988 - 448 σ.;
2. Griguletsky V.G., Lukyanova I.V., Petunina I.A., Μαθηματικά για φοιτητές οικονομικών ειδικοτήτων. Μέρος 2. Krasnodar, 2002 - 348 p.;
3. Griguletsky V.G. κλπ. Βιβλίο εργασιών στα μαθηματικά. Κρασνοντάρ. KSAU, 2003 - 170 p.;
4. Griguletsky V.G., Stepantsova K.G., Getman V.N., Εργασίες και ασκήσεις για φοιτητές σχολής λογιστικής και χρηματοοικονομικής. Κρασνοντάρ. 2001 - 173 σ.;
5. Griguletsky V.G., Yaschenko Z.V., Ανώτερα μαθηματικά. Krasnodar, 1998 - 186 p.;
6. Malykhin V.I., Μαθηματικά στα Οικονομικά. M., "Infra-M", 1999 - 356s.

Ορισμός 1.1. Ένας αριθμός δίπλα σε ένα κοινό μέλος είναι μια ακολουθία αριθμών που συνδέονται με ένα πρόσθετο πρόσημο, δηλαδή μια έκφραση της μορφής:

Αυτή η σειρά είναι επίσης γραμμένη ως

Παράδειγμα 1.1. Αν τότε η σειρά μοιάζει με:

Μερικές φορές, όταν γράφετε μια σειρά, μόνο μερικά από τα πρώτα μέλη της διαγράφονται. Αυτό γίνεται μόνο όταν φαίνεται εύκολα το μοτίβο που είναι χαρακτηριστικό των μελών της σειράς. Αυστηρά μιλώντας, αυτός ο τρόπος προσδιορισμού μιας σειράς δεν είναι μαθηματικά σωστός, αφού η απόκτηση ενός τύπου κοινού όρου για αρκετούς πρώτους όρους μιας σειράς είναι ένα πρόβλημα που δεν έχει μοναδική λύση.

Παράδειγμα 1.2. Ας γράψουμε έναν από τους πιθανούς τύπους για τον κοινό όρο της σειράς, γνωρίζοντας τους πρώτους 4 όρους της:

Απόφαση. Θεωρήστε πρώτα την ακολουθία των αριθμητών 2, 5, 8, 11. Σχηματίζουν μια αριθμητική πρόοδο, ο πρώτος όρος της οποίας είναι 2 και η διαφορά είναι 3. Αυτό επιτρέπει ως γενική έκφρασηγια τον αριθμητή, πάρτε τον τύπο του γενικού όρου αριθμητική πρόοδος: Οι παρονομαστές 2, 6, 18, 54 σχηματίζουν μια γεωμετρική πρόοδο με

Το πρώτο μέλος είναι 2 και ο παρονομαστής είναι 3. Ως γενική έκφρασή τους, μπορούμε να πάρουμε τον τύπο του κοινού όρου μιας γεωμετρικής προόδου.Έτσι, ο κοινός όρος της σειράς θα έχει την εξής μορφή:

Θα πρέπει να σημειωθεί ότι μια πιο σύνθετη έκφραση θα μπορούσε να ληφθεί ως γενικός όρος

Μπορείτε να υπολογίσετε το άθροισμα μιας σειράς μόνο εάν η σειρά συγκλίνει. Εάν η σειρά αποκλίνει, τότε το άθροισμα της σειράς είναι άπειρο και δεν έχει νόημα να υπολογίσουμε κάτι. Ακολουθούν παραδείγματα από την πρακτική εύρεσης του αθροίσματος μιας σειράς που ρωτήθηκαν στο Lviv εθνικό πανεπιστήμιοπήρε το όνομά του από τον Ιβάν Φράνκο. Οι εργασίες για τη σειρά επιλέγονται έτσι ώστε η συνθήκη σύγκλισης να ικανοποιείται πάντα, αλλά θα εκτελέσουμε μια δοκιμή σύγκλισης. Αυτό και τα ακόλουθα άρθρα αποτελούν τη λύση εργασίες ελέγχουμε ανάλυση σειρών.

Παράδειγμα 1.4 Υπολογίστε το άθροισμα των σειρών:
ένα)
Υπολογισμοί: Επειδή το όριο του κοινού όρου της σειράς στον αριθμό δίπλα στο άπειρο είναι 0

τότε η σειρά συγκλίνει. Ας υπολογίσουμε το άθροισμα της σειράς. Για να γίνει αυτό, μετασχηματίζουμε τον κοινό όρο επεκτείνοντάς τον στα απλούστερα κλάσματα του τύπου Ι και ΙΙ. Η μέθοδος επέκτασης σε απλά κλάσματα δεν θα δοθεί εδώ (περιγράφεται καλά κατά την ολοκλήρωση κλασμάτων), αλλά θα γράψουμε μόνο την τελική μορφή επέκτασης

Σύμφωνα με αυτό, μπορούμε να ζωγραφίσουμε το άθροισμα μέσω του αθροίσματος μιας σειράς που σχηματίζεται από απλά κλάσματα και στη συνέχεια από τη διαφορά στα αθροίσματα της σειράς

Στη συνέχεια, ζωγραφίζουμε κάθε σειρά σε ένα ρητό άθροισμα και επισημαίνουμε τους όρους (υπογράμμιση), οι οποίοι θα γίνουν 0 μετά την προσθήκη. Έτσι, το άθροισμα της σειράς θα απλοποιηθεί στο άθροισμα 3 όρων (που υποδεικνύεται με μαύρο), το οποίο θα έχει ως αποτέλεσμα 33/40.

Όλο το πρακτικό μέρος της εύρεσης του αθροίσματος για απλές σειρές βασίζεται σε αυτό.
Τα παραδείγματα για μιγαδικές σειρές μειώνονται στο άθροισμα των απείρως φθίνουσας προόδου και των σειρών, που βρίσκονται μέσω των αντίστοιχων τύπων, αλλά δεν θα εξετάσουμε τέτοια παραδείγματα εδώ.
σι)
Υπολογισμοί: Βρίσκοντας το όριο του ν’ όρου του αθροίσματος

Είναι ίσο με μηδέν, επομένως η δεδομένη σειρά συγκλίνει και είναι λογικό να αναζητήσουμε το άθροισμά της. Εάν το όριο είναι μη μηδενικό, τότε το άθροισμα της σειράς είναι ίσο με το άπειρο με πρόσημο συν ή πλην.
Ας βρούμε το άθροισμα της σειράς. Για να γίνει αυτό, ο κοινός όρος της σειράς, που είναι κλάσμα, μετατρέπεται με τη μέθοδο των αόριστων συντελεστών στο άθροισμα απλών κλασμάτων τύπου Ι.

Περαιτέρω, σύμφωνα με τις οδηγίες που δόθηκαν προηγουμένως, γράφουμε το άθροισμα της σειράς μέσω των αντίστοιχων αθροισμάτων απλών κλασμάτων

Ζωγραφίζουμε τα αθροίσματα και επιλέγουμε τους όρους που θα γίνουν ίσοι με 0 όταν συνοψιστούν.

Ως αποτέλεσμα, παίρνουμε το άθροισμα πολλών όρων (επισημασμένο με μαύρο χρώμα) που ισούται με 17/6.

Παράδειγμα 1.9 Βρείτε το άθροισμα μιας σειράς:
ένα)
Υπολογισμός: Υπολογίσιμο όριο

Βεβαιωνόμαστε ότι η δεδομένη σειρά συγκλίνει και μπορούμε να βρούμε το άθροισμα. Επιπλέον, ο παρονομαστής της συνάρτησης του αριθμού n αποσυντίθεται σε πρώτους παράγοντες και ολόκληρο το κλάσμα μετατρέπεται στο άθροισμα απλών κλασμάτων του τύπου Ι

Στη συνέχεια, γράφουμε το άθροισμα της σειράς σύμφωνα με το χρονοδιάγραμμα μέσω δύο απλών

Γράφουμε τη σειρά σε ρητή μορφή και επιλέγουμε τους όρους, οι οποίοι, αφού προσθέσουμε, θα αθροιστούν στο μηδέν. Οι υπόλοιποι όροι (επισημαίνονται με μαύρο χρώμα) και είναι το τελικό άθροισμα της σειράς

Έτσι, για να βρεθεί το άθροισμα της σειράς, είναι απαραίτητο στην πράξη να μειωθεί το under κοινό παρονομαστή 3 απλά κλάσματα.
σι)
Υπολογισμοί: Το όριο του όρου της σειράς τείνει στο μηδέν σε μεγάλες τιμές του αριθμού

Από αυτό προκύπτει ότι η σειρά συγκλίνει και το άθροισμά της είναι πεπερασμένο. Ας βρούμε το άθροισμα της σειράς, για αυτό, πρώτα, χρησιμοποιώντας τη μέθοδο των αόριστων συντελεστών, επεκτείνουμε τον κοινό όρο της σειράς σε τρεις απλούς τύπους

Αντίστοιχα, το άθροισμα της σειράς μπορεί να μετατραπεί σε άθροισμα τριών απλών σειρών

Στη συνέχεια, αναζητούμε τους όρους και στα τρία αθροίσματα, οι οποίοι μετά την άθροιση μετατρέπονται σε μηδέν. Σε σειρές που περιέχουν τρία απλά κλάσματα, ένα από αυτά γίνεται ίσο με μηδέν όταν αθροίζεται (επισημαίνεται με κόκκινο). Αυτό χρησιμεύει ως ένα είδος υπόδειξης στους υπολογισμούς.

Το άθροισμα της σειράς είναι ίσο με το άθροισμα 3 όρων και είναι ίσο με ένα.

Παράδειγμα 1.15 Υπολογίστε το άθροισμα της σειράς:
ένα)

Υπολογισμοί: Με τον γενικό όρο της σειράς να τείνει στο μηδέν

αυτή η σειρά συγκλίνει. Μετασχηματίζουμε τον κοινό όρο με τέτοιο τρόπο ώστε να έχουμε το άθροισμα των απλών κλασμάτων

Επιπλέον, η δεδομένη σειρά, σύμφωνα με τους τύπους χρονοδιαγράμματος, γράφεται μέσω του αθροίσματος δύο σειρών

Αφού γράψετε σε ρητή μορφή, οι περισσότεροι από τους όρους της σειράς θα γίνουν ίσοι με το μηδέν ως αποτέλεσμα της άθροισης. Απομένει να υπολογίσουμε το άθροισμα τριών όρων.

Το άθροισμα της σειράς αριθμών είναι -1/30.
σι)
Υπολογισμοί: Εφόσον το όριο του κοινού όρου της σειράς είναι μηδέν,

τότε η σειρά συγκλίνει. Για να βρούμε το άθροισμα της σειράς, επεκτείνουμε τον κοινό όρο σε κλάσματα του απλούστερου τύπου.

Στην αποσύνθεση χρησιμοποιήθηκε η μέθοδος των απροσδιόριστων συντελεστών. Καταγράφουμε το άθροισμα της σειράς από το πρόγραμμα που βρέθηκε

Το επόμενο βήμα είναι να επιλέξετε τους όρους που δεν συνεισφέρουν στο τελικό άθροισμα και τους υπόλοιπους

Το άθροισμα της σειράς είναι 4,5.

Παράδειγμα 1.25 Υπολογίστε το άθροισμα των σειρών:
ένα)


Εφόσον ισούται με μηδέν, η σειρά συγκλίνει. Μπορούμε να βρούμε το άθροισμα της σειράς. Για να γίνει αυτό, σύμφωνα με το σχήμα των προηγούμενων παραδειγμάτων, επεκτείνουμε τον κοινό όρο της σειράς μέσω απλών κλασμάτων

Αυτό σας επιτρέπει να γράψετε μια σειρά μέσω του αθροίσματος απλών σειρών και, επισημαίνοντας τους όρους σε αυτήν, απλοποιώντας την άθροιση.

Σε αυτή την περίπτωση, θα υπάρχει ένας όρος που ισούται με έναν.
σι)
Υπολογισμοί: Βρείτε το όριο του κοινού όρου της σειράς

και βεβαιωθείτε ότι η σειρά συγκλίνει. Περαιτέρω, ο κοινός όρος της σειράς αριθμών διασπάται με τη μέθοδο των αόριστων συντελεστών σε κλάσματα του απλούστερου τύπου.

Μέσα από τα ίδια κλάσματα ζωγραφίζουμε το άθροισμα της σειράς

Γράφουμε τη σειρά σε ρητή μορφή και απλοποιούμε στο άθροισμα 3 όρων

Το άθροισμα της σειράς είναι 1/4.
Αυτό ολοκληρώνει την εισαγωγή στα σχήματα άθροισης σειρών. Εδώ, οι σειρές δεν έχουν ακόμη ληφθεί υπόψη, οι οποίες μειώνονται στο άθροισμα μιας απείρως φθίνουσας γεωμετρικής προόδου, που περιέχει παραγοντικούς, εξαρτήσεις ισχύος και παρόμοια. Ωστόσο, το υλικό που παρουσιάζεται θα είναι χρήσιμο για τους μαθητές στον έλεγχο και τα τεστ.

Αριθμητικές γραμμές. Σύγκλιση και απόκλιση αριθμητικών σειρών. Δοκιμή σύγκλισης d'Alembert. Μεταβλητές σειρές. Απόλυτη και υπό όρους σύγκλιση σειρών. λειτουργικές σειρές. Power σειρά. Επέκταση στοιχειωδών συναρτήσεων στη σειρά Maclaurin.

Κατευθυντήριες γραμμέςστο θέμα 1.4:

Αριθμητικές σειρές:

Μια σειρά αριθμών είναι ένα άθροισμα της φόρμας

που είναι οι αριθμοί u 1 , u 2 , u 3 , n n ,που ονομάζονται μέλη της σειράς, σχηματίζουν μια άπειρη ακολουθία. ο όρος un ονομάζεται κοινός όρος της σειράς.

. . . . . . . . .

που αποτελούνται από τους πρώτους όρους της σειράς (27.1) ονομάζονται επιμέρους αθροίσματα αυτής της σειράς.

Κάθε σειρά μπορεί να συσχετιστεί με μια ακολουθία μερικών αθροισμάτων S1, S2, S3. Αν, καθώς ο αριθμός n αυξάνεται άπειρα, το μερικό άθροισμα της σειράς S nτείνει στο όριο μικρό, τότε η σειρά ονομάζεται συγκλίνουσα και ο αριθμός ΜΙΚΡΟ-το άθροισμα μιας συγκλίνουσας σειράς, δηλ.

Αυτή η καταχώρηση είναι ισοδύναμη με την καταχώρηση

Εάν ένα μερικό ποσό S nσειρά (27.1) με απεριόριστη αύξηση nδεν έχει πεπερασμένο όριο (ιδίως, τείνει στο + ¥ ή στο - ¥), τότε μια τέτοια σειρά ονομάζεται αποκλίνουσα

Εάν η σειρά συγκλίνει, τότε η τιμή S nγια αρκετά μεγάλο n είναι μια κατά προσέγγιση έκφραση για το άθροισμα της σειράς μικρό.

Διαφορά r n = S - S nονομάζεται το υπόλοιπο της σειράς. Εάν η σειρά συγκλίνει, τότε το υπόλοιπο της τείνει στο μηδέν, δηλ. r n = 0, και αντίστροφα, αν το υπόλοιπο τείνει στο μηδέν, τότε η σειρά συγκλίνει.

Η σειρά ενός είδους ονομάζεται γεωμετρική γραμμή.

που ονομάζεται αρμονικός.

αν Ν®¥, λοιπόν S n®¥, δηλ. η αρμονική σειρά αποκλίνει.

Παράδειγμα 1. Γράψτε μια σειρά με τον δεδομένο κοινό όρο της:

1) υποθέτοντας n = 1, n = 2, n = 3, έχουμε μια άπειρη ακολουθία αριθμών: , , , Προσθέτοντας τους όρους της, παίρνουμε τη σειρά

2) Κάνοντας το ίδιο, παίρνουμε τη σειρά

3) Δίνοντας n τις τιμές 1, 2, 3, και λαμβάνοντας υπόψη ότι 1! = 1, 2! = 1 × 2, 3! = 1 × 2 × 3, παίρνουμε τη σειρά

Παράδειγμα 2. Βρείτε n-ο όρος της σειράς με τους δοσμένους πρώτους αριθμούς:

1) ; 2) ; 3) .

Παράδειγμα 3. Βρείτε το άθροισμα των όρων της σειράς:

1) Βρείτε τα επιμέρους αθροίσματα των όρων της σειράς:

Ας γράψουμε την ακολουθία των μερικών αθροισμάτων: …, , ….

Ο κοινός όρος αυτής της ακολουθίας είναι . Ως εκ τούτου,

Η ακολουθία των μερικών αθροισμάτων έχει όριο ίσο με . Άρα η σειρά συγκλίνει και το άθροισμά της είναι .

2) Αυτό είναι απείρως φθίνουσα γεωμετρική πρόοδος, όπου a 1 = , q= . Χρησιμοποιώντας τον τύπο, παίρνουμε Άρα, η σειρά συγκλίνει και το άθροισμά της είναι ίσο με 1.

Σύγκλιση και απόκλιση αριθμητικών σειρών. Σημάδι σύγκλισης d'Alembert :

Απαραίτητο κριτήριο για τη σύγκλιση μιας σειράς.Μια σειρά μπορεί να συγκλίνει μόνο αν ο κοινός όρος της είναι u n με απεριόριστη αύξηση αριθμού nπάει στο μηδέν:

Εάν , τότε η σειρά αποκλίνει - αυτό είναι επαρκές σημάδι της διαλυτότητας της σειράς.

Επαρκείς προϋποθέσεις για τη σύγκλιση μιας σειράς με θετικούς όρους.

Σημάδι σύγκρισης σειρών με θετικούς όρους. Η υπό μελέτη σειρά συγκλίνει εάν τα μέλη της δεν υπερβαίνουν τα αντίστοιχα μέλη μιας άλλης, προφανώς συγκλίνουσας σειράς. η υπό μελέτη σειρά αποκλίνει εάν οι όροι της υπερβαίνουν τους αντίστοιχους όρους μιας άλλης εμφανώς αποκλίνουσας σειράς.

Στη μελέτη σειρών για σύγκλιση και διαλυτότητα σε αυτή τη βάση, χρησιμοποιείται συχνά η γεωμετρική σειρά

που συγκλίνει για |q|

όντας αποκλίνουσα.

Στη μελέτη σειρών χρησιμοποιείται και η γενικευμένη αρμονική σειρά

Αν ένα Π= 1, τότε αυτή η σειρά μετατρέπεται σε αρμονική σειρά, η οποία είναι αποκλίνουσα.

Αν ένα Π< 1, то члены данного ряда больше соответствующих членов гармонического ряда и, значит, он расходится. При Π> 1 έχουμε μια γεωμετρική σειρά στην οποία | q| < 1; он является сходящимся. Итак, обобщенный гармонический ряд сходится при Π> 1 και αποκλίνει στο Π£1.

Σημάδι του d'Alembert. Αν για μια σειρά με θετικούς όρους

(u n>0)

η συνθήκη ικανοποιείται, τότε η σειρά συγκλίνει στο μεγάλο l > 1.

Το σημάδι του d'Alembert δεν δίνει απάντηση αν μεγάλο= 1. Σε αυτή την περίπτωση, χρησιμοποιούνται άλλες μέθοδοι για τη μελέτη της σειράς.

Μεταβλητές σειρές.

Απόλυτη και υπό όρους σύγκλιση σειρών:

Σειρά αριθμών

u 1 + u 2 + u 3 + u n

ονομάζεται εναλλασσόμενος εάν μεταξύ των μελών του υπάρχουν και θετικοί και αρνητικοί αριθμοί.

Μια σειρά αριθμών ονομάζεται εναλλασσόμενη πρόσημο εάν δύο γειτονικά μέλη έχουν αντίθετα πρόσημα. Αυτή η σειρά είναι μια ειδική περίπτωση μιας εναλλασσόμενης σειράς.

Κριτήριο σύγκλισης για εναλλασσόμενες σειρές. Αν οι όροι της εναλλασσόμενης σειράς μειώνονται μονοτονικά σε απόλυτη τιμή και ο κοινός όρος uΤο n τείνει στο μηδέν ως n® , τότε η σειρά συγκλίνει.

Μια σειρά ονομάζεται απολύτως συγκλίνουσα αν η σειρά συγκλίνει επίσης. Εάν μια σειρά συγκλίνει απόλυτα, τότε είναι συγκλίνουσα (με τη συνήθη έννοια). Το αντίστροφο δεν είναι αλήθεια. Μια σειρά λέγεται ότι είναι υπό όρους σύγκλιση εάν η ίδια συγκλίνει και η σειρά που αποτελείται από τις ενότητες των μελών της αποκλίνει. Παράδειγμα 4. Εξετάστε τη σειρά για σύγκλιση.

Ας εφαρμόσουμε την επαρκή δοκιμή Leibniz για εναλλασσόμενες σειρές. Παίρνουμε γιατί . Επομένως, αυτή η σειρά συγκλίνει. Παράδειγμα 5. Εξετάστε τη σειρά για σύγκλιση.

Ας προσπαθήσουμε να εφαρμόσουμε το πρόσημο Leibniz: Μπορεί να φανεί ότι το μέτρο του κοινού όρου δεν τείνει στο μηδέν όταν n→∞. Επομένως, αυτή η σειρά αποκλίνει. Παράδειγμα 6. Προσδιορίστε εάν η σειρά είναι απολύτως συγκλίνουσα, υπό όρους συγκλίνουσα ή αποκλίνουσα.

Εφαρμόζοντας το τεστ d'Alembert σε μια σειρά που αποτελείται από τις ενότητες των αντίστοιχων όρων, βρίσκουμε Επομένως, αυτή η σειρά συγκλίνει απόλυτα.

Παράδειγμα 7. Εξετάστε για σύγκλιση (απόλυτη ή υπό όρους) μια εναλλασσόμενη σειρά:

1) Οι όροι αυτής της σειράς μειώνονται μονότονα σε απόλυτη τιμή και . Επομένως, σύμφωνα με το τεστ Leibniz, η σειρά συγκλίνει. Ας μάθουμε αν αυτή η σειρά συγκλίνει απολύτως ή υπό όρους.

2) Οι όροι αυτής της σειράς μειώνονται μονότονα σε απόλυτη τιμή: , αλλά

Λειτουργική σειρά:

Η συνηθισμένη σειρά αριθμών αποτελείται από αριθμούς:

Όλα τα μέλη της σειράς είναι αριθμοί.

Η λειτουργική γραμμή αποτελείται από χαρακτηριστικά:

Στον γενικό όρο της σειράς, εκτός από πολυώνυμα, παραγοντικά κ.λπ. σίγουραπεριλαμβάνει το γράμμα «x». Μοιάζει με αυτό, για παράδειγμα: Όπως μια σειρά αριθμών, κάθε λειτουργική σειρά μπορεί να γραφτεί σε διευρυμένη μορφή:

Όπως μπορείτε να δείτε, όλα τα μέλη της λειτουργικής σειράς είναι λειτουργίες.

Ο πιο δημοφιλής τύπος λειτουργικής σειράς είναι σειρά ισχύος.

Power σειρά:

δύναμη στη συνέχειαονομάζεται σειρά

που είναι οι αριθμοί a 0, a 1, a 2, a nλέγονται οι συντελεστές της σειράς, και ο όρος a n x nείναι κοινό μέλος της σειράς.

Η περιοχή σύγκλισης μιας σειράς ισχύος είναι το σύνολο όλων των τιμών Χγια την οποία η σειρά συγκλίνει.

Αριθμός Rονομάζεται ακτίνα σύγκλισης της σειράς εάν, για | x| η σειρά συγκλίνει.

Παράδειγμα 8. Δίνεται μια σειρά

Διερευνήστε τη σύγκλιση σε σημεία Χ= 1 και Χ= 3, Χ= -2.

Όταν x = 1, αυτή η σειρά μετατρέπεται σε σειρά αριθμών

Ας διερευνήσουμε τη σύγκλιση αυτής της σειράς με το τεστ d'Alembert. Εχουμε

Εκείνοι. η σειρά συγκλίνει.

Για x = 3 παίρνουμε τη σειρά

Το οποίο αποκλίνει, αφού δεν ικανοποιείται το απαραίτητο κριτήριο για τη σύγκλιση της σειράς

Για x = -2 παίρνουμε

Πρόκειται για μια εναλλασσόμενη σειρά, η οποία, σύμφωνα με το τεστ Leibniz, συγκλίνει.

Στα σημεία λοιπόν Χ= 1 και Χ= -2. η σειρά συγκλίνει, και στο σημείο Χ= 3 αποκλίνει.

Επέκταση στοιχειωδών συναρτήσεων στη σειρά Maclaurin:

Κοντά στο Taylorγια λειτουργία f(x)ονομάζεται σειρά ισχύος της μορφής

Αν ένα, α = 0, τότε έχουμε μια ειδική περίπτωση της σειράς Taylor

η οποία ονομάζεται δίπλα στον Maclaurin.

Μια σειρά ισχύος εντός του διαστήματος σύγκλισής της μπορεί να διαφοροποιηθεί και να ενσωματωθεί όσες φορές είναι επιθυμητό και η σειρά που προκύπτει έχει το ίδιο διάστημα σύγκλισης με την αρχική σειρά.

Δύο σειρές ισχύος μπορούν να προστεθούν και να πολλαπλασιαστούν όρο προς όρο σύμφωνα με τους κανόνες πρόσθεσης και πολλαπλασιασμού πολυωνύμων. Σε αυτήν την περίπτωση, το διάστημα σύγκλισης της νέας σειράς που προκύπτει συμπίπτει με το κοινό μέρος των διαστημάτων σύγκλισης της αρχικής σειράς.

Για να επεκτείνετε μια συνάρτηση σε μια σειρά Maclaurin, είναι απαραίτητο:

1) υπολογίστε τις τιμές της συνάρτησης και των διαδοχικών παραγώγων της στο σημείο x= 0, δηλ. , , .

8. Αναπτύξτε τη σειρά συναρτήσεων Maclaurin.

Κάντε έναν προκαταρκτικό έλεγχο.Υπάρχει ένα απλό θεώρημα που λέει ότι αν το άπειρο άθροισμα μιας συνάρτησης f συγκλίνει, τότε το όριο της συνάρτησης f είναι ίσο με 0. Έτσι, αν έχουμε συνάρτηση x^2, τότε δεν έχει όριο και το άθροισμά της αποκλίνει στο άπειρο. από την άλλη, το όριο της συνάρτησης 1/x είναι 0, άρα το άθροισμά της μπορεί να συγκλίνει. Εάν το όριο είναι μη μηδενικό, γνωρίζουμε ότι η σειρά αποκλίνει. ΠΡΟΣΟΧΗ: δεν ισχύει το αντίστροφο, δηλαδή το ότι το όριο είναι μηδέν δεν σημαίνει καθόλου ότι η σειρά συγκλίνει απαραίτητα. Σε αυτή την περίπτωση, απαιτείται περαιτέρω έλεγχος.

γεωμετρικές σειρές.Υπάρχει ένας πολύ απλός κανόνας για αυτές τις σειρές, οπότε πρώτα καθορίστε εάν η σειρά σας δεν είναι γεωμετρική σειρά. Μια γεωμετρική σειρά είναι μια ακολουθία αριθμών, κάθε όρος των οποίων μπορεί να αναπαρασταθεί ως r^k, όπου k είναι μια μεταβλητή και r είναι ένας αριθμός μεταξύ -1 και 1. Οι γεωμετρικές σειρές συγκλίνουν πάντα. Επιπλέον, μπορείτε εύκολα να προσδιορίσετε το άθροισμα μιας τέτοιας σειράς, το οποίο είναι ίσο με 1/(1-r).

Γενικευμένη αρμονική σειρά, ή σειρά Dirichlet.Μια τέτοια σειρά είναι το άθροισμα των συναρτήσεων της μορφής 1/(x^p), όπου x είναι οποιοσδήποτε αριθμός. Το θεώρημα για αυτές τις σειρές λέει ότι αν το p είναι μεγαλύτερο από ένα, η σειρά συγκλίνει· εάν το p είναι μικρότερο ή ίσο με ένα, η σειρά αποκλίνει. Αυτό σημαίνει ότι η σειρά 1/x που αναφέρεται παραπάνω αποκλίνει επειδή μπορεί να αναπαρασταθεί ως 1/(x^1), όπου p=1. Αυτή η σειρά ονομάζεται αρμονική. Η σειρά 1/(X^2) συγκλίνει επειδή το 2 είναι μεγαλύτερο από το 1.

Άλλες σειρές.Εάν η σειρά δεν ανήκει σε έναν από τους παραπάνω τύπους, εφαρμόστε τις παρακάτω μεθόδους σε αυτήν. Εάν μια μέθοδος δεν βοηθά, δοκιμάστε την επόμενη, καθώς δεν είναι πάντα ξεκάθαρο ποια να επιλέξετε. Αν και δεν υπάρχουν σαφείς κανόνες, με την πάροδο του χρόνου θα μπορείτε να πλοηγηθείτε καλύτερα στην επιλογή της επιθυμητής μεθόδου.

• μέθοδος σύγκρισης. Ας υποθέσουμε ότι έχετε δύο θετικές σειρές, a(n) και b(n). Τότε: 1) αν το άπειρο άθροισμα b(n) συγκλίνει και το a(n) είναι μικρότερο από b(n) (για οποιοδήποτε αρκετά μεγάλο n), τότε το άθροισμα a(n) συγκλίνει επίσης. 2) αν το b(n) αποκλίνει και το a(n)>b(n), τότε το a(n) αποκλίνει επίσης. Για παράδειγμα, έχετε μια σειρά 2/x. μπορούμε να το συγκρίνουμε με τη σειρά 1/x. Εφόσον γνωρίζουμε ήδη ότι η σειρά 1/x αποκλίνει και 2/x > 1/x, προκύπτει ότι η σειρά 2/x αποκλίνει επίσης. Έτσι, η ιδέα της μεθόδου είναι να προσδιορίσει εάν η υπό μελέτη σειρά συγκλίνει ή όχι, χρησιμοποιώντας μια ήδη γνωστή σειρά.
• Μέθοδος σύγκρισης ορίων. Αν τα a(n) και b(n) είναι σειρές θετικών αριθμών και αν υπάρχει όριο a(n)/b(n) που είναι μεγαλύτερο από 0, τότε και οι δύο σειρές είτε συγκλίνουν είτε αποκλίνουν. Σε αυτή την περίπτωση, η υπό μελέτη σειρά συγκρίνεται επίσης με τη γνωστή. η μέθοδος είναι να επιλέξετε μια γνωστή σειρά της οποίας ο μέγιστος βαθμός αντιστοιχεί στον βαθμό της υπό μελέτη σειράς. Για παράδειγμα, αν σκέφτεστε τη σειρά 1/(x^3+2x+1), είναι λογικό να τη συγκρίνετε με τη σειρά 1/(x^3).
• Ολοκληρωμένος έλεγχος. Εάν η συνάρτηση είναι μεγαλύτερη από το μηδέν, συνεχής και φθίνουσα για τιμές x μεγαλύτερες ή ίσες με 1, τότε η άπειρη σειρά f(n) συγκλίνει εάν οριστικό ολοκλήρωμααπό το 1 έως το άπειρο από τη συνάρτηση f(x) υπάρχει και έχει πεπερασμένη τιμή. διαφορετικά, η σειρά αποκλίνει. Έτσι, αρκεί να ενσωματώσουμε τη συνάρτηση και να βρούμε το όριο καθώς το x τείνει στο άπειρο: εάν το όριο είναι πεπερασμένο, η σειρά συγκλίνει· εάν το όριο είναι άπειρο, η σειρά αποκλίνει.
• Μεταβλητές σειρές. Αν a(k)>a(k+1)>0 για αρκετά μεγάλο k, και το όριο του a(n) είναι 0, τότε η εναλλασσόμενη σειρά (-1)^n a(n) συγκλίνει. Με απλά λόγια, ας πούμε ότι η σειρά σας εναλλάσσεται (δηλαδή οι όροι της είναι εναλλάξ θετικοί και αρνητικοί). Σε αυτήν την περίπτωση, αποθέστε το εναλλασσόμενο τμήμα της συνάρτησης και βρείτε το όριο αυτού που απομένει -- εάν το όριο είναι πεπερασμένο, η σειρά συγκλίνει.
• μέθοδος σχέσης. Με δεδομένη μια άπειρη σειρά a(n), βρείτε τον επόμενο όρο της σειράς a(n+1). Στη συνέχεια, υπολογίστε την αναλογία του επόμενου όρου προς τον προηγούμενο a(n+1)/a(n), λαμβάνοντας τον εάν είναι απαραίτητο απόλυτη τιμή. Βρείτε το όριο αυτού του λόγου καθώς το n τείνει στο άπειρο. Εάν αυτό το όριο υπάρχει και είναι πεπερασμένο, αυτό σημαίνει τα εξής: 1) εάν το όριο είναι μικρότερο από ένα, η σειρά συγκλίνει. 2) εάν το όριο είναι μεγαλύτερο από ένα, η σειρά αποκλίνει. 3) εάν το όριο είναι ίσο με ένα, αυτή η μέθοδος είναι ανεπαρκής (η σειρά μπορεί και να συγκλίνει και να αποκλίνει).
• Αυτές είναι οι βασικές μέθοδοι για τον προσδιορισμό της σύγκλισης σειρών και είναι εξαιρετικά χρήσιμες. Εάν κανένα από αυτά δεν βοήθησε, είναι πιθανό το πρόβλημα να μην έχει λύση ή να κάνατε λάθος κάπου. Αυτές οι μέθοδοι μπορούν να χρησιμοποιηθούν και για άλλες σειρές, όπως π.χ σειρά ισχύος, σειρά Taylor, κ.λπ. Είναι δύσκολο να υπερεκτιμηθεί η γνώση αυτών των μεθόδων, αφού άλλες απλούς τρόπουςγια τον προσδιορισμό της σύγκλισης της σειράς δεν υπάρχει.