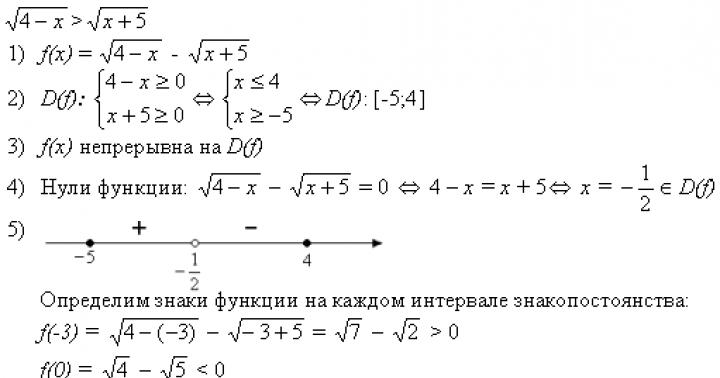grad de număr A cu un indicator natural n, mai mare decât 1, se numește produs n multiplicatori, fiecare dintre care este egal cu A:

În expresia a n:

Număr A(factor de repetare) se numește baza gradului

Număr n(care arată de câte ori se repetă multiplicatorul) - exponent

De exemplu:
2 5 = 2 2 2 2 2 = 32,
Aici:
2 - baza gradului,
5 - exponent,
32 - valoare de grade

Rețineți că baza gradului poate fi orice număr.

Calculul valorii puterii se numește acțiune de exponențiere. Aceasta este a treia etapă de acțiune. Adică, atunci când se calculează valoarea unei expresii care nu conține paranteze, se execută mai întâi acțiunea celei de-a treia etape, apoi a doua (înmulțire și împărțire) și, în final, prima (adunare și scădere).

Pentru a scrie numere mari, se folosesc adesea puteri de 10. Deci, distanța de la Pământ la Soare, aproximativ egală cu 150 de milioane de km, se scrie ca 1,5 10 8

Orice număr mai mare de 10 poate fi scris ca: a 10 n , unde 1 ≤ a< 10 и n – натуральное число. Такая запись называется стандартным видом числа.

De exemplu: 4578 \u003d 4,578 10 3;

103000 = 1,03 10 5 .

Proprietăți ale unui grad cu un indicator natural:

unu . La înmulțirea puterilor cu aceeași bază, baza rămâne aceeași, iar exponenții se adună

a m a n = a m + n

de exemplu: 7 1.7 7 - 0.9 = 7 1.7+(- 0.9) = 7 1.7 - 0.9 = 7 0.8

2. La împărțirea gradelor cu aceeași bază, baza rămâne aceeași și se scad exponenții

a m / a n = a m - n ,

unde, m > n,
a ≠ 0

ex: 13 3,8 / 13 -0,2 = 13 (3,8 -0,2) = 13 3,6

3 . La exponentiare baza rămâne aceeași, dar exponenții sunt înmulțiți.

(a m) n = a m n

de exemplu: (2 3) 2 = 2 3 2 = 2 6

patru . La exponentiarea unui produs fiecare factor este ridicat la această putere

(a b) n = a n b m ,

de exemplu: (2 3) 3 = 2 n 3 m ,

5 . La exponentiarea unei fractii numărătorul și numitorul sunt ridicate la această putere

(a / b) n = a n / b n

de exemplu: (2 / 5) 3 = (2 / 5) (2 / 5) (2 / 5) = 2 3 / 5 3

Gradul cu exponent rațional

Gradul a > 0 c indicator rațional, unde m este un număr întreg și n este un număr natural (n > 1), se numește număr

De exemplu:

Puterea lui 0 este definită numai pentru exponenții pozitivi;

prin definiție 0 r = 0 , pentru orice r > 0

Observatii

Pentru grade cu un exponent rațional, principalul proprietăți de grad , valabil pentru orice indicator (cu condiția ca baza gradului să fie pozitivă).

Gradul cu exponent real

Deci, pentru orice număr real, am definit operația de ridicare la o putere naturală; pentru orice număr, am definit exponențiații la puteri întregi negative și zero; pentru oricare, am definit operația de ridicare la o putere fracțională pozitivă; pentru oricare, am definit operația de ridicare la o putere fracțională negativă.

Se ridică o întrebare firească: este posibil să se definească în vreun fel operația de ridicare la o putere irațională și, în consecință, să se determine sensul expresiei a x pentru orice număr real x? Rezultă că pentru numerele pozitive a se poate da sensul scrierii a α , unde α este un număr irațional. Pentru a face acest lucru, trebuie să luăm în considerare trei cazuri: a = 1, a > 1, 0< a < 1.

Deci, pentru a > 0, am definit gradul cu orice exponent real.

S. Shestakov,
Moscova

Un examen scris

Clasa a 11a
1. Calcule. Conversia expresiei

§ 3. Gradul cu exponent real

Exercițiile din § 5 al primului capitol al colecției sunt legate în principal de funcția exponențială și de proprietățile acesteia. În acest paragraf, ca și în cele precedente, este testată nu doar capacitatea de a efectua transformări pe baza proprietăților cunoscute, ci și stăpânirea de către elevi a simbolurilor funcționale. Dintre sarcinile colecției, se pot distinge următoarele grupuri:

• exerciții de definire functie exponentiala(1.5.A06, 1.5.B01–B04) și capacitatea de a utiliza simboluri funcționale (1.5A02, 1.5.B05, ​​​​1.5C11);
• exercitii pentru conversia expresiei, care conține un grad cu un exponent real și pentru calcularea valorilor unor astfel de expresii și a valorilor funcției exponențiale (1.5B07, 1.5B09, 1.5.C02, 1.5.C04, 1.5.C05, 1.5D03, 1.5D05, 1.5.D10 etc.);
• exerciții de comparație valori de expresie, care conține un grad cu exponent real, necesitând utilizarea proprietăților unui grad cu exponent real și o funcție exponențială (1.5.B11, 1.5C01, 1.5C12, 1.5D01, 1.5D11);
• alte exerciții (inclusiv cele legate de notarea pozițională a numerelor, progresii etc.) - 1.5.A03, 1.5.B08, 1.5.C06, 1.5. C09, 1.5.C10, 1.5.D07, 1.5.D09.

Luați în considerare o serie de sarcini legate de simbolismul funcțional.

1.5.A02. e) Sunt date funcții

Aflați valoarea expresiei f 2 (x) - g 2 (x).

Soluţie. Să folosim formula diferenței de pătrate:

Răspuns: -12.

1.5.C11. b) Sunt date funcţii

Aflați valoarea expresiei f(x) f(y) - g(x) g(y) dacă f(x - y) = 9.

Să aducem solutii scurte exerciții de transformare a expresiilor care conțin un grad cu exponent real și de calculare a valorilor unor astfel de expresii și a valorilor funcției exponențiale.

1.5.B07. a) Se știe că 6 A – 6 –A= 6. Aflați valoarea expresiei (6 A– 6) 6 A .

Soluţie. Din condițiile problemei rezultă că 6 A – 6 = 6 -A. Apoi

(6 A– 6) 6a = 6 -A 6 A = 1.

1.5.C05. b) Aflați valoarea expresiei 7 a-b, dacă

Soluţie. După condiție Împărțiți numărătorul și numitorul din stânga acestei ecuații la 7 b . obține

Să facem un înlocuitor. Fie y = 7 a-b. Egalitatea ia forma

Rezolvăm ecuația rezultată

Următorul grup de exerciții sunt sarcini de comparare a valorilor expresiilor care conțin un grad cu un exponent real, necesitând utilizarea proprietăților unui grad cu un exponent real și o funcție exponențială.

1.5.B11. b) Aranjați numerele f(60), g(45) și h(30) în ordine descrescătoare dacă f(x) = 5 x , g(x) = 7 x și h(x) = 3 x .

Soluţie. f(60) = 5 60 , g(45) = 7 45 și h(30) = 3 30 .

Să transformăm aceste grade astfel încât să obținem aceiași indicatori:

5 60 =625 15 , 7 45 =343 15 , 3 30 =9 15 .

Să scriem bazele în ordine descrescătoare: 625 > 343 > 9.

Prin urmare, ordinea cerută este: f(60), g(45), h(30).

Răspuns: f(60), g(45), h(30).

1.5.C12. a) Comparați , unde x și y sunt numere reale.

Soluţie.

De aceea

De aceea

Deoarece 3 2 > 2 3 , obținem asta

Răspuns:

1.5.D11. a) Comparați numerele

De când primim

Răspuns:

La finalul revizuirii sarcinilor pentru o diplomă cu indicator real, vom avea în vedere exerciții legate de notarea pozițională a unui număr, progresii etc.

1.5.A03. b) Având în vedere o funcție f(x) = (0,1) x . Aflați valoarea expresiei 6f(3) + 9f(2) + 4f(1) + 4f(0).

4f(0) + 4f(1) + 9f(2) + 6f(3) = 4 1 + 4 0,1 + 9 0,01 + 6 0,001 = 4,496.

Astfel, această expresie este expansiunea în suma unităților de cifre ale fracției zecimale 4,496.

Răspuns: 4.496.

1.5.D07. a) Este dată funcția f(x) = 0,1 x. Aflați valoarea expresiei f 3 (1) - f 3 (2) + f 3 (3) + ... + (-1) n-1 f 3 (n) + ...

f 3 (1)–f 3 (2)+f 3 (3)+...+(–1) n–1 f 3 (n)+...= 0,1 3 –0,1 6 +0 ,1 9 + ...+(–1) n–1 0,1 3n + ...

Această expresie este suma unui infinit descrescător progresie geometrică cu primul termen 0,001 și numitorul -0,001. Suma este

1.5.D09. a) Aflați valoarea expresiei 5 2x +5 2y +2 5x 5 y – 25 y 5 x dacă 5 x –5 y =3, x + y = 3.

5 2x +5 2y +25 x 5 y –25 y 5 x =(5 x – 5 y) 2 +2 5 x 5 y +5 x 5 y (5 x – 5 y)=3 2 +2 5 x+ y +5 x+y 3=3 2 +2 5 3 +3 5 3 =634.

Răspuns: 634.

§ 4. Expresii logaritmice

Când se repetă subiectul „Transformarea expresiilor logaritmice” (§ 1.6 al colecției), ar trebui să ne amintim o serie de formule de bază legate de logaritmi:

Iată o serie de formule, a căror cunoaștere nu este necesară pentru a rezolva probleme de nivelurile A și B, dar pot fi utile în rezolvarea unor probleme mai complexe (numărul acestor formule poate fi fie redus, fie crescut în funcție de punctele de vedere ale profesor și nivelul de pregătire al elevilor):

Majoritatea exercițiilor de la § 1.6 din colecție pot fi atribuite uneia dintre următoarele grupuri:

• exerciții privind utilizarea directă a definiției și proprietăților logaritmilor (1.6.A03, 1.6.A04, 1.6.B01, 1.6.B05, ​​​​​1.6.B08, 1.6.B10, 1.6.C09, 1.6.D01, 1.6.D08). , 1.6.D10);
• exerciţii pentru calcularea valorii unei expresii logaritmice prin valoare dată altă expresie sau logaritm (1.6.C02, 1.6.C09, 1.6.D02);
• exerciții de comparare a valorilor a două expresii care conțin logaritmi (1.6.C11);
• exerciții cu o sarcină complexă în mai multe etape (1.6.D11, 1.6.D12).

Iată soluții scurte la exerciții privind utilizarea directă a definiției și proprietăților logaritmilor.

1.6.B05. a) Aflați valoarea expresiei

Soluţie.

Expresia ia forma

1.6.D08. b) Aflați valoarea expresiei (1 - log 4 36)(1 - log 9 36).

Soluţie. Să folosim proprietățile logaritmilor:

(1 - log 4 36)(1 - log 9 36) =

= (1 – log 4 4 – log 4 9)(1 – log 9 4 – log 9 9) =

= –log 4 9 (–log 9 4) = 1.

1.6.D10. a) Aflați valoarea expresiei

Soluţie. Să transformăm numărătorul:

log 6 42 log 7 42=(1 + log 6 7)(1 + log 7 6)=1 + log 6 7 + log 7 6 + log 6 7 log 7 6.

Dar log 6 7 log 7 6 = 1. Deci numărătorul este 2 + log 6 7 + log 7 6 și fracția este 1.

Să trecem la rezolvarea exercițiilor pentru calcularea valorii unei expresii logaritmice având în vedere valoarea unei alte expresii sau logaritm.

1.6.D02. a) Aflați valoarea expresiei log 70 320 dacă log 5 7= A, log 7 2= b.

Soluţie. Să transformăm expresia. Să trecem la baza 7:

Din condiţia rezultă că . De aceea

Următoarea problemă necesită să comparați valorile a două expresii care conțin logaritmi.

1.6.C11. a) Comparați numerele

Soluţie. Să luăm ambii logaritmi la baza 2.

Prin urmare, aceste numere sunt egale.

Răspuns: aceste numere sunt egale.

Pentru orice unghi α astfel încât α ≠ πk/2 (k aparține mulțimii Z), avem:

Pentru orice unghi α, egalitățile sunt adevărate:

Pentru orice unghi α astfel încât α ≠ πk (k aparține mulțimii Z), avem:

Formule turnate

Tabelul conține formule de reducere pentru funcțiile trigonometrice.

Funcție (unghi în º)	90º - α	90º + α	180º - α	180º + α	270º - α	270º + α	360º - α	360º + α
păcat	cosα	cosα	sinα	-sinα	-cos α	-cos α	-sinα	sinα
cos	sinα	-sinα	-cos α	-cos α	-sinα	sinα	cosα	cosα
tg	ctgα	-ctgα	-tgα	tgα	ctgα	-ctgα	-tgα	tgα
ctg	tgα	-tgα	-ctgα	ctgα	tgα	-tgα	-ctgα	ctgα
Funcție (unghi în rad.)	π/2 – α	π/2 + α	π – α	π + α	3π/2 – α	3π/2 + α	2π-α	2π + α

Paritatea funcțiilor trigonometrice. Unghiurile φ și -φ se formează prin rotirea fasciculului în două direcții reciproc opuse (în sensul acelor de ceasornic și în sens invers acelor de ceasornic).
Prin urmare, laturile de capăt OA 1 și OA 2 ale acestor unghiuri sunt simetrice față de axa x. Coordonatele vectorului unitar OA 1 = ( X 1 , la 1) și ОА 2 = ( X 2 , y 2) satisface relatiile: X 2 = X 1 y 2 = -la 1 Prin urmare cos(-φ) = cosφ, sin (- φ) = -sin φ, Prin urmare, sinusul este o funcție impară, iar cosinusul este o funcție pară a unghiului.
Mai departe avem:
De aceea tangenta și cotangenta sunt funcții impare ale unui unghi.

8)Funcții trigonometrice inverse - functii matematice, care sunt inverse funcțiilor trigonometrice. Funcțiile trigonometrice inverse includ de obicei șase funcții:

§ arcsinus(simbol: arcsin)

§ arc cosinus(simbol: arccos)

§ arc tangentă(desemnare: arctg; în literatura străină arctan)

§ arc tangentă(desemnare: arcctg; în literatura străină arccotan)

§ arcsecant(simbol: arcsec)

§ arccosecant(denumirea: arccosec; în literatura străină arccsc)

Numele funcției trigonometrice inverse se formează din numele funcției trigonometrice corespunzătoare prin adăugarea prefixului „ark-” (din lat. arc- arc). Acest lucru se datorează faptului că geometric valoarea funcției trigonometrice inverse poate fi asociată cu lungimea arcului unui cerc unitar (sau unghiului care subtind acest arc) corespunzător unuia sau altuia. Ocazional, în literatura străină se folosesc desemnări precum sin −1 pentru arcsinus etc.; acest lucru este considerat nejustificat, deoarece este posibilă confuzia cu ridicarea funcției la puterea lui -1.

proprietățile funcției arcsin

(funcția este ciudată). la .

la

la

Proprietățile funcției arccos[

· (funcția este simetrică central față de punctul ), este indiferentă.

·

·

·

proprietățile funcției arctg

·

· , pentru x > 0.

proprietățile funcției arcctg

(graficul funcției este simetric central față de punct

· pentru orice

·

12) Gradul unui număr a > 0 cu un exponent rațional este exponentul, al cărui exponent poate fi reprezentat ca o fracție ireductibilă obișnuită x = m / n, unde m este un număr întreg și n este un număr natural și n > 1 (x este exponentul).

Gradul cu exponent real

Să fie dat un număr pozitiv și unul arbitrar numar real. Numărul se numește grad, numărul este baza gradului, numărul este exponent.

Prin definiție se presupune:

Dacă și sunt numere pozitive și sunt numere reale, atunci următoarele proprietăți sunt adevărate:

14)Logaritmul de bază al unui număr(din grecescul λόγος - „cuvânt”, „relație” și ἀριθμός - „număr”) este definit ca un indicator al gradului în care trebuie ridicată baza pentru a obține un număr. Denumire:, pronuntat: " logaritm de bază".

Proprietățile logaritmilor:

1° - identitate logaritmică de bază.

Logaritmul unității în orice bază pozitivă, alta decât 1, este zero. Acest lucru este posibil deoarece din orice număr real poți obține 1 doar ridicându-l la puterea zero.

4° este logaritmul produsului.

Logaritmul produsului este egal cu suma logaritmilor factorilor.

5° este logaritmul coeficientului.

Logaritmul coeficientului (fracției) este egal cu diferența logaritmilor factorilor.

6° este logaritmul gradului.

Logaritmul unui grad este egal cu produsul exponentului și logaritmul bazei sale.

7°

8°

9° - trecerea la o nouă bază.

15) Număr real - (număr real), orice număr pozitiv, negativ sau zero. Prin intermediul numerelor reale se exprimă rezultatele măsurării tuturor mărimilor fizice. ;

16)unitate imaginară este de obicei un număr complex al cărui pătrat este egal cu unul negativ. Totuși, sunt posibile și alte opțiuni: în construcția dublării conform lui Cayley-Dixon sau în cadrul algebrei după Clifford.

Numere complexe(numere imaginare învechite) - numere de forma , unde și sunt numere reale, este o unitate imaginară; acesta este . Multe dintre toate numere complexe de obicei notat din lat. complex- strans legate.

Vă reamintim că în această lecție înțelegem proprietăți de grad cu indicatori naturali și zero. Gradele cu indicatori raționali și proprietățile acestora vor fi discutate în lecțiile pentru clasa a 8-a.

Un exponent cu un exponent natural are câteva proprietăți importante care vă permit să simplificați calculele în exemple de exponent.

Proprietatea #1
Produsul puterilor

Tine minte!

La înmulțirea puterilor cu aceeași bază, baza rămâne neschimbată și se adaugă exponenții.

a m a n \u003d a m + n, unde "a"- orice număr și" m","n"- orice numere întregi.

Această proprietate a puterilor afectează și produsul a trei sau mai multe puteri.

• Simplificați expresia.
  b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
• Prezentă ca diplomă.
  6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
• Prezentă ca diplomă.
  (0,8) 3 (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Important!

Vă rugăm să rețineți că în proprietatea indicată era vorba doar de înmulțirea puterilor cu aceleași temeiuri . Nu se aplică la adăugarea lor.

Nu puteți înlocui suma (3 3 + 3 2) cu 3 5 . Acest lucru este de înțeles dacă
calculați (3 3 + 3 2) = (27 + 9) = 36 și 3 5 = 243

Proprietatea #2
Diplome private

Tine minte!

La împărțirea puterilor cu aceeași bază, baza rămâne neschimbată, iar exponentul divizorului este scăzut din exponentul dividendului.

= 11 3 − 2 4 2 − 1 = 11 4 = 44

Exemplu. Rezolvați ecuația. Folosim proprietatea gradelor parțiale.
3 8: t = 3 4

T = 3 8 − 4

Răspuns: t = 3 4 = 81

Folosind proprietățile nr. 1 și nr. 2, puteți simplifica cu ușurință expresiile și efectuați calcule.

• Exemplu. Simplificați expresia.
  4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
• Exemplu. Găsiți valoarea unei expresii folosind proprietățile gradului.
  = = = 2 9 + 2

  2 5

  = 2 11

  2 5

  = 2 11 − 5 = 2 6 = 64

  Important!

  Vă rugăm să rețineți că proprietatea 2 s-a ocupat doar de împărțirea puterilor pe aceleași baze.

  Nu puteți înlocui diferența (4 3 −4 2) cu 4 1 . Acest lucru este de înțeles dacă luăm în considerare (4 3 −4 2) = (64 − 16) = 48 și 4 1 = 4

  Atenție!

  Proprietatea #3
  Exponentiație

  Tine minte!

  Când ridicați o putere la o putere, baza puterii rămâne neschimbată, iar exponenții sunt înmulțiți.

  (a n) m \u003d a n m, unde „a” este orice număr și „m”, „n” sunt orice numere naturale.

  
  

  Proprietăți 4
  Gradul de produs

  Tine minte!

  Când ridicați un produs la o putere, fiecare dintre factori este ridicat la o putere. Rezultatele sunt apoi multiplicate.

  (a b) n \u003d a n b n, unde „a”, „b” sunt orice numere raționale; "n" - orice număr natural.

  • Exemplul 1
    (6 a 2 b 3 c) 2 = 6 2 a 2 2 b 3 2 s 1 2 = 36 a 4 b 6 s 2
    
  • Exemplul 2
    (−x 2 y) 6 = ((−1) 6 x 2 6 y 1 6) = x 12 y 6

  Important!

  Vă rugăm să rețineți că proprietatea nr. 4, ca și alte proprietăți ale gradelor, se aplică și în ordine inversă.

  (a n b n)= (a b) n

  Adică, pentru a înmulți grade cu aceiași exponenți, puteți înmulți bazele și lăsați exponentul neschimbat.

  • Exemplu. Calculati.
    2 4 5 4 = (2 5) 4 = 10 4 = 10.000
  • Exemplu. Calculati.
    0,5 16 2 16 = (0,5 2) 16 = 1

  În mai mult exemple dificile pot exista cazuri când înmulțirea și împărțirea trebuie efectuate peste puteri cu temeiuri diferiteși diferiți indicatori. În acest caz, vă sfătuim să faceți următoarele.

  De exemplu, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216
  

  Exemplu de exponențiere a unei fracții zecimale.

  4 21 (−0,25) 20 = 4 4 20 (−0,25) 20 = 4 (4 (−0,25)) 20 = 4 (−1) 20 = 4 1 = patru

  Proprietăți 5
  Puterea coeficientului (fracțiilor)

  Tine minte!

  Pentru a crește un coeficient la o putere, puteți crește dividendul și divizorul separat la această putere și puteți împărți primul rezultat la al doilea.

  (a: b) n \u003d a n: b n, unde "a", "b" sunt orice numere raționale, b ≠ 0, n este orice număr natural.

  • Exemplu. Exprimați expresia ca puteri parțiale.
    (5: 3) 12 = 5 12: 3 12

  Vă reamintim că un coeficient poate fi reprezentat ca o fracție. Prin urmare, ne vom opri asupra subiectului ridicării unei fracții la o putere mai detaliat pe pagina următoare.

Subiectul lecției: Grad cu exponenți raționali și reali.

Obiective:

Educational :

• generalizarea conceptului de grad;

  să dezvolte capacitatea de a găsi valoarea diplomei cu un indicator real;

  consolidarea capacității de a utiliza proprietățile gradului la simplificarea expresiilor;

  dezvolta deprinderea de a utiliza proprietăţile gradului în calcule.

Educational :

• dezvoltarea intelectuală, emoțională, personală a elevului;

  dezvoltarea capacității de generalizare, sistematizare pe bază de comparație, tragerea unei concluzii;

  activarea activității independente;

  dezvolta curiozitatea.

Educational :

• educaţia comunicativă şi cultura informaţiei elevi;

  educația estetică se realizează prin formarea capacității de a întocmi rațional, precis o sarcină pe o tablă și într-un caiet.

Elevii ar trebui să știe: definiție și proprietăți ale gradului cu exponent real

Elevii ar trebui să fie capabili să:

determinați dacă o expresie cu un grad are sens;

utilizați proprietățile gradului în calcule și simplificare a expresiilor;

rezolva exemple care conțin o diplomă;

comparați, găsiți asemănări și diferențe.

Formularul lecției: seminar - atelier, cu elemente de cercetare. Suport computer.

Forma de organizare a instruirii: individual, grup.

Tehnologii pedagogice : învăţare bazată pe probleme, învăţare colaborativă, personal - învăţare orientată, comunicativ.

Tip de lecție: lectie de cercetare si munca practica.

Imaginile vizuale ale lecției și fișele:

prezentare

formule și tabele (aplicația 1.2)

sarcina pentru muncă independentă (Anexa 3)

Planul lecției

№

Etapa lecției

Scopul scenei

Timp, min.

Începutul lecției

Raportarea subiectului lecției, stabilirea scopurilor lecției.

1-2 min

munca orală

Examinați formulele de putere.

Proprietăți de grad.

4-5 min.

Soluție frontală

planșe din manualul nr. 57 (1,3,5)

№58(1,3,5) cu respectarea detaliată a planului de soluționare.

Formarea deprinderilor și abilităților

cere elevilor să aplice proprietăți

grade la găsirea valorilor expresiei.

8-10 min.

Lucrați în microgrupuri.

Identificarea lacunelor în cunoștințe

elevilor, creând condiţii pentru

dezvoltarea individuală student

pe lecție.

15-20 min.

Rezumând munca.

Urmăriți succesul muncii dvs

Elevii la decizie independentă sarcini pe subiect, aflați

natura dificultăților, cauzele acestora,

oferi soluții colective.

5-6 min.

Teme pentru acasă

Introduceți elevii temele. Dați explicațiile necesare.

1-2 min.

ÎN CURILE CURĂRILOR

Organizarea timpului

Buna baieti! Scrieți în caiete numărul, tema lecției.

Se spune că inventatorul șahului, drept recompensă pentru invenția sa, i-a cerut raja niște orez: el a cerut să pună un bob pe prima celulă a tablei, pe a doua - de 2 ori mai mult, adică 2 boabe, pe tabla. a treia - încă de 2 ori mai mult, adică 4 boabe etc. până la 64 de celule.

Cererea lui i s-a părut prea modestă pentru Raja, dar curând a devenit clar că era imposibil să o îndeplinească. Numărul de boabe care trebuiau oferite inventatorului șahului drept recompensă este exprimat prin suma

1+2+2 2 +2 3 +…+2 63 .

Această sumă este egală cu un număr mare

18446744073709551615

Și este atât de mare încât această cantitate de cereale ar putea acoperi întreaga suprafață a planetei noastre, inclusiv oceanul mondial, cu un strat de 1 cm.

Gradele sunt folosite la scrierea numerelor și a expresiilor, ceea ce le face mai compacte și mai convenabile pentru efectuarea acțiunilor.

Adesea, gradele sunt folosite la măsurarea cantităților fizice, care pot fi „foarte mari” și „foarte mici”.

Masa Pământului 600000000000000000000t se scrie ca produs de 6,10 21 t

Diametrul unei molecule de apă 0,0000000003 m este scris ca produs

3.10 -10 m.

1. Ce concept matematic este asociat cu cuvintele:

Baza
Index(grad)

Ce cuvinte pot combina cuvintele:
Numar rational
Întreg
Numar natural
număr irațional(Numar real)
Formulați subiectul lecției.(Putere cu exponent real)

2. Deci a X,Undex este un număr real. Selectați dintre expresii

Cu indicator natural

Cu un număr întreg

cu exponent rațional

Cu un exponent irațional

3. Care este scopul nostru?(UTILIZARE)
Ce felobiectivele lecției noastre ?
- Generalizarea conceptului de grad.

Sarcini:

– repetați proprietățile gradului
– luați în considerare utilizarea proprietăților gradului în calcule și simplificări ale expresiilor
– dezvoltarea abilităților de calcul

4 . Gradul cu exponent rațional

Baza

grad

Gradul cu exponentr, baza a (nN, mn

r= n

r= - n

r= 0

r= 0

r=0

A n= A. A. … . A

A -n=

A 0 =1

A n=a.a. ….A

A -n=

Nu exista

Nu exista

A 0 =1

a=0

0 n=0

Nu exista

Nu exista

Nu exista

5 . Dintre aceste expresii, alege-le pe cele care nu au sens:

6 . Definiție

Dacă numărulr- firesc, atunci rexistă o lucrarernumere, fiecare dintre ele egal cu a:

A r= A. A. … . A

Dacă numărulr- fracționat și pozitiv, adică undemșin- naturală

numere, atunci

Dacă indicatorulreste rațional și negativ, apoi expresiaA r

este definit ca reciproca aA - r

sau

În cazul în care un

7 . De exemplu

8 . Puterile numerelor pozitive au următoarele proprietăți de bază:

9 . calculati

10. Ce acțiuni (operații matematice) pot fi efectuate cu grade?

Meci set:

A) La înmulțirea puterilor cu baze egale

1) Bazele se înmulțesc, dar exponentul rămâne același

B) La împărțirea gradelor cu baze egale

2) Bazele sunt împărțite, dar exponentul rămâne același

B) La ridicarea unei puteri la o putere

3) Baza rămâne aceeași, dar exponenții sunt înmulțiți

D) La înmulțirea puterilor cu exponenți egali

4) Baza rămâne aceeași, iar exponenții se scad

E) La împărțirea gradelor cu indicatori egali

5) Baza rămâne aceeași, iar indicatorii se adună

11 . Din manual (la tablă)

Pentru o soluție de clasă:

№57 (1,3,5)

№58 (1, 3, 5)

№59 (1, 3)

№60 (1,3)

12 . De UTILIZAȚI materiale

(muncă independentă) pe pliante

XIVsecol.

Răspuns: Oresma. 13. În plus (individual) pentru cei care pot îndeplini sarcinile mai repede:

14. Teme pentru acasă

§ 5 (cunoașteți definiții, formule)

№57 (2, 4, 6)

№58 (2,4)

№59 (2,4)

№60 (2,4) .

La sfârșitul lecției:

„Matematica deja trebuie predată atunci, că pune mintea în ordine”

– Așa a spus marele matematician rus Mihail Lomonosov.

- Mulțumesc pentru lecție!

Atasamentul 1

1. Grade. Proprietăți de bază

indicator

a 1 =a

A n=a.a. ….A

aRn

3 5 =3 . 3 . 3 . 3 . 3 . 3=243,

(-2) 3 =(-2) . (-2) . (-2)= - 8

Gradul cu exponent întreg

a 0 = 1,

unde un

0 0 - nedefinit.

Grad cu rațional

indicator

UndeA

m n

Gradul cu exponent irațional

Răspuns: ==25,9...

1. A X. A y=a x+y

2.a X: A y==a X y

3. .(A X) y=a X y

4.(a.b) n=a n.b n

5. (=

6. (

Anexa 2

2. Gradul cu exponent rațional

Baza

grad

Gradul cu exponentr, baza a (nN, mn

r= n

r= - n

r= 0

r= 0

r=0

A n= A. A. … . A

A -n=

A 0 =1

A n=a.a. ….A

A -n=

Nu exista

Nu exista

A 0 =1

a=0

0 n=0

Nu exista

Nu exista

Nu exista

Anexa 3

3. Muncă independentă

Pentru prima dată, acțiunile asupra puterilor au fost folosite de un matematician francezXIVsecol.

Descifrează numele omului de știință francez.